1.1. Комплексные числа (кч)

Комплексным числом z называется выражение z = a+bi, где , i – мнимая единица. i ² = –1.

a – действительная часть КЧ или a = Re z.

b – мнимая часть КЧ или b = Im z.

0+bi = bi - чисто мнимое число

a + 0i = a - действительное число

0 + 1i = i	1 + 0i = 1	0 + 0i = 0
мнимая единица	обычная единица	обычный нуль

Z₁ = a₁ + b₁i

Z₂ = a₂ + b₂i

Действия над КЧ.

Z₁ Z₂ = (a₁ a₂) + (b₁ b₂) i – сложение/вычитание КЧ.

Возведение в степень мнимой единицы:

i¹ = i i² = – 1 i³ = i i⁴ = 1

Z₁ Z₂ = (a₁ + b₁ i) (a₂ + b₂ i) = a₁ a₂ + a₁ b₂ i + a₂ b₁ i + b₁ b₂ i² =

= (a₁ a₂ – b₁ b₂) + (a₁ b₂ + a₂ b₁) i – произведение КЧ.

Сопряженным числом ( ) для данного комплексного числа называется число, которое отличается только знаком мнимой части от данного числа.

Пример:

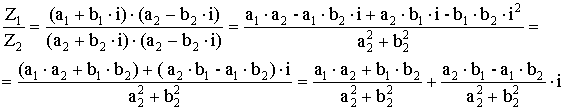  – деление КЧ.

Пример:

Комплексная плоскость.

Z = a + bi – алгебраическая форма записи КЧ.

Модуль КЧ.

Аргумент КЧ.

Аргумент КЧ – .

Полярная система координат

Декартова система.        Полярная система.

– полярный радиус, – полярный угол, – полярные координаты.

; 

Пример:

– тригонометрическая форма записи КЧ.

Примеры:

Формула Эйлера.

– Формула Эйлера

– взаимосвязь между e, i и

– показательная форма КЧ.

КЧ не сравнивают между собой. Множество КЧ не упорядоченно.

Возведение в степень КЧ.

При возведении в степень модуль возводиться в эту степень, а аргумент умножается на показатель степени.

Формула Муавра.

Возведение во 2 – ю и 3 – ю степень по формуле Муавра:

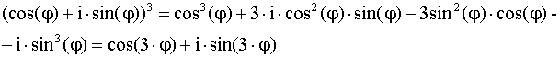
Используя равенство КЧ, получим: s

Извлечение корня из КЧ.

k = 0, 1…,n – 1.

Корень n – ой степени из КЧ имеет n различных значений.

Примеры:

1. 

2. 

Все корни n-ой степени из единицы находятся на единичной окружности и делят эту окружность на n равных частей.

1.2. Функция, способы её задания, простейшие свойства.

Основные обозначения:

N – натуральные числа,

Q – рациональные(дробные),

Z – целые числа,

R – действительные числа;

Счетное множество – это множество, элементы которого можно пересчитать.

– счетные и имеют одинаковую мощность

R – несчетное множество.

Множество действительных чисел всюду плотно на числовой оси.

[a, b] – замкнутый интервал,   (a, b) – открытый интервал

Окр [x₀] – окрестность точки x₀ , любой открытый интервал, содержащий x₀.

Окр [x₀] = (a, b), где (a, b) содержит x₀ – это окрестность.

ax₀ = x₀b, – окрестность x₀

Кванторы

1) – кванты всеобщности;

2) – кванты существования.

|x – x₀| – расстояние от точки x до точки x₀

Числовой функцией называется соответствие между числовыми множествами X Y, при котором каждому значению x соответствует (сопоставлено) некоторое значение y.

У каждого прообраза всегда один образ, у каждого образа может быть много прообразов.

Взаимнооднозначная функция – это когда разные x имеют разные y.

Способы задания функций:

а) аналитический;

б) графический;

в) табличный;

г) алгоритмический.

Функции делятся на 2 класса

1. Элементарные

2. Неэлементарные (специальные).

Элементарные функции изучаются в школьной математике и делятся на:

1. Основные элементарные функции

а) степенные y = xⁿ

б) показательные y = a^x

в) тригонометрические y = sin x и другие.

2. Элементарные, полученные из основных с помощью арифметических операций и операции получения сложной функции (операции композиции).

f

X          Y         

f ^-1 (обратная функция)

Обратные к показательным функциям – логарифмические функции. Обратные к тригонометрическим

Пример:

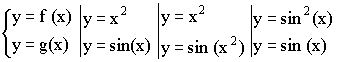
y = f (g(x)) – сложная функция – композиция элементарных функций.

Элементарными функциями называются функции, полученные из элементарных базисных функций с помощью алгебраических операций и операций композиции.

Г(f) – график функции. График функции есть множество точек (x, y), где y = f(x).

Общие свойства функций:

1. Четность –

2. Нечетность –

3. Периодичность –

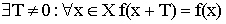
Рисунок

f(x) – ограниченная сверху, если

f(x) – ограниченная снизу, если

f(x) – ограниченная, если

f(x) – монотонная, если она постоянно возрастает или постоянно убывает

Если y = f(x), то Д – область определения данной функции.

Свойства модулей суммы и разности:

1. 

2.