Линейка и Анал. Геометрия.

Понятие числовой матрицы

Числовая матрица – прямоугольная таблица чисел, состоящая из строк и столбцов. Размеры матрицы обозначаются M * N, где M-число строк, N-число столбцов.

Пример:

A= или A=

Общее обозначение:

A= или A=

, где - элемент матрицы, находящийся на пересечении i-ой строки и j-ого столбца:

Если M=N, то матрица называется квадратной. В этом случае

N – ее порядок . В квадратной матрице выделяются две диогонали –главная и побочная:

. .           . .

. . главная . . . побочная

. .           . .

Пример:

A = главную диогональ образуют эл-ты:

, а побочную

Определители второго порядка.

Пусть дана матрица второго порядка A= .

Определителем второго порядка называется число, вычисляемое по правилу:

Определитель второго порядка равен произведению элементов

Главной диогонали минус произведение элементов Побочной дио-

гонали.

= 1*(-4)-6 = -10

Подматрица, минор, алгебраическое дополнение.

Пусть дана какая-либо матрица (например, порядка 3):

А=

Подматрицей матрицы А называется часть этой матрицы, полученная вычеркиванием какого-либо количества строк, и(или) какого-либо количества столбцов.

Например, если вычеркнуть первую строку и второй столбец ,то получим подматрицу даной матрицы:

Минором элемента определителя называется определитель, полученный вычеркиванием i-ой строки и j-ого столбца.

Алгебраическим дополнением элемента называется минор, взятый со знаком “+” или “ ” в зависимости от места этого элемента в определителе.

Обозначение: =

Если i+j - четное число , то знак алгебраического дополнения

и минора одинаковы, если нечетное , то их знаки противоположны.

Символически покажем положительные и отрицательные места в определителе:

или

ОПРЕДЕЛИТЕЛИ ТРЕТЬЕГО ПОРЯДКА.

Определителем третьего порядка называется число, вычисляемое по правилу:

= =

Определитель третьего порядка равен сумме произведений элементов первой строки на их алгебраические дополнения.

Заменим алгебраические дополнения на миноры:

=

= - +

Вычисляя миноры, получим:

=

СВОЙСТВА ОПРЕДЕЛИТЕЛЕЙ.

Свойство 1.

При замене строк на столбцы определитель не меняется.

=

(такая операция называется транспонированием).

Следствие: строки и столбцы равноправны ,т.е любые свойства или утверждения относительно строк справедливы и для столбцов и наоборот.

Свойство 2.

При перестановке двух строк определитель меняет знак

на противоположный.

= 

Следствие: любую строку (столбец ) можно поставить первой (первым)

Свойство 3.

Определитель с двумя равными строками равен нулю.

= 0

Свойство 4.

Общий множитель элементов строки можно выносить за знак определителя.

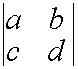
Следствие :

Постоянный множитель можно внести в какую-нибудь строку

Свойство 5.

Если элементы какой –либо строки состоят из двух слагаемых,

то определитель можно представить в виде суммы двух определите-

лей.

Свойство 6.

Определитель не меняется ,если любую строку умножить на любое

число и прибавить к любой другой строке.

Случаи ,когда определитель равен нулю:

1. Все элементы какой-либо строки равны нулю

2. Две строки одинаковы

3. Элементы двух строк пропорциональны

ОПРЕДЕЛИТЕЛИ ПОРЯДКА n.

Вычисление определителей порядка n.

Для вычисления порядка n используется метод разложения по cтроке.

Алгебраическое дополнение получается вычеркиванием i-строки

и j-столбца. Этот процесс мы будем продолжать до тех пор пока

не получим определители порядка 2 или 3

Формулу (1) используют как правило при i=1

Пример:

Понятие системы линейных уравнений.

Система линейных уравнений порядка n имеет вид:

При этом числа -называются коэфициентами при неизвестных

-свободные члены

Матрица называется матрицей системы

Числа - решение системы,если при подстановке этих чисел в систему каждое из уравнений системы превращается в верное числовое тождество.

Система линейных уравнений называется совместной, если она имеет по крайней мере одно решение.

Если система линейных уравнений не имеет решений , то система называется несовместной.

Формулы Крамера

Расмотрим систему уравнений (*). И пусть А- матрица системы

Если i –столбец заменим свободными членами , то соответствующую матрицу обозначим

Если система линейных уравнений (*) такова, что определитель

системы отличен от нуля ,то система линейных уравнений имеет

единственое решение , которое находится по формуле:

Две матрицы A и B называются равными ,если они имеют

один и тот же порядок и если элементы стоящие на соответствующих местах равны.

К линейным операциям относятся :

Умножение матрицы на число

Для того чтобы умножить матрицу на число нужно каждый элемент

матрицы умножить на это число:

Сложение матриц.

Складывать можно только матрицы одинаковых размеров:

Свойства линейных операций

Если матрица в качестве элементов имеет нули , то такая матрица называется нулевой.

Произведение матриц .

Пример:

. = =

. =

.

Если для матриц А и В выполняется равенство А* В=В*А ,то

матрицы называются перестановочными.

Если для матриц А , В , С имеет смысл операция произведения,

то выполняются равенства

A(B*C)=(A*B)*C

A(B+C)=AB+AC

(B+C)A=BA+CA

Транспонирование матриц

Рассмотрим матрицы

A^T называется транспонированной по отношению к A

Если A_T получена из матрицы А заменой строк на столбцы то

назавают главной диагональю

Очевидно:

Если А является квадратной матрицей(n*n), то элементы матрицы

Если для квадратной матрицы выполняется условие

то матрица А называется симметричной и в этом случае достаточно указать элементы, стоящие на главной диагонали и элементы, стоящие над главной диагональю.

Понятие обратной матрицы.

Обратные матрицы существуют только для квадратных матриц. Квадратная матрица ,у которой на главной диагонали стоят

единицы, а вне главной диагонали - нули, называется единичной матрицей.

Например, единичная матрица второго порядка:

Теорема.

Если А и В – квадратные матрицы одного и того же порядка n, то определитель их произведения равен произведению определителей матриц-сомножителей:

Определение обратной матрицы:

Матрица В называется обратной для матрицы А , если А и В перестановочны и А*В=В*А=Е

Обозначение обратной матрицы:

Теорема.

Если матрица А имеет обратную ,то ее определитель отличен от

нуля.

Доказательство.

Так как А имеет обратную матрицу, то

Воспользуемся теоремой о том ,что определитель произведения

равен произведению определителей.

что и требовалось доказать.

Нахождение обратной матрицы методом Крамера

Теорема.

Если квадратная матрица А имеет определитель отличный от нуля, то данная матрица имеет обратную.

Доказательство.

Пусть матрица А такова, что её определитель отличен от нуля.

Докажем, что существует матрица В, такая что:

* =

 

Отсюда, в частности, следует:

Система (3) –из трех уравнений с тремя неизвестными, и т.к. определитель системы (3) по условию отличен от нуля , то эту систему можно решить методом Крамера причем решение (3) - единственно.

Аналогично можно доказать существование и единственность всех остальных элементов матрицы В.

Алгоритм нахождения обратной матрицы методом Крамера.

Первоначально находим определитель матрицы А и если он

равен нулю , то обратной матрицы не существует.

Если определитель отличен от нуля , то находим союзную

матрицу

состоящую из алгебраических дополнений элементов матрицы А.

Элементарные преобразования матриц.

Эквивалентные матрицы.

К элементарным преобразованиям относятся:

1. умножение любой строки матрицы на число , отличное от нуля;

пример

=

2. к любой строке можно добавить любую другую строку , умноженую на любое число;

3. перестановка двух строк.

Матрицы, полученные с помощью элементарных преобразований

называются эквивалентными

А В , В С , А С

Вычисление обратной матрицы с помощью элементарных преобразований.

Расмотрим квадратную матрицу А и предположим , что

тогда используя элементарные преобразования эту матрицу

можно привести к единичной матрице .Таким образом единичная

матрица эквивалентна любой невырожденой матрице того же

порядка.

Теорема

Если элементарные преобразования:

переводят невырожденую матрицу А в единичную , то

те же самые преобразования, взятые в том же порядке, переводят

единичную матрицу в обратную для A.

Доказательство:

отсюда

Системы линейных уравнений.

Основные понятия.

Система уравнений вида:

называется линейной системой из n уравнений с m неизвестными.

(a_ij) коэффициенты при неизвестных x₁, x₂,...,x_m

b₁,b₂,...,b_n - свободные члены

Матрица А системы (*) состоит из коэффициентов a_ij, размера n*m .

Если неизвестные и свободные члены представим в виде: ,

то систему уравнений (*) мы можем переписать в виде: (3)

Запись системы в виде (3) называют матричной формой записи системы линейных уравнений (*) .Следует особо обратить внимание на то, что m может быть неравно n . Если m=n и матрица А является невырожденой , то из соотношения (3) вытекает: (4)

Равенство (4) получается умножением (3) слева на А-1. Система (*) называется совместной, если она имеет по крайней мере одно решение. В противном случае система называется несовместной. Решить систему - означает найти все её решения.

Метод Гаусса

Расмотрим систему (*):

Припишем к матрице А матрицу-столбец В

Припишем к матрице А матрицу-столбец В:

Матрица H называется расширенной матрицей системы. Матрица, у которой ниже главной диагонали стоят нули называется треугольной.Метод Гаусса (метод исключения неизвестных) состоит в том, что расширенную матрицу системы с помощью элементарных преобразований мы приводим к треугольному виду. Если у нас при этом получается матрица вида: 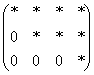то, система решений не имеет.

Если треугольная матрица получается вида: ,то система имеет бесконечно много решений. При этом какие-то неизвестные обьявляются свободными, а остальные неизвестные могут быть выражены через них. Свободные неизвестные могут принимать любые значения. Если матрица примет вид: ,то этом случае система имеет единственное решение.

Пример:

Элементарные преобразования расширенной матрицы системы, приводящие её к треугольному виду, могут быть такими:

~ ~

В итоге получим систему:

Откуда получим значения неизвестных: y = -7,25 x = 2,875

Пример:

~ ~ ~

Рассмотрим систему линейных уравнений.

Задача: определить:

1. Совместна или нет данная система

2. Если совместна, то сколько имеет решений а)единственное

б)беск.множество

Понятие ранга матрицы

А=( ) i= j=

Возьмем в матрице К строк и К столбцов, тогда элементы матрицы, стоящие на пересечении этих строк и столбцов образуют квадратную матрицу порядка К. Определитель этой квадратной матрицы называется минором порядка К для матрицы А.

Опр.1. Наибольший порядок минора матрицы, отличный от нуля называется рангом матрицы.

Опр.2. Число r(A)=k называется рангом матрицы А, если среди миноров порядка k есть по крайней мере один, отличный от нуля, а все миноры большего порядка равны нулю.

М= =0 М= =-2 0 М= =0 М= =3 Ранг равен 3.

Совершенно очевидно, что нулевой ранг имеет только нулевая матрица. Если матрица не нулевая то её ранг 1. С другой стороны если матрица имеет порядок MxN, то r(A) min(M,N).

Теоремы о ранге матриц

Т.1. Если матрица А эквивалентна матрице B, то ранг матрицы А равен рангу матрицы B (элементарные преобразования не изменяют ранга матрицы).

Доказательство. Для докозательства достаточно доказать, что каждое из преобразований не может изменить ранга матрицы.

1) А~B B получена умножением строки(столбца) на отличное от нуля число.

А= B=

Если i-я строка не входит в выделенный минор то миноры матриц А и B совпадают. Если i-я строка входит в выделенный минор В= А(по св-ву определителей). Если минор А был отличен от нуля, то В будет отличен от нуля. Таким образом умножение на отличное от нуля число не изменяет ранг матрицы.

2) A~B B получена прибавлением строк

А= В=

 

Если выбранные строки не содержат i-й строки, то соответствующие миноры матриц А и В полностью совпадают. Если минор матрицы А=0, то и минор матрицы В=0, если минор матрицы А 0, то и минор матрицы В 0.

Если выбранные миноры содержат i-ю и j-ю строки, тогда М(А)= А=

В=

минор В получен из А путем прибавления строки.

3. Элементарные преобразования получаются с помощью конечного числа преобразований 1 и 2 типа и по уже доказанному на каждом из шагов ранг матрицы не меняется. Следовательно, он не изменится и за конечное число шагов. Ранг матрицы не меняется, если произведено конечное число элементарных преобразований.

Т.2. Ранг ступенчатой матрицы равен числу ее ненулевых строк.

Вычисление ранга матрицы

Используя утверждение доказанной теоремы, легко вычислить ранг матрицы

1. с помощью элементарных преобразований матрица приводится к ступенчатому виду.

2. Считается число ненулевых строк ступенчатой матрицы

Ясно, что если матрица является квадратной и невырожденной, то её ранг равен порядку этой матрицы.

ПРИМЕР

~ ~

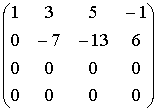
Ответ: r(A)=2

Исследование систем линейных уравнений. Теорема Кронекера-Капелли.

Рассмотрим систему линейных уравнений

(*)

А=( ) H=

Т. Кронекера-Капелли.

Система ур-ний (*) совместна тогда и только тогда, когда ранг матрицы системы А равен рангу расширенной матрицы r(A)=r(H)

Если система совместна, то она имеет единственное решение, если r(A)=r(H)=n и его можно найти методами Крамера или Гаусса.

Если r(A)=r(H)=k<n, то система имеет бесконечно много решений. В этом случае n-k неизвестных обьявляются свободными неизвестными (принимают любые значения), оставшиеся k неизвестных выражаются через эти свободные неизвестные.

 

Однородные системы линейных уравнений

Если в системе (*) все свободные члены равны нулю, то такая система является однородной.

Однородные системы всегда совместны т.к. = = = =0 всегда является решением. Такое решение называется тривиальным.

1) то

2) Если ранг матрицы А меньше числа неизвестных,то система имеет бесконечно много решений

Свойства решений линейной однородной системы уравнений.

1) Если является решением системы, то также является решением.

Доказательство.

2) Если является решением системы

также является решением той же самой системы, то и

также является решением системы

Доказательство.

+

откуда получим

3) Если и два различных решения системы, то их линейная комбинация, равная

также является решением системы.

Доказательство.

+

откуда получим

Каждое из решений системы можно записать в виде строки

матрицы , тогда на основании свойств можно утверждать, что матрицы есть решения, то также являются решением. Минимальная возможная система решений через которую выражаются все остальные решения называется фундаментальной системой решений.

Пример.

~ ~

{ {

{ {

Геометрический вектор

Понятие вектора

Вектор: отрезок с началом в точке А и концом в точке В.

Обозначается:

Два вектора равны, если они совпадают при параллельном переносе.

Два вектора называются коллинеарными, если они параллельны.

Три вектора называются компланарными, если они лежат в одной плоскости.

Линейные операции над векторами.

А) Умножение вектора на число.

Б) Сложение векторов

1)

2)

3) -длину вектора умножить на и оставить направление вектора если

Таким образом операции обладают св-ми.

1)

2)

Вектор у которого начало и конец совпадают есть нулевой вектор

3)

4)

5)

6)

7)

8)

Вычитание- обратное сложению.

Линейная зависимость векторов,теоремы о линейной зависимости.

Опр 1. Система векторов называется линейно зависимой, если сущ. числа не все равные 0, такие что (1)

Система векторов называется линейно независимой, если равенство (1) возможно только в том случае, когда все числа =0

Выражение стоящее в левой части рав-ва (1) наз-ют линейной комбинацией векторов

Опр 2. Система векторов является линейно зависимой, если существует линейная комбинация этих векторов с неравными 0 числами, которая тождественно равна.

Теор 1. Если система векторов содержит нулевой вектор, то данная система линейно зависима.

Док-во. Пусть , тогда

Теор 2. Если к системе линейно зависимых векторов добавить произвольный вектор , то вновь полученная система будет линейно зависима.

Док-во. Т.К. система векторов линейно зависима, то есть не все равные нулю, такие что (2) (3)

(4)

Есть ,

0 -не все равны нулю

Следовательно система линейно зависима.

Следствие. Если к линейно зависимой системе добавить любое кол-во векторов, то полученная система будет линейно зависима.

Теор. (О линейной зависимости двух векторов.)

Два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.

Док-во.

-коллинеарны

Теор. Три вектора линейно зависимы тогда и только тогда, когда они компланарны

Док-во.

Для и пл-ть , что (или //) и либо , либо // ей они компланарны.

Теор. В трехмерном пространстве любые 4 вектора линейно зависимы.

Док-во.

-угол между

Вектор в системе координат

Базис-максимальная упорядоченная

система линейно независимых векторов.

На плоскости 2 любых неколлинеарных вектора образуют базис.

ДПБ-базис, состоящий из ортогональных еденичных векторов.

Операции над векторами в координатной форме.

-нач.точка -кон.точка

направляющие косинусы

Скалярное произведение векторов

Опр. Скалярным произведением векторов наз-ся скалярное произведение длин этих векторов на косинус угла между ними.

Если вектор нулевой, то все произведения-ноль

Св-ва скалярного произведения.

1. Если и ортоганальны , то

2. если ; если

3. (коммутативность)

4. (дистрибутивность)

5. 

6. = =

( скалярное произведение в координатах)

Условие ортоганальности векторов

Условие коллинеарности векторов

Скалярный квадрат

 

Векторное произведение векторов.

Ориентация базиса

Декартов прямоугольный

базис на плоскости

Декартов прямоугольный

базис в пространстве

Правой тройкой векторов называется такая тройка, что если смотреть с конца вектора , то поворот от происходит в положительном направлении (против часовой стрелки).

Опр: Векторным произведением, 2-х векторов называется вектор , такой что

1) -правая тройка

2)

3)

Свойства векторного произведения.

1. Если 2 вектора коллиниарны , их произведение =0

2. Если поменять местами сомножители, меняется знак

(антикоммутативность)

3. 

4. 

5. 

Пример.

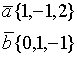
Смешанное произведение векторов.

= = =

Свойства смешанного произведения.