25.Ортогональные и косоугольные аксонометрические проекции

В зависимости от направления проецирования S по отношению к плоскости проекций П' аксонометрические проекции подразделяются на:

ортогональные (когда проецирующие лучи направлены перпендикулярно к П');

косоугольные (когда проецирующие лучи направлены к П' под углом отличным от 90˚).

Для построения аксонометрической проекции точки А необходимо построить координатную ломаную линию. Аксонометрические ZA.YA; Z'=WXA; Y'A=Vкоординаты точки будут равны: X'A=U

17.1 Основное предложение аксонометрии

При построении параллельной аксонометрической проекции можно произвольно выбрать плоскость проекций П' и направление проецирования.

Любому изменению взаимного положения осей координат и плоскости проекций (или изменению направления проецирования) будет соответствовать как изменение положения аксонометрических осей, так и коэффициентов искажения по этим осям.

Между коэффициентами искажения и углом проецирования существует следующая зависимость:

UІ+VІ+WІ=2+ctg  (теорема Польке)

- угол между направлением проецированиягде:  и плоскостью проекций.

= 90° (ортогональная аксонометрическаяПри проекция):

UІ+VІ+WІ=2

17.2 Свойства ортогональной аксонометрической проекции

Наибольшее применение в практике получили прямоугольные аксонометрические проекции, которые обладают большей наглядностью и упрощениями, которые в них достигаются. Свойств этих три. Нам сейчас важно запомнить одно:

 коэффициенты искажения в ортогональной аксонометрии равны косинусам углов наклона натуральных осей к плоскости проекций

Все три коэффициента искажения ограничены поэтому крайними значениями 0 и 1.

СТАНДАРТНЫЕ АКСОНОМЕТРИЧЕСКИЕ ПРОЕКЦИИ

ГОСТ 2.317-69 предусматривает три частных вида аксонометрических проекций.

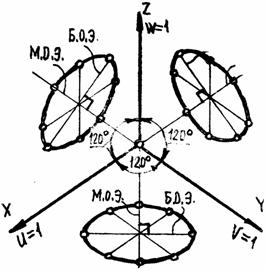
18.1 Прямоугольная изометрия

Аксонометрические оси в пря- моугольной изометрии образуют между собой углы 120°. Коэффициенты искажения по аксонометрическим осям (рисунок 6-2) U=V=W.

=Cos=CosОтсюда Cos .==и

Это означает, что натуральные координатные 0,82.оси одинаково наклонены к плоскости проекций, тогда: UІ=VІ=WІ откуда 3UІ=2 и U

Рисунок 6-2

На практике пользуются приведенной прямоугольной изометрией, в которой показатели искажения приводятся к единице, т.е.U=V=W=1. Коэффициент приведения m=U/u=1,0/0,82=1,22,. Аксонометрическое изображение будет увеличено в 1.22 раза относительно оригинала.

МА=1,22:1. При U=V=W=0.82 м.о.э.=0,58d, Б.О.Э.=d.

  При U=V=W=1,0 м.о.э.=0,71d, Б.О.Э.=1,22d.

18.2 Прямоугольная диметрия

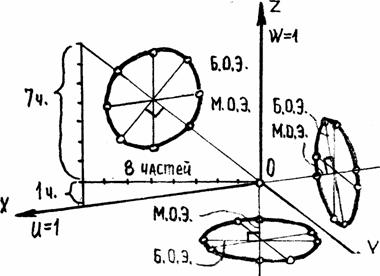
Эта проекция представлена на рисунке 6-3. Здесь W, V=U/2.U=W; V

Тогда UІ+UІ/4+UІ=2 откуда U=W=0.94, V=0.47.

При приведении коэффициентов к единице (округлении):

U=W=1.0, V=0.5 получим аксонометрическое изображение увеличенным в m=1/0.94=1.06 раза. МА=1.06:1.

При U=W=1 и V=0.5 м.о.э. = 0.35d; Б.О.Э. = 1.06d для координатных плоскостей ХОУ и YOZ, а для координатной плоскости ХOZ: м.о.э. = 0.95d, Б.О.Э. = 1.06d.

18.3 Косоугольная фронтальная диметрия

В практике встречаются случаи, когда целесообразно сохранить неискаженными фигуры расположенные в плоскостях, параллельных фронтальной плоскости проекций (например, при изображении технической детали, имеющей много окружностей в параллельных плоскостях). Эти детали проще изобразить, если окружности будут проецироваться в аксонометрии без искажения.

Для получения такой аксонометрической проекции плоскость проекций П' располагают параллельно координатной плоскости ХОZ. Тогда оси координат Х и Z, параллельные П', проецируются на неё в натуральную величину, и коэффициенты искажения U=W=1. Коэффициент искажения по оси Y будет равен:

 откуда VІ=ctg UІ+VІ+WІ=2+ctg

где -угол между направлением проецирования и плоскостью проекций П'.

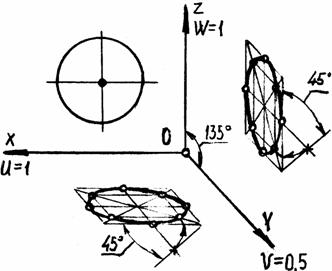
На практике направление оси Y выбирают таким образом, чтобы углы образованные аксонометрической осью Y с осями Х и Z- равнялись 135°, а показатель искажения V=0.5 (рисунок 6-4).