6, Производная функция одной переменной. Определение, геометрический смысл, простейшее правило вычисления производной. Производная сложной функции. Формула Тейлора.

Пусть функция определена на интервале . - приращение аргумента. .

.

Рассмотрим предел . Если этот предел существует и конечен, то функция называется дифференцируемой в точке х, а значение предела называется производной от этой функции: .

П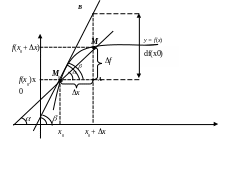 равая производная: . Левая производная: .

Определение: Проведем секущую к графику функции через точку М0(х0, f(x0)) и . Угол между секущей и положительным направлением оси х обозначим через . Предельное положение секущей при , если оно существует называется касательной к кривой в точке М0. угол между касательной и осью х обозначим через .

Из треугольника М0МА следует, что угол , тогда предел . (касательная будет стремиться к секущей).

С геометрической точки зрения, производная угла наклона касательной, проведенной к графику функции в точке М0(х0, f(x0)) к оси х.

Можно показать, что функция является дифференцируемой тогда и только тогда, когда ее приращение представимо в виде:

, - бесконечная малая при .

Если функция дифференцируема в точке х0, то она непрерывна в этой точке.

Правила вычисления производных :

1. 

Доказательство:

Если каждый из этих пределов существует и конечен: , то .

Теорема: если функции u(x) и v(x) являются дифференцируемыми в точке х, то функция u(x)+v(x) также является дифференцируемой в этой точке и справедливо равенство .

2. Для произведения аналогична теорема и доказательство.

.

Доказательство:

, учитывая, что , то получим, что

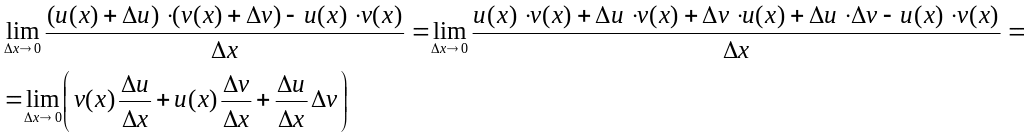
Предел каждого из слагаемых существует, v(x) и u(x) не зависят от , следовательно это константы, - производные, - бесконечно малая, следовательно .

Формулы:

Производная сложной функции: Если функция х=х(t) дифференцируема в точке t0, а функция дифференцируема в точке x0 = x(t0), то функция y(t)=f(x(t)) будет дифференцируема в точке t0 при этом .

Если функция дифференцируема в точке x0, то она распишется так: (*).

.

Утверждение: если функция дифференцируема в точке, то она в ней непрерывна.

x(t) дифференцируема в точке x0, следовательно x(t) непрерывна в точке x0, следовательно , следовательно .

Если (*) разделим на , то получим , так как бесконечно малая.

.

Формула Тейлора: пусть функция f(x) имеет производные до порядка (n+1) включительно в окрестности точки x0, тогда справедлива формула Тейлора:

.

R_n(x) – остаточный член в форме Лагранжа имеет вид: . Точка с лежит между х0 и х.

Остаточный член в форме Пеано: - бесконечно малое более высокого порядка малости чем (x – x₀)ⁿ

7. Дифференцирование функции многих переменных: производная по направлению, частные производные, дифференциал. Производная от сложных функций, градиент, направление убывания, геометрический смысл градиента.

Пусть функция z=z(x,y) определена в некоторой окрестности точки (x₀,y₀): U(x₀,y₀) Точка (x₀+Δx, y₀) ЄU(x₀, y₀).

Рассмотрим:

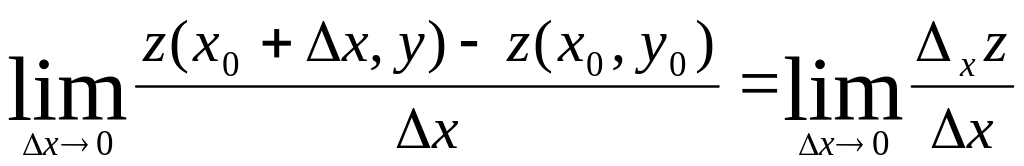
Если этот предел существует и конечен, то функция называется дифференцируемой по х в точке (x₀, y₀), а значение предела называют частной производной функции z по переменной х в точке (x₀, y₀):

Из определения производной видно, что остальные аргументы не меняются, т.е. являются константами, при вычислении производной по х.

Функция z(x,y) называется дифференцируемой по совокупности аргументов или просто дифференцируемой в точке (x₀,y₀), если ее полное приращение в точке (x₀,y₀) представлена в виде:

где является бесконечно малой более высокого порядка малости, чем

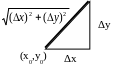при

(x₀+Δx,y₀+Δy)

Бесконечно малая более высокого порядка малости, т.е

Покажем, что ,а

Пусть Δy=0 => при

Разделим на Δx и перейдем к пределу.

Если функция z(x,y) дифференцируема по совокупности аргументов, то она дифференцируема по каждому из аргументов в отдельности, при этом ,

Обратное утверждение, вообще говоря, неверно.

Теорема (достаточное условие дифференцируемости функции): Если функция z=z(x,y) имеет частные производные , в некоторой окрестности U(x₀,y₀) точки (x₀,y₀) и эти частные производные непрерывны в самой точке (x₀,y₀), то функция z дифференцируема в точке (x₀,y₀) по совокупности аргументов.

Главная линейная часть полного приращения функции называется ее дифференциалом.

(если x, y –независимые переменные)

Если функция z(x,y) дифференцируема по совокупности аргументов в точке (x₀,y₀), то она непрерывна в этой точке по совокупности аргументов. Обратное утверждение, вообще говоря, неверно.

Геометрический смысл дифференцируемости:

С геометрической точки зрения, дифференцируемость функции z(x,y) по совокупности аргументов в точке (x₀,y₀) означает существование невертикальной касательной плоскости к поверхности z(x,y) в точке М(x₀,y₀, z((x₀,y₀)).

Производная сложной функции

Пусть функции дифференцируемы в точке (u₀,v₀)

Функция z(x,y) дифференцируема в точке (x₀,y₀), где x₀=x(u₀,v₀), y₀=y(u₀,v₀)

Тогда функция z=z(x(u,v), y(u,v)) имеет частные производные , в точке (u₀,v₀) при этом

Если x и y функции одного аргумента

То функция z(x(t), y(t)) также является функциями одного аргумента и можно говорить о полной производной.

Пусть функция z(x,y) определена в некоторой окрестности точки (x₀,y₀) и имеет частные производные

и

Пусть через точку (x₀,y₀) проходит ось образующая угол с осью X, и угол с осью Y. Тогда производной по направлению будет

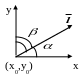
Производная по направлению равна скорости изменения функции в точке (x₀,y₀) в направлении вектора .

Если эта производная > 0, то функция z в точке (x₀,y₀) возрастает в данном направлении, иначе убывает.

Очевидно, что можно рассматривать как скалярное произведение двух векторов:

Градиент – это есть вектор

Вектор с координатами орт ( , ).

- направляющие косинусы вектора.

принимает наибольшее значение, когда ,т.е. когда , следовательно, градиент направлен в сторону наибольшего роста функции в данной точке, при этом