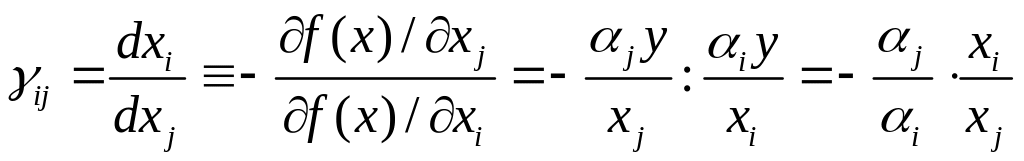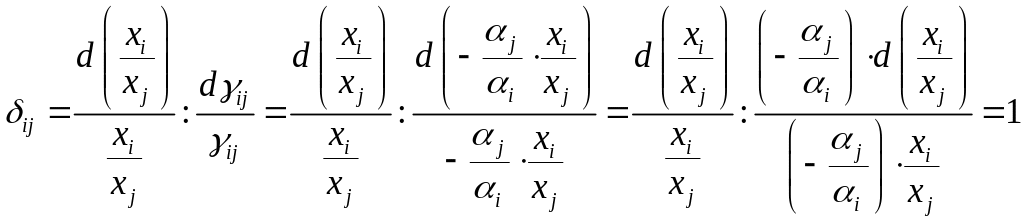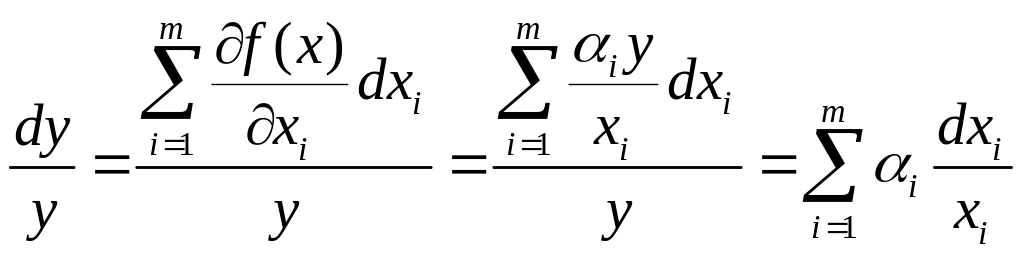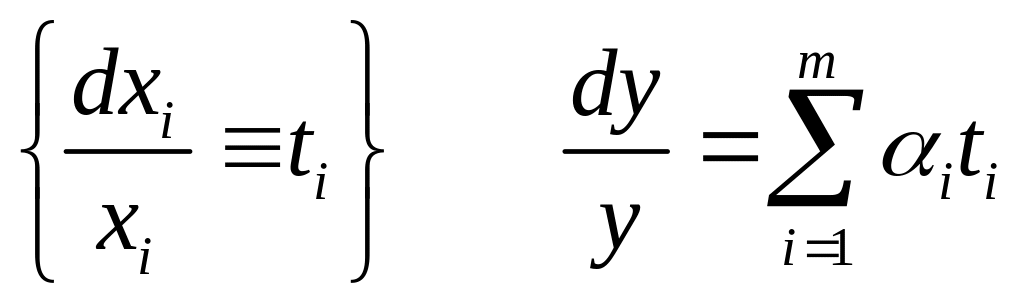- •3. Системы линейных алгебраических уравнений. Условие сущ-ния решения, решение систем по формулам Крамера и методом исключений, фундаментальная система реш-й.
- •5. Пределы и непрерывность. Числовая последовательность и ее предел. Определение функции, ее непрерывность на языке "эпсилон-дельта" и языке пределов, равномерная непрерывность.
- •6, Производная функция одной переменной. Определение, геометрический смысл, простейшее правило вычисления производной. Производная сложной функции. Формула Тейлора.
- •8. Определенный интеграл и его геометрический смысл (задача о площади криволинейной трапеции). Приближенное вычисление определенных интегралов, формулы трапеций и Симпсона.
- •12. Закон больших чисел и центральная предельная теорема.
- •13. Регрессионный анализ: линейная и нелинейная регрессия, статистические свойства оценок коэффициентов регрессии.
- •14. Проверка гипотез. Критерий χ2. Ошибки 1-го и 2-го рода. Лемма Неймана-Пирсона.
- •15. Метод максимального правдоподобия. Точечное и доверительное оценивание параметров гауссовского распределения.
- •Вопрос 16: Тренд, сезонная и циклическая компоненты временного ряда.
- •17.Модели тренда (свойства логистической и линейной кривой).
- •18. Методы выделения сезонной компоненты временного ряда (метод скользящих средних).
- •19. Приведение задач линейного программирования к каноническому виду. Методы искусственного базиса.
- •I метод искусственного базиса
- •II метод искусственного базиса
- •20. Симплексный метод (см), основные принципы, алгоритм.
- •21. Двойственный симплекс-метод, основные принципы, алгоритм. Случаи, когда удобно применять двойственный симплексный метод. (дсм)
- •22. Задача максимизации прибыли при заданных ценах на продукцию и ресурсы. Анализ оптимальных решений с помощью множителей Лагранжа.
- •23. Транспортная задача замкнутого типа: постановка, существование решения, метод потенциалов.
- •24. Транспортная задача незамкнутого типа. Постановка, способ сведения к задаче замкнутого типа(с обоснованием). Алгоритм решения.
- •25. Теорема о необходимых и достаточных условиях оптимальности смешанных стратегий. Метод сведения решения игр к решению задачи линейного программирования.
- •26. Функция выигрыша в матричных играх без седловой точки. Смешанные и оптимальные смешанные стратегии. Метод сведения решения матричных игр к задаче линейного программирования.
- •27. Методы наискорейшего и координатного спуска для минимизации выпуклой функции без ограничений. Их алгоритмы и геометрическая интерпретация
- •28. Типичные производственные функции с несколькими ресурсами: линейная пф, степенная пф, пф с постоянными пропорциями. Коэффициенты эффективности использования ресурсов для этих типов функций
- •1. Линейная производственная функция:
- •2. Степенная производственная функция:
- •3. Производственная функция с постоянными пропорциями:
- •33. Модель с фиксированным размером заказа
- •34. Модель с фиксированным уровнем запасов
- •35. Двухуровневая система управления товарными запасами, (s,s)-система.
- •36. Математическая модель и схема статического моб в денежном выражении. Методологические вопросы построения моб.
- •Методологические вопросы построения моб Классификация отраслей
- •Метод учета продукции
- •Способ оценивания продукции
- •Общие предпосылки модели моб
- •Дополнение ограничений моб по производственным ресурсам
- •37. Свойства коэффициентов прямых материальных затрат в моб. Определение косвенных и полных материальных затрат.
- •38. Основные понятия теории баз данных: объект, свойство, связь. Диаграмма «сущность-связей». Логическая, физическая, концептуальная схемы базы данных
- •39. Реляционная модель данных. Основные понятия: отношение, кортеж, домен. Получение нормальных форм отношений из диаграммы «сущность-связь». Реляционная алгебра и ее основные понятия.
- •Первая нормальная форма
- •Вторая нормальная форма
- •Третья нормальная форма
- •Нормальная форма Бойса-Кодда
- •Четвертая нормальная форма
- •Пятая нормальная форма
- •40. Реляционная алгебра, основные операторы реляционной алгебры. Связь языка sql с операторами реляционной алгебры.
- •41. Реляционная модель данных. Теория нормализации. Нормальные формы: первая, вторая, третья, Бойса-Кодда.
- •42. Физическая организация баз данных. Файлы: последовательные, с прямым доступом, с хеш-адресацией, индексно-последовательные, в-деревья.
- •43. Назначение и основные компоненты операционных систем. Управление памятью. Управление внешними устройствами. Защита данных. Интерфейс прикладного программирования. Пользовательский интерфейс.
- •Пользовательский интерфейс
- •47. Функция организационного управления: сбор и первичная обработка данных, моделирование ситуации выбора, прогнозирование неуправляемых параметров
- •Сбор и первичная обработка данных
- •Моделирование ситуации выбора
- •Идентификация модели ситуации выбора (прогнозирование неуправляемых параметров)
- •48. Функция организационного управления: планирование, принятие решения организация исполнения решения, контроль, координация.
- •Планирование (вычисление управляемых параметров)
- •Принятие решений
- •Организация исполнения решений
- •Контроль
- •Координация
- •Вопрос 11. 20
- •Вопрос 16: Тренд, сезонная и циклическая компоненты временного ряда. 31
28. Типичные производственные функции с несколькими ресурсами: линейная пф, степенная пф, пф с постоянными пропорциями. Коэффициенты эффективности использования ресурсов для этих типов функций
Производственная функция (ПФ) выражает зависимость результата производства от затрат ресурсов. При описании экономики (точнее, ее производственной подсистемы) с помощью ПФ эта подсистема рассматривается как «черный ящик», на вход которого поступают ресурсы X1,…, Xп, а на выходе получается результат в виде годовых объемов производства различных видов продукции Y1,…Ym. Y=f(X);
ПФ применяются для анализа влияния различных сочетаний факторов на объем выпуска в определенный момент времени (статический вариант П. ф.) и для анализа, а также прогнозирования соотношения объемов факторов и объема выпуска в разные моменты времени (динамический вариант Пф.) на различных уровнях экономики - от фирмы (предприятия) до народного хозяйства в целом (агрегированная ПФ, в которой выпуском служит показатель совокупного общественного продукта или национального дохода и т. п.).
С точки зрения ресурсов различают ПФ с взаимозаменяемыми и взаимодополняемыми ресурсами. Взаимозаменяемость предполагает, что один и тот же объем выпуска продукции может быть получен при разных комбинациях объемов ресурсов.
Изокванты – линии уровня производственной функции, множество тех точек для которых выпуск постоянен при разных затратах ресурсов.
Изоклинали- линии наибольшего роста ПФ, они ортогональны изоквантам.
Показатели:
Средняя эффективность
 – показывает отдачу от каждой единицы
i-го ресурса;
– показывает отдачу от каждой единицы
i-го ресурса;Предельная эффективность
 – показывает предельный прирост выпуска
продукции при увеличении затрат i-го
ресурса на малую величину.
– показывает предельный прирост выпуска
продукции при увеличении затрат i-го
ресурса на малую величину.
 – только для взаимозаменяемых ресурсов;
– только для взаимозаменяемых ресурсов;Эластичность выпуска
 – отражает отношение относительного
прироста продукции к относительному
приросту i-го ресурса;
– отражает отношение относительного
прироста продукции к относительному
приросту i-го ресурса;
|
|
|
– показывает, на сколько % должно измениться отношение объемных затрат ресурсов i и j, чтобы при этом норма замещения изменилась на 1%.
|
1. Линейная производственная функция:
![]()
![]()
![]()
|
|
|
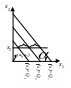
Предельная эффективность постоянна, т.е. от каждой новой ед. ресурса выпуск возрастает на ед. Ресурсы полностью взаимозаменяемые с постоянной нормой замены. Изобразим на графике поведение функции. На
уровне x2
прирост x1
будет давать один и тот же прирост
производства, т.е.
|
2. Степенная производственная функция:
![]()
![]()
![]()
При фиксированном выпуске продукции предельная эффективность i-го ресурса падает с ростом затрат на него.
Предельная норма замещения растет с ростом удельных затрат j-го ресурса, т.е. для компенсации одной единицы продукции i-го ресурса требуется все большее количество затрат j-го ресурса.
При изменении коэффициента эластичности замещения на 1% соотношение продуктов также должно измениться на 1%. Коэффициент эластичности замещения равен 1, что является недостатком модели, так как согласно статистическим исследованиям такого быть не должно. Рассмотрим, каким образом темп роста производства зависит от темпов роста затрат ресурсов:
Темп роста объемов производства линейно зависит от темпов роста затрат ресурсов:
Если
объем затрат ресурсов изменился на
1% для каждого ресурса, то объем выпуска
продукции изменится на
Во многих случаях
для
|
Степенная функция является разновидностью функции Кобба-Дугласа:
L – затраты труда,
– затраты труда,
K
– затраты капитала, тогда
![]()
где

Функция предложена в 1920 году.
Изокванты степенной функции имеют асимптоты в виде осей координат, они не пересекаются для разных объемов производства.
Недостаток модели: 1) в каком бы очень маленьком количестве мы не имели ресурс, его всегда можно заменить достаточно большим количеством других ресурсов. 2) также равенство эластичности взаимозаменяемости 1. Поэтому ведутся разработки по избавлению от этого недостатка. Например, создаются функции с постоянной эластичностью замены, не равной 1.

 – показывает, какое количество i-го
ресурса может быть высвобождено из
производства при увеличении затрат
j-го ресурса на 1,
при неизменном выпуске;
– показывает, какое количество i-го
ресурса может быть высвобождено из
производства при увеличении затрат
j-го ресурса на 1,
при неизменном выпуске;