21. Двойственный симплекс-метод, основные принципы, алгоритм. Случаи, когда удобно применять двойственный симплексный метод. (дсм)

Предположим, что имеется з-ча:

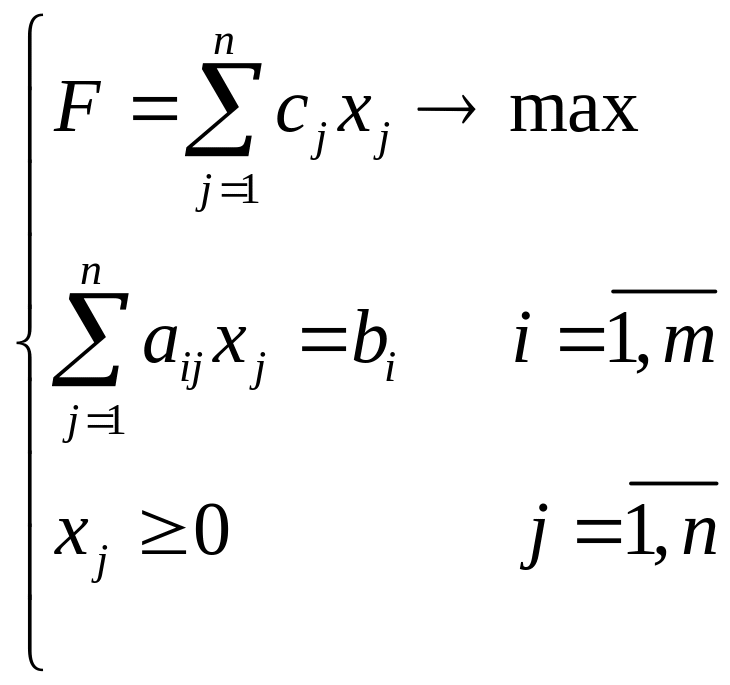
Исходным пунктом является выбор такого базиса (таких базисных переменных): (1),

что выполняется:

(2)

Надо знать: Принципиальная разница от обычного симплексного метода: искусственные перем-ые вводить не надо и вектор Х₀, соот-щий базису A_Б, вообще говоря м.б. недопустимым, т.е. среди его компонент м.б. отриц-ые (чего не м.б. в обычн. симпл.мет., т.к. там всегда вектор есть угловая точка). Нач-ая точка м. лежать вне обл-ти допустимых реш-ий.

В двойственном симпл.мет. мы треб-м, чтобы все ∆_j были не отриц-ми.

Основной принцип ДСМ закл-ся в том, что при переходе от одного базиса к другому выполнялось (2) и целевая ф-ия убывала.

Алгоритм ДСМ:

1. Выбираем базис (1) такой, что вып-ся (2) и строится симплексная таблица

2. если все b_i≥0, то з-ча решена. Если нет, то переходим к шагу 3.

3. Нах-т все строчки с b_i<0; если для нек-го i с b_i<0 остальные эл-ты ≥ 0, то з-ча несовместная.

4. В противном случае выбирается i₀ при к-ой b_i<0. Нах-ся: 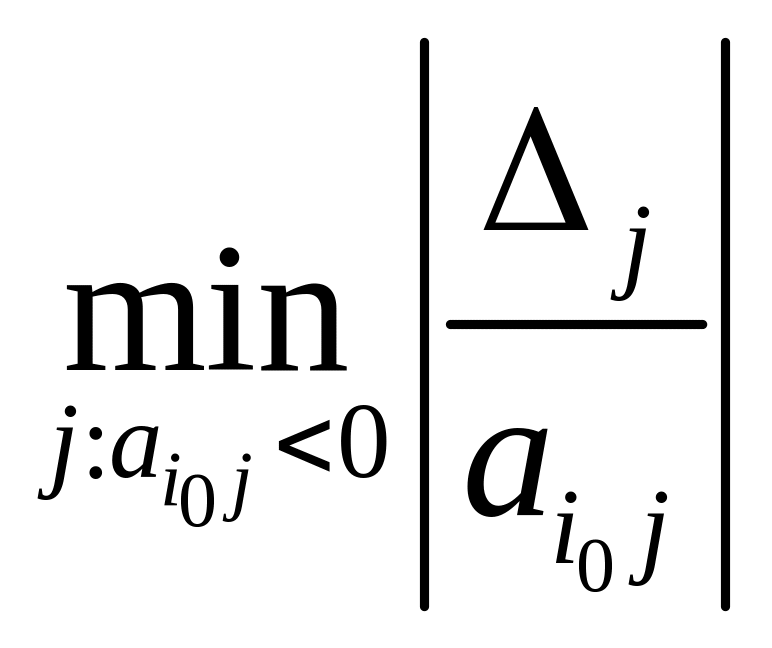. Там, где минимум достигается, будет разрешимый столбец j₀, разрешающий эл-т .

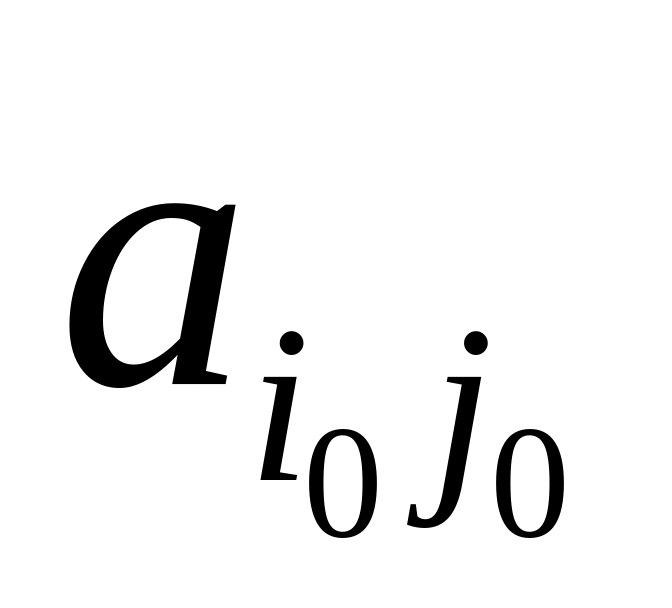5. Строится новая симплексная таблица и переходим к шагу 2.

Случаи удобности применения ДСМ

Применимость ДСМ огр-но сложностью выбора исх-го базиса A_Б. Рассмотрим 2 типа задач.

1тип:

Вводим доп-ые перем-ые и получаем:

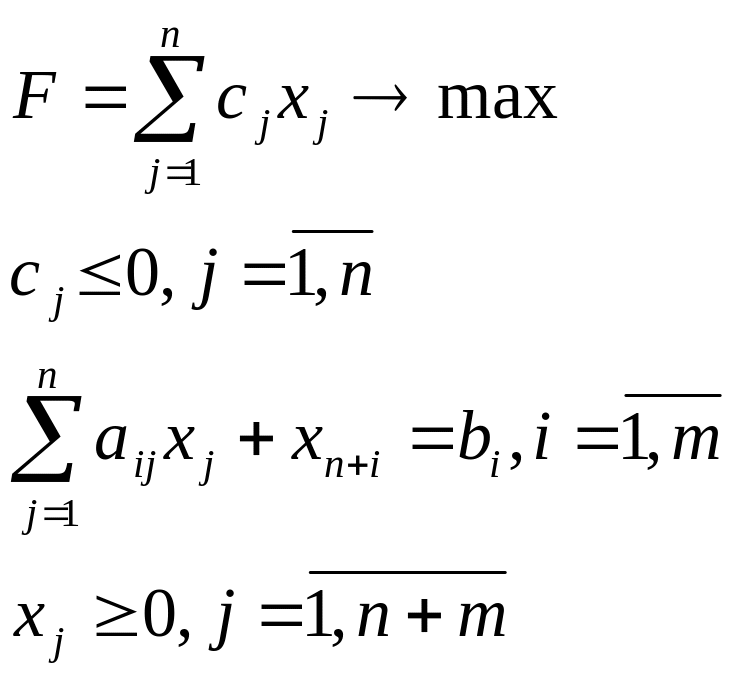
В кач-ве базисных перем-ых выбираем доп-ые. Доп-ые перем-ые в ф-ию F входят с нулевыми коэф-ами. След-но, С_Б=0. След-но:

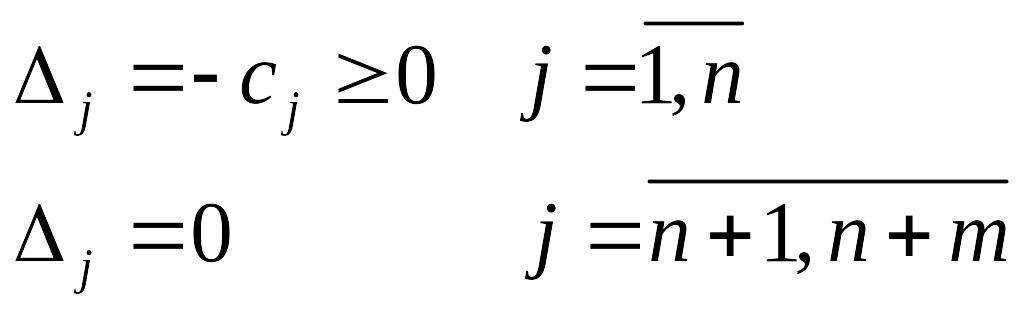
Таким образом, задача подготовлена к применению ДСМ.

2 тип:

В некоторых практических задачах после реш-ия можно обнаружить, что найденное решение не отражает действительную ситуацию. Чаще всего это происходит по причине того, что забыли вкл-ть нек-ые огр-ия. Т.е. его надо вкл-ть и з-ча д.б. решена заново. Однако, если вышеуказ-ое огр-ие имеет вид нер-ва, то лучше всего применять ДСМ.

Предположим, что з-ча была решена и получено оптим-ое реш-ие, где первые m компонент базисные, все ∆_j≥0. Добавляем такое нер-во:

Вводим дополнительную переменную, чтобы получилось рав-во:

Очевидно, что эта новая перем-ая входит в целевую ф-ию с коэф-ом 0. Составим расширенную м-цу коэф-ов в огр-иях.

Б.П. С.П. x_n+1

Вычтем из последней строки первую, умноженную на а_m+1,1. Затем из последней строки – вторую, умноженную на а_m+1,2. … Из последней – предпоследнюю, умноженную на а_m+1,n. (Если записать это ф-лой: ).

В рез-те получим м-цу:

Б.П. С.П. x_n+1

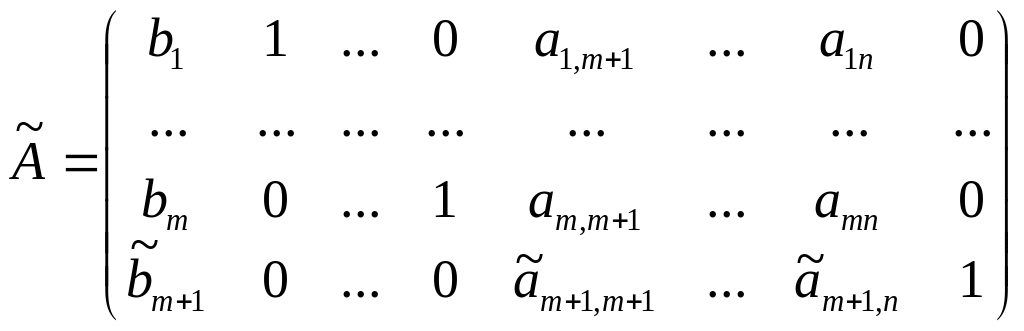
Вектор x_n+1 присоединяем к базисным, т.о. Ã есть симплексная таблица. Надо записать еще С₀=0, C₁, …, С_n, C_n+1=0, оценки ∆_j, к-ые будут совпадать с заключительной симпл.таблицей, т.е. все ∆_j≥0. Если при этом ≥0, то з-ча решена.

22. Задача максимизации прибыли при заданных ценах на продукцию и ресурсы. Анализ оптимальных решений с помощью множителей Лагранжа.

Пусть производится один продукт ценой P₀, используются ресурсы с ценами . Требуется решить задачу максимизации прибыли при заданных P₀ и p:

max (P₀f(x) – <p, x>) (1)

x  0 (2)

Исследование задачи будем проводить с помощью функции Лагранжа:

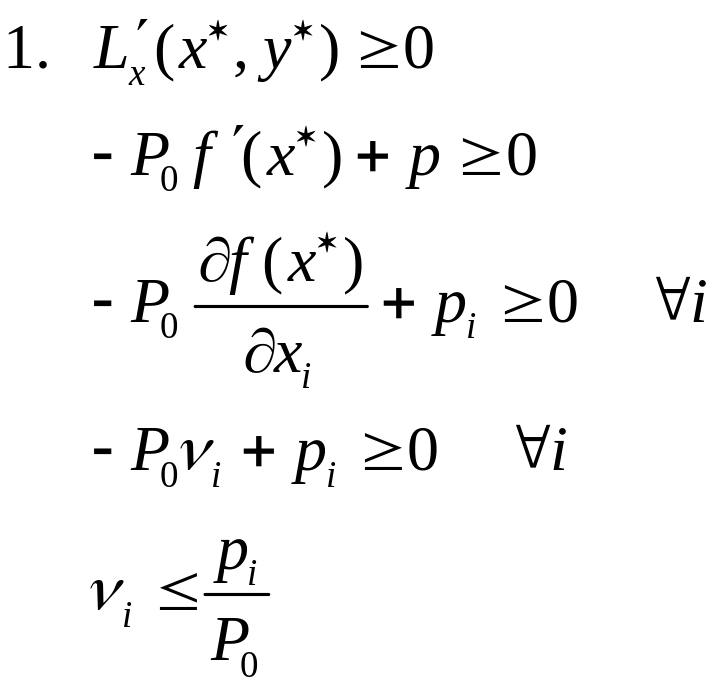
– балансовое соотношение

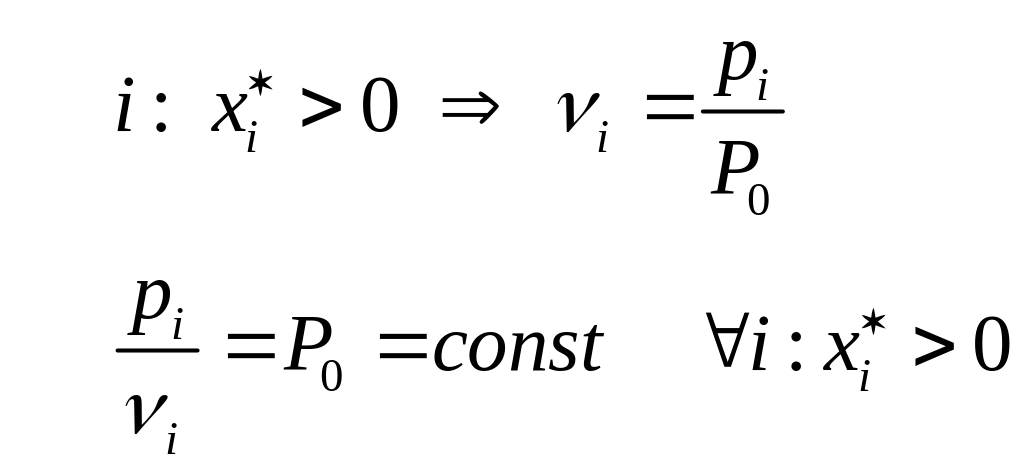
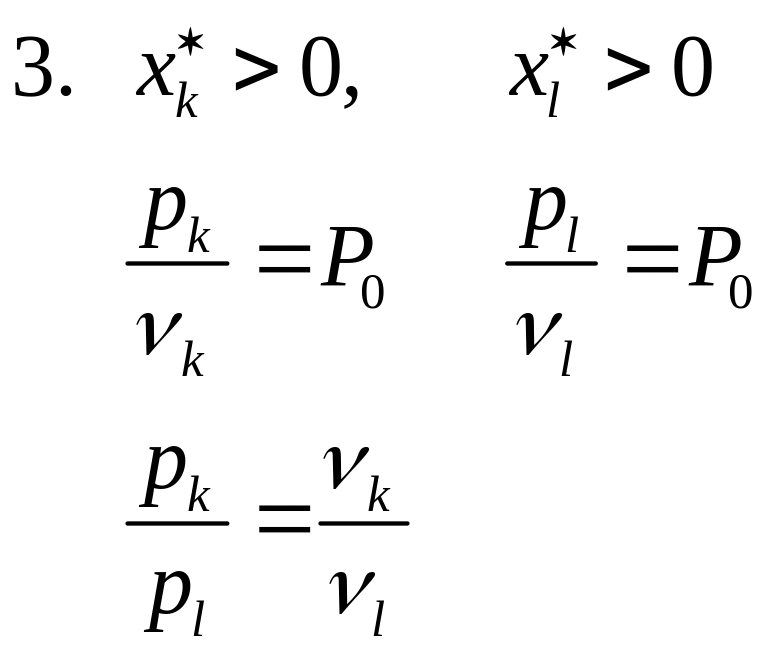
В оптимальном плане x^* для любых используемых ресурсов отношение цены к предельной эффективности постоянно. Для этих же ресурсов показали, что соотношение предельных эффективностей равно соотношению цен. Наибольшая отдача будет от тех ресурсов, которые имеют самую большую предельную эффективность в текущей точке.

Эти свойства не имеют универсального значения. Они применимы только тогда, когда эффективность ресурса при увеличении масштаба производства сокращается. При этой ситуации нахождение оптимального плана задачи (1)-(2) можно интерпретировать как процесс выравнивания соотношения цен и предельных эффективностей.

Предельная эффективность – показывает предельный прирост выпуска продукции при увеличении затрат i-го ресурса на малую величину.