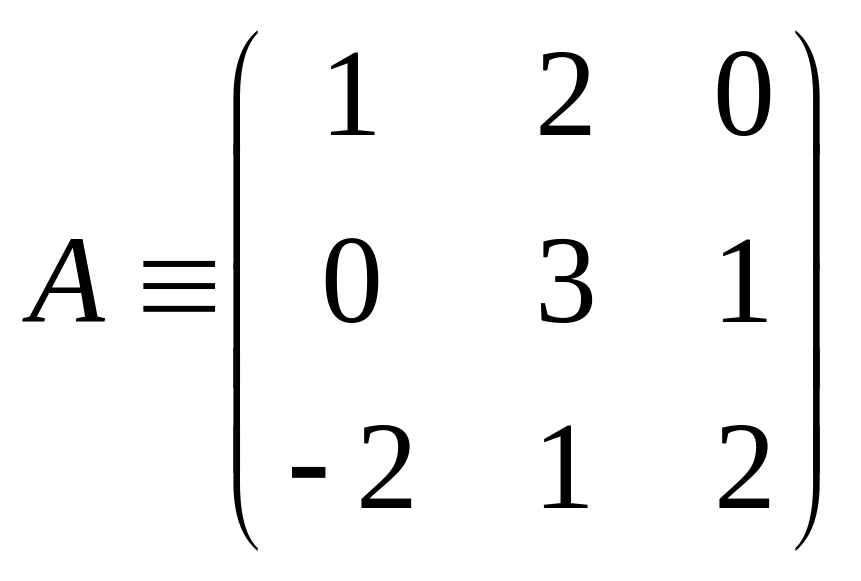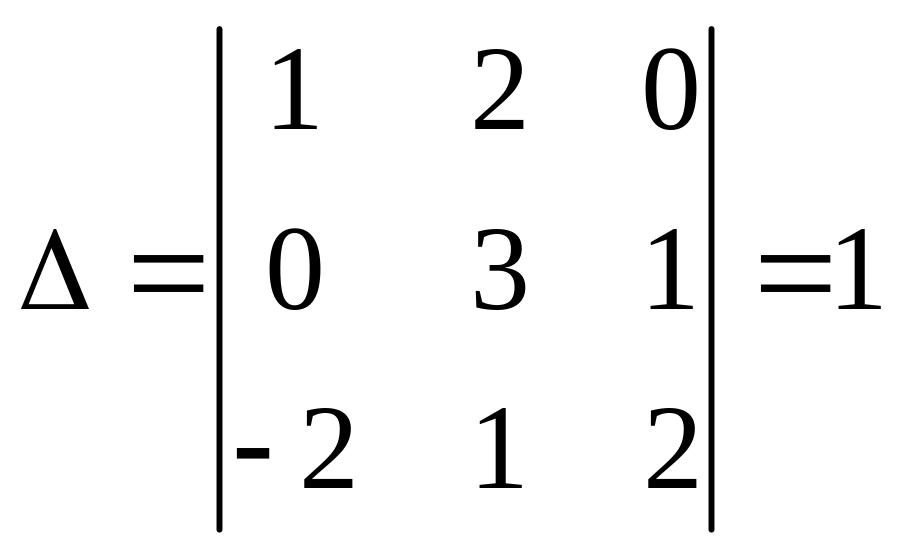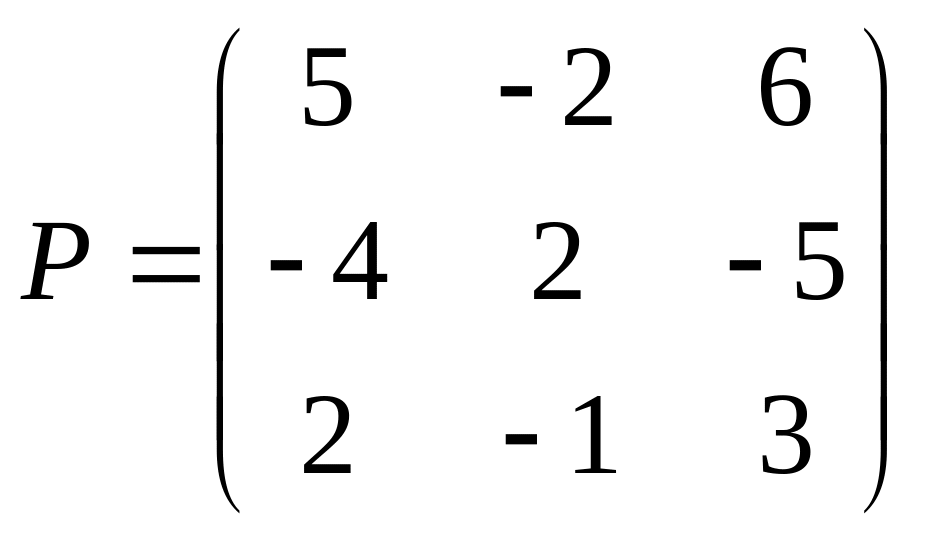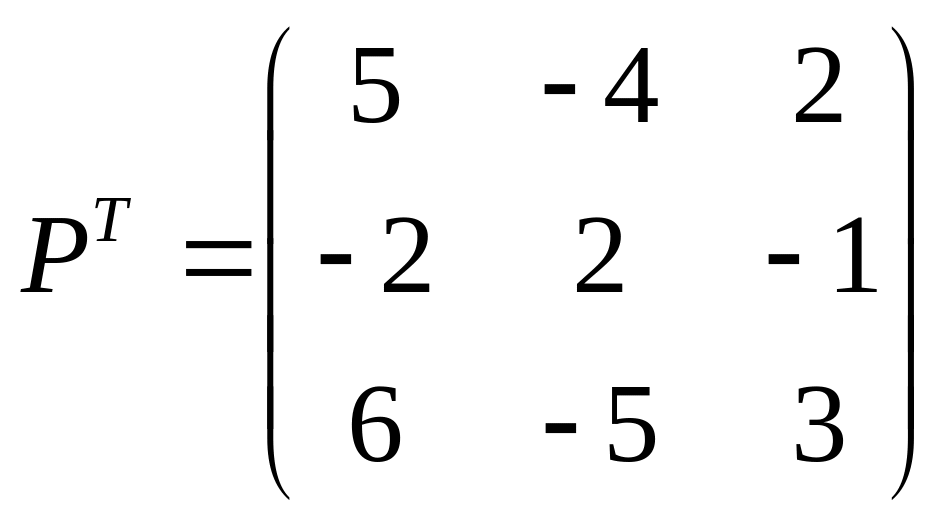12

1. Матрицы. Определение, умножение матриц на число и сложение их, умножение матриц, ранг матрицы и его нахождение путем элементарных преобразований, вычисление обратной матрицы по формулам и методом исключения.

Матрицы – это прямоугольные таблицы элементов (чисел, функций) из m строк и n строк.

m, n – порядки матрицы, они определяют размерность матрицы

Обозначение:

Если m = n, то матрица называется квадратной. В случае квадратной матрицы вводятся понятия главной и побочной диагонали матрицы (главная: i = j; побочная: i = n - j + 1).

[Равенство двух матриц] A = B, если

1) dim A = dim B

2)

Основные операции над матрицами:

1. Пусть dim A = dim B (необходимое условие), тогда суммой матриц А и В называется новая матрица С_mn: с_ij=a_ij+b_ij 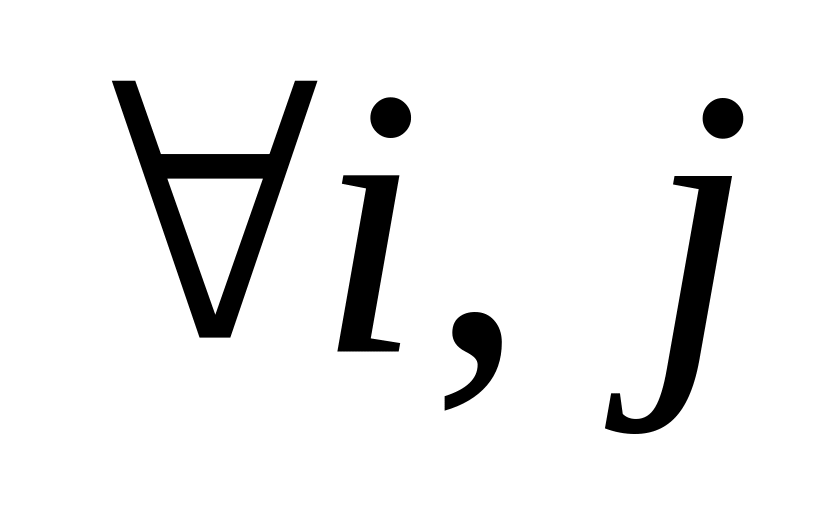. (1)

Обозначение: Операция получения суммы называется сложением.

Свойства операции сложения:

1 А+В=В+А (коммутативность)

2 (А+В)+С = А+(В+С) (ассоциативность)

Док-во: из определения.

2. Произведением матрицы А на число 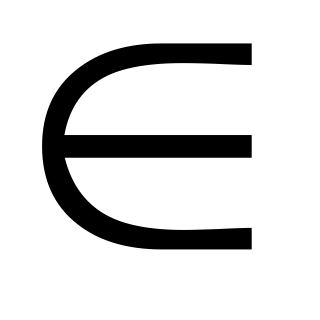 R называется матрица С: c_ij = a_ij (2)

Обозначение: (по определению, доказывать не надо)

Свойства:

1 ()А = (А) (ассоциативность)

2 (А+В) = А+В (дистрибутивность операции умножения относительно сложения матриц)

3 (+)А = А+А (дистрибутивность операции умножения относительно сложения чисел)

Док-во из определения, расписываются левые и правые части и сравниваются.

3. Умножение матрицы на матрицу (перемножение матриц)

Произведением м-ы А_mn на м-цу В_np называется матрица С_mp: (3)

Обозначение:

(Строка i матрицы А умножается на столбец j матрицы В в смысле скалярного произведения)

Свойства:

1 (АВ)С=А(ВС) (ассоциативность)

2 А(В+С) = АВ+АС

(А+В)С = АС+ВС (дистрибутивность)

Док-во через сравнение размерностей прав и лев частей.

ЗАМ: Произведения АВ и ВА определены и имеют одну и туже размерность лишь тогда, когда, А и В – квадратные матрицы одного и того же порядка. Для таких матриц можно исследовать коммутативность. Вообще говоря, коммутативность не выполняется АВ ВА. Можно показать на простых примерах. Имеются некоторые частные случаи, когда коммутативность выполняется:

Если D = D_n – диагональная матрица, то . В частности если D = E и D = 0.

Минором k-ого (M_k) (где k≤{m,n}) порядка м-цы А_{m n} наз-ся определитель k-ого порядка с элементами, расположенными на пересечении произвольных k строк и k столбцов. Ес.

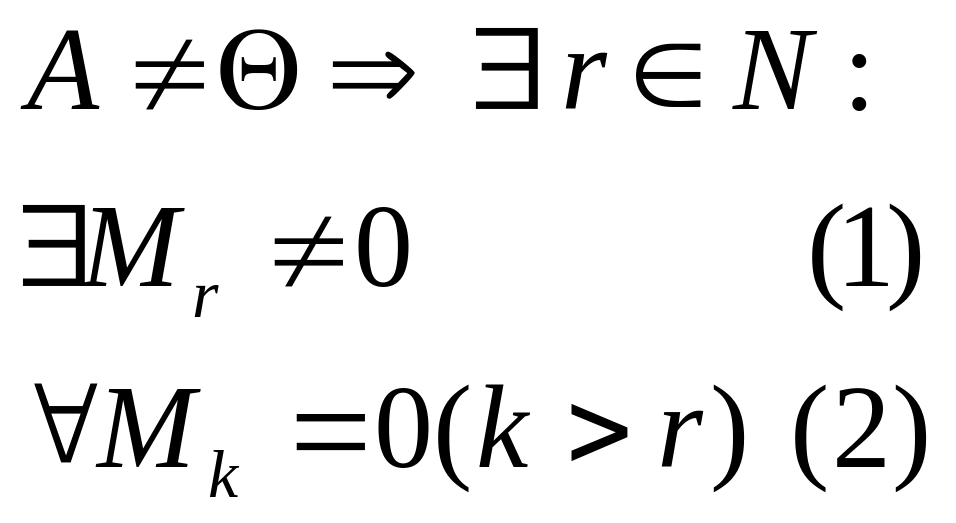
Число r, обладающий св-вами 1 и 2 наз-ют рангом м-цы А. При этом Mr наз-ют базисным минором, строки и столбцы, образующие минор сами наз-ся базисными.

Ранг матрицы – max порядок отличных от 0 миноров r(A)=rang(A).

Из Т. о базисном миноре (базисные строки (столбцы) линейно независимы; любая строка (столбец) представляется в вилле линейной комбинации базисных строк) следует, что ранг матрицы есть max число линейно независимых строк или столбцов.

Находят ранг несколькими способами:

1. методом элементарных преобразований. Используют тот факт, что элементарные преобразования матрицы не меняют ее ранг. Элементарные преобразования:

• перестановка любых двух строк (столбцов)

• умножение любой строки (столбца) на любое число, не равного 0

• умножение любой строки (столбца) на любое число и прибавление полученного результата к любой строке (столбцу)

Используя элементарные преобразования, приводят матрицу к треугольному виду, более того можно привести к диагональному виду.

Пр-р:

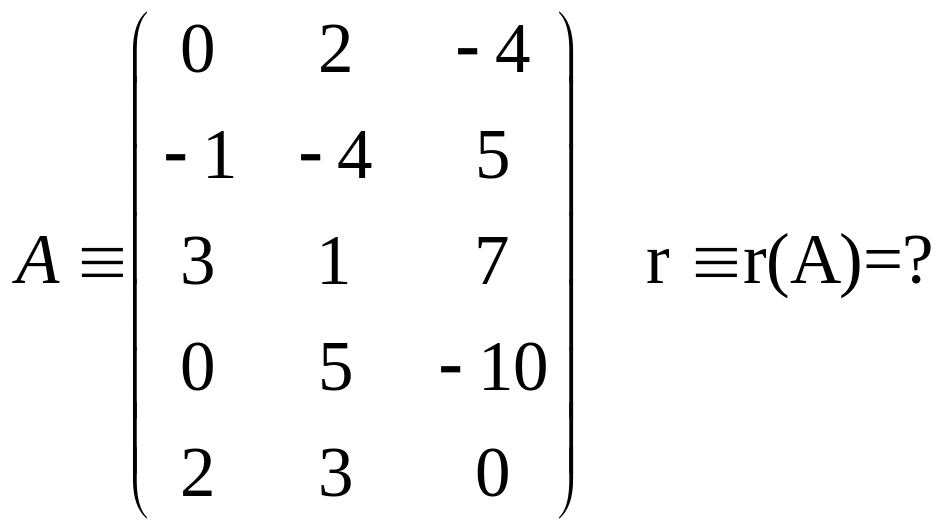
по построению первого определителя, отличного от нуля, ранг м-цы=2.

2. метод окаймляющих миноров. Пусть в матрице найден , тогда рассматривают лишь те миноры (k + 1) порядка, которые содержат в себе .

Если все такие миноры = 0, то r(A) = k. Если же среди них , то процесс повторяется.

Обратная матрица.

Дана м-ца

Зам: м-ца А^-1 наз-ся обратной к А, если АА^-1=А^-1А Е, где Е – единичная м-ца.

А^-1 существует тогда и только тогда, когда

Нахождение обратной матрицы

1. По формулам:

1. Вычисляется ,

2. Если det A 0, то вычисляется P=P_A (А_ij)_{n n} (где 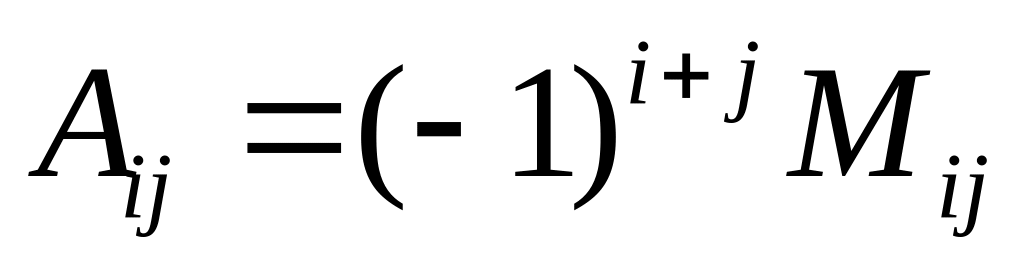– алгебраическое дополнение),

3. транспонируем В=Р^Т,

4. .

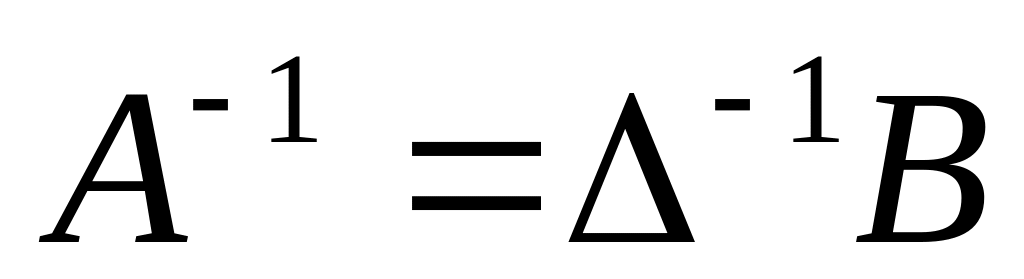Пример

1. 

2. 

3. 

4. 

2. Метод исключения (на основе метода Гаусса)

Образуем систему линейных уравнений , (1)

АХ=У. (2)

X – неизвестные

Y – условно считаются известными.

По теореме Крамера система имеет единственное решение (так как )

Для построения обратной матрицы систему (2) решаем методом Гаусса, т.е. методом последовательного исключения:

,

Х=ВУ,

С другой стороны, с учетом (2) Х= А^-1У. Так как решение единственно, то В= А^-1.

Пример

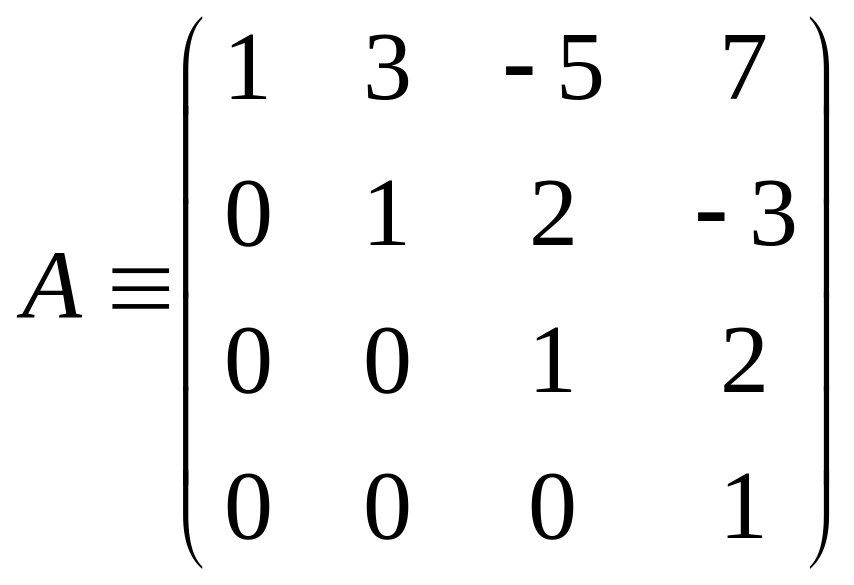
Составляем СЛАУ

х₄=у₄; x₃=y₃-2y₄; x₂=y₂-2(y₃-2y₄)+3y₄=y₂-2y₃+7y₄; x₁=y₁-3y₂+11y₃-38y₄.

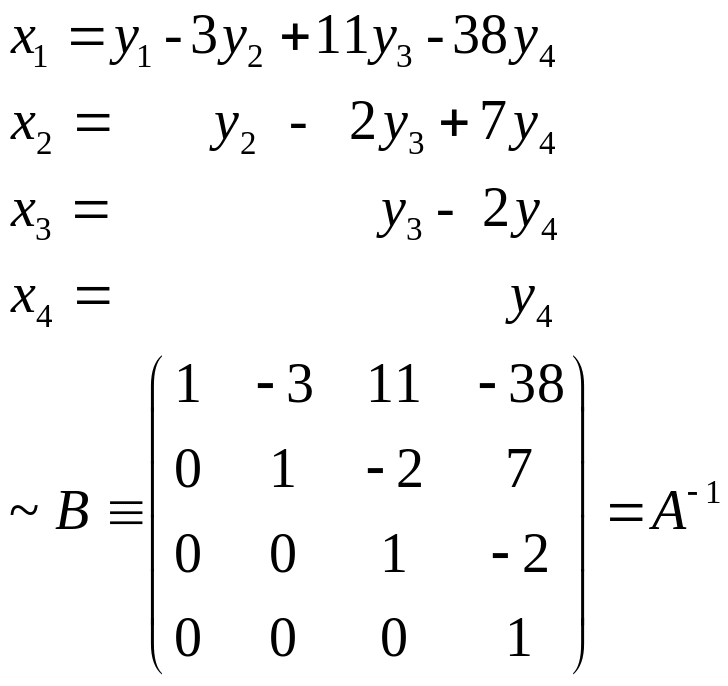
2. Определители. Определение и основные свойства (транспонирование, изменение порядка строк или столбцов, умножение на число, сложение строк или столбцов, разложение определителя по элементам строки или столбца). Вычисление определителей 2-го и 3-го порядков.

Каждой матрице А(a_ij)_nn по ниже следующему правилу ставиться число – который называется определитель соответствующей матрицы А.

Понятие определителя произвольного порядка можно ввести по индукции:

1) Если n=1 => а₁₁.

2) Если n=2 =>  а₁₁а₂₂ – а₂₁а₁₂₌ .

3) если таким образом уже введен определитель n-1 порядка, то определитель nго порядка называется



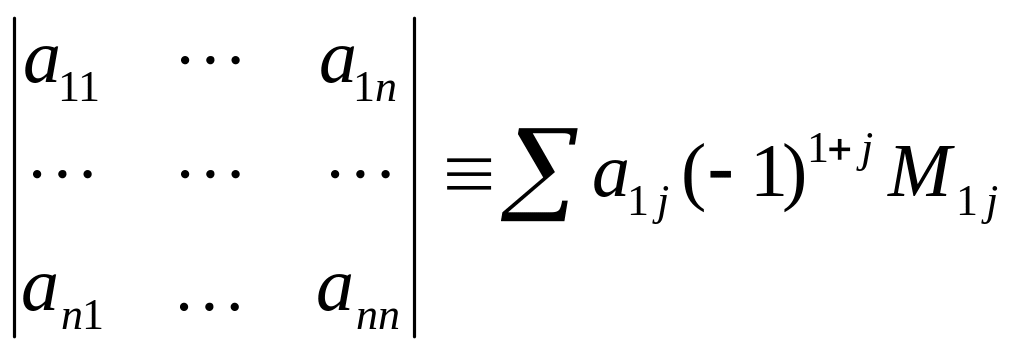
M_1j – det (n-1)-ого порядка (j=1,n).

!!!Отличие определителя от матрицы!!!

– умножается вся строка

– умножается одна строка или столбец

Свойства det:

1 При замене строк столбцами, т.е. при транспонировании величина определителя не меняется.

По правилу треугольника распишем и . Сравнивая результаты, получим, что

Это свойство устанавливает равноправность строк и столбцов => дальнейшие свойства достаточно сформулировать лишь для строк.

2 При перестановке любых 2-х строк определитель меняет лишь знак (доказательство на примере с правилом треугольника).

3 Если элементы 2-х строк равны, то det=0.

4 Общий множитель всех элементов некоторой строки можно вынести за знак det.

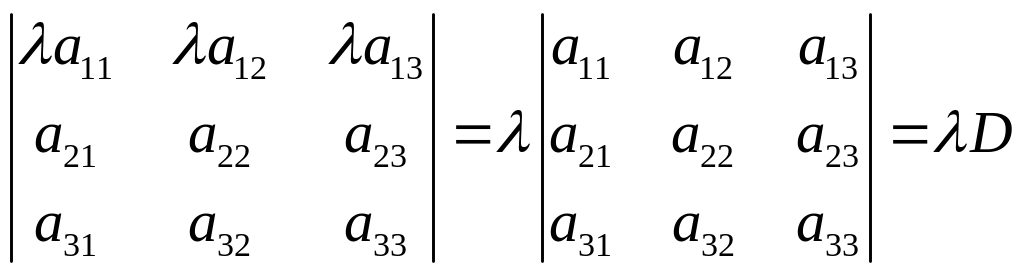
Доказательство – достаточно учесть, что в формуле треугольника каждое слагаемое содержит строго по одному элементу каждой строки и столбца. Следовательно, согласно правилу треугольника исходный определитель представляется в виде суммы шести слагаемых, причем каждое слагаемое обладает множителем , который выносится за скобки, а в скобках – выражение, равное D.

5 Если все элементы некоторой строки = 0, то det = 0.

Доказательство – достаточно в 4 взять =0.

6 Если соответствующие элементы 2-х строк пропорциональны, то det=0.

Доказательство – на основе 4 можно вынести коэффициент пропорциональности за знак определителя и по 3 det=0).

7 Если элементы некоторой строки представляют собой сумму 2-х слагаемых, то det может быть представлен в виде суммы 2-х det, у которых элементы рассматриваемой строки = соответствующим слагаемым.

Доказательство.

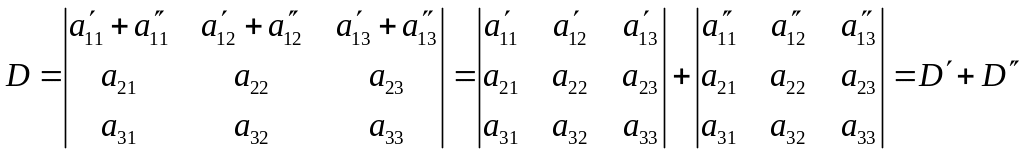
Рассуждения как в 4.

8 Если к элементам некоторой строки прибавить элементы другой строки, умноженные на любое число, то величина det не изменится.

Доказательство:

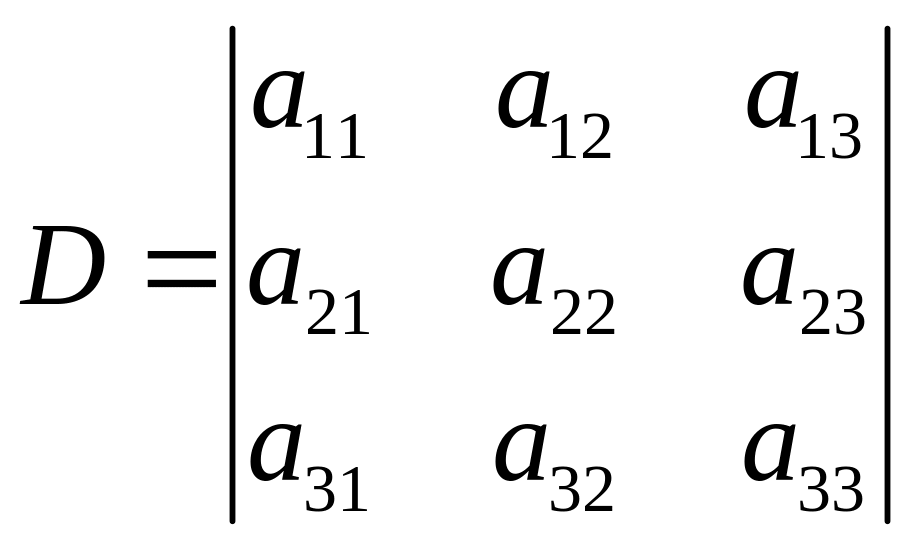
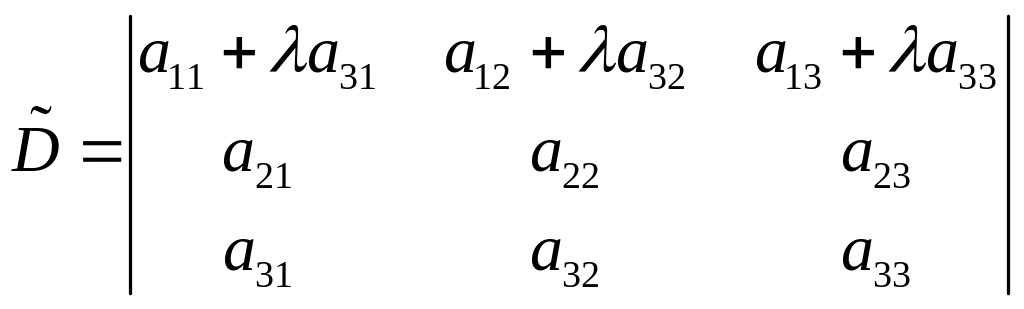
(св-во 6,7)

T[Разложение det по строке]

Разложение по строке

Пр:

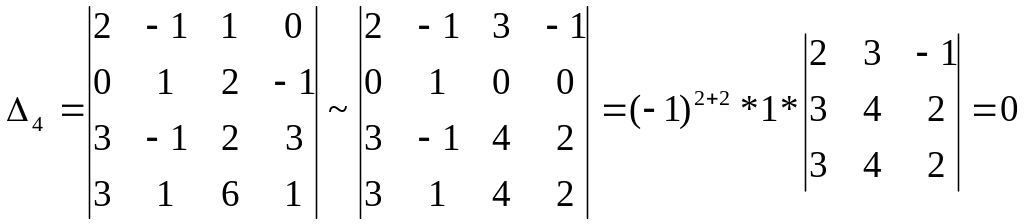
3. Системы линейных алгебраических уравнений. Условие сущ-ния решения, решение систем по формулам Крамера и методом исключений, фундаментальная система реш-й.

СЛАУ называется система n-го порядка: (1)

СЛАУ можно представить в виде матрицы АХ = В, где

– известные коэффициенты системы (1)

– известные правые части системы (1)

– неизвестные (искомые) величины

• Набор 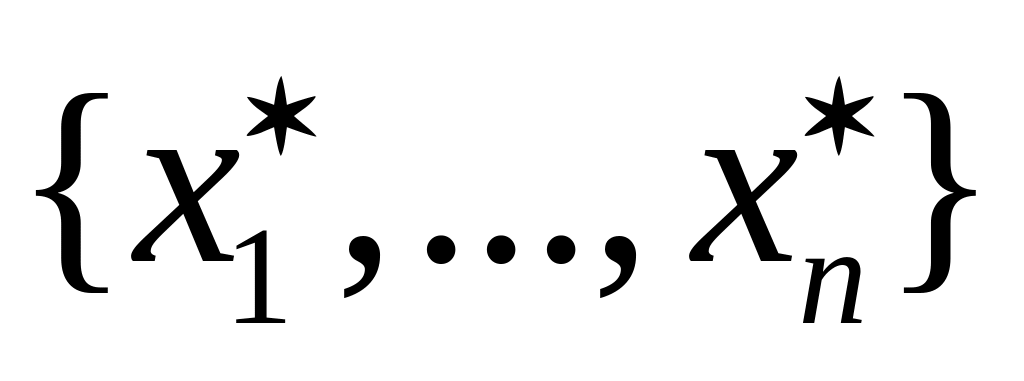(n-мерный набор) называется решением СЛАУ, если при подстановке их вместо соответствующих неизвестных 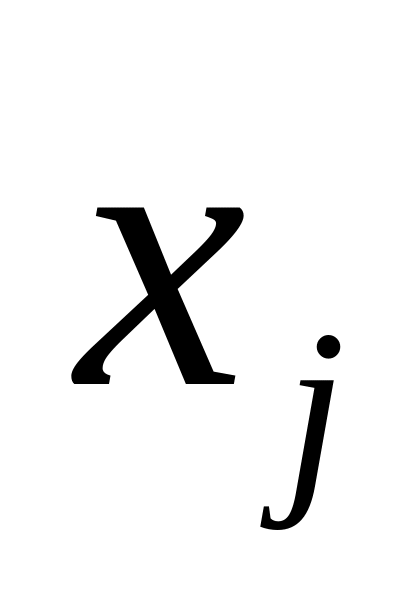каждое из уравнений системы превращается в истинное равенство (набор удовлетворяет (1)).

• Если система обладает хотя бы 1 решением, она называется совместной.

• Если имеется лишь единственное решение, то она называется определенной.

• Если имеется более 1 решения, то система называется неопределенной.

• Если нет ни одного решения, то она называется несовместной.

• Если решение одной системы является решением другой системы, то системы называются равносильными.

А – основная матрица, – расширенная матрица

Условия совместимости: Т. Кронекера-Капелли.

Система совместна (имеет хотя бы 1 реш-е) 

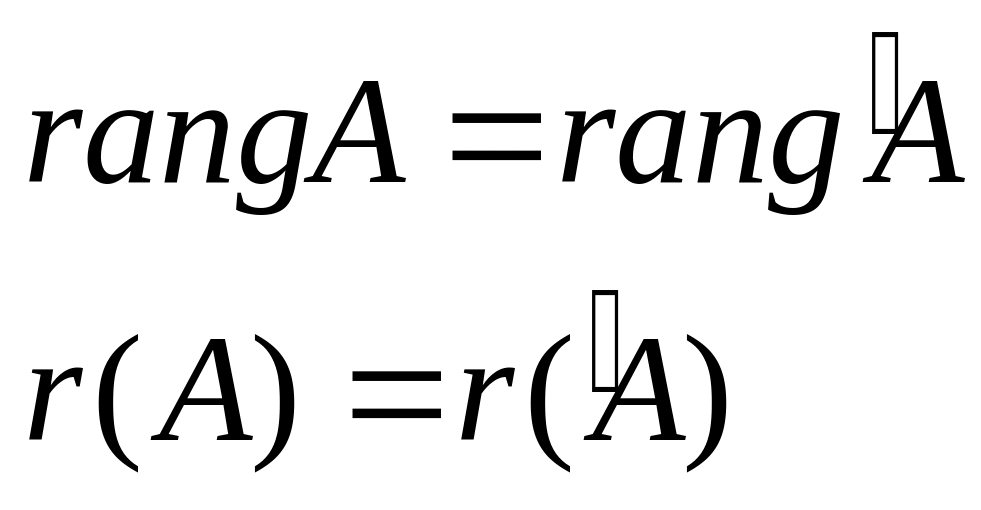
Док-во: ( )  решение (2)

А имеет базисный минор r-го порядка. Любой столбец А представляется в виде линейной комбинации базисных столбцов. Перепишем соотношение (2) в виде:

–

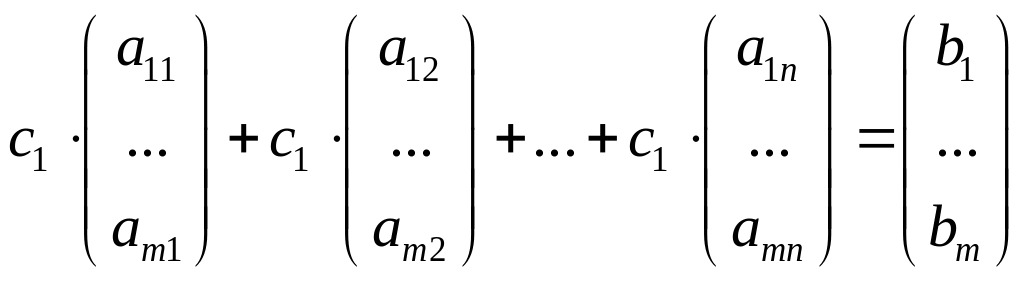
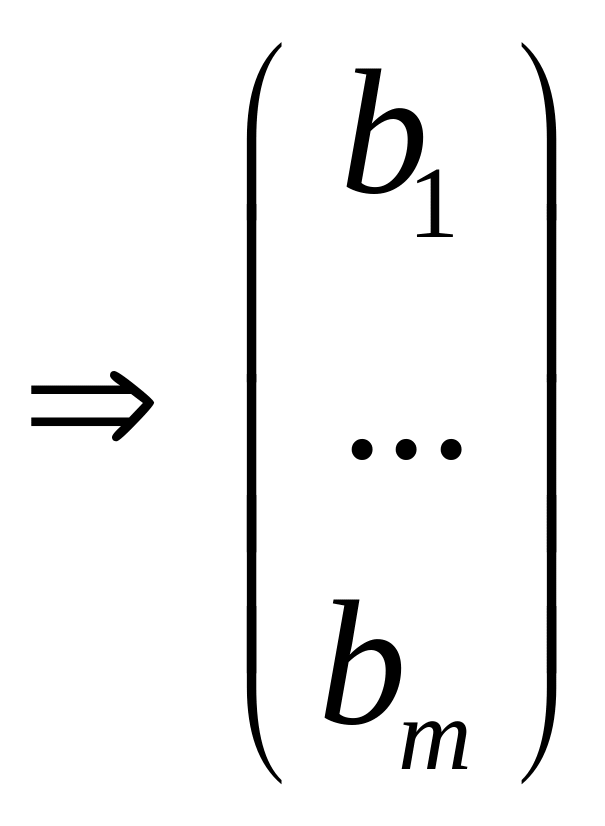линейная комбинация r базисных столбцов максимальное число линейно независимых столбцов . Аналогично в обратную сторону.

Решение по формулам Крамера.

Метод применяется в случае квадратной СЛАУ:

Если определитель , то система n-го порядка имеет единственное решение, которое дается в формуле Крамера (в терминах элементов): ,

– определитель, полученный из основного путем замены j-го столбца столбцом из правой части В.

Док-во:

(для n = 3) Умножим на и складываем правые и левые части:

Аналогично для .

=>  A^-1 => X=A^-1B – формула Крамера в терминах матричного представления.

Метод Гаусса (метод последовательных исключения).

Не обязательно det0, не обязательно квадратные матрицы. Расширенную матрицу приводим к треугольному виду с единицами на главной диагонали путем элементарных преобразований строк (не столбцов). Элементарные преобразования – 1) перестановка любых двух строк (столбцов); 2) умножение любой строки (столбца) на любое число, не равного 0; 3) умножение любой строки (столбца) на любое число и прибавление полученного результата к любой строке (столбцу).

На каждом этапе исключаются некоторые переменные (отсюда название метода).

И потом обратный ход: с конца подставляем решение в предыдущую строку.

Пример

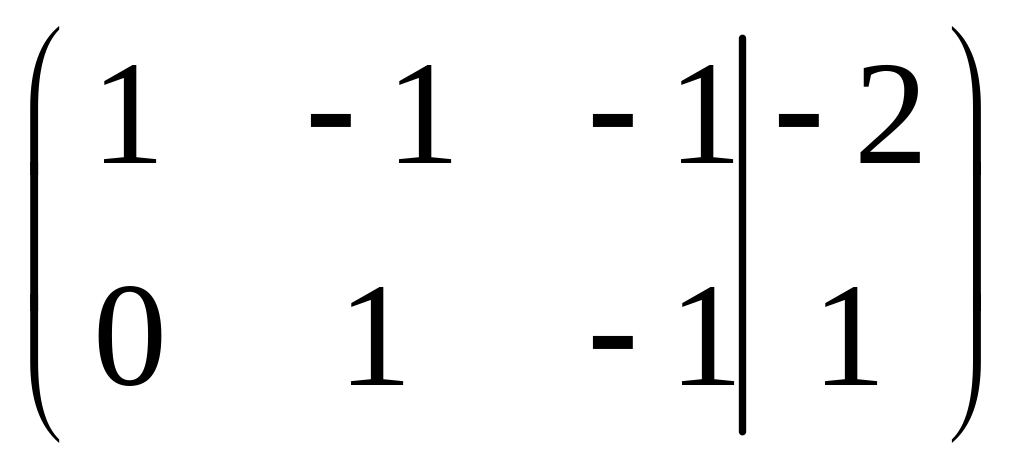– «укороченная» система

Фундаментальная система решения однородной системы.

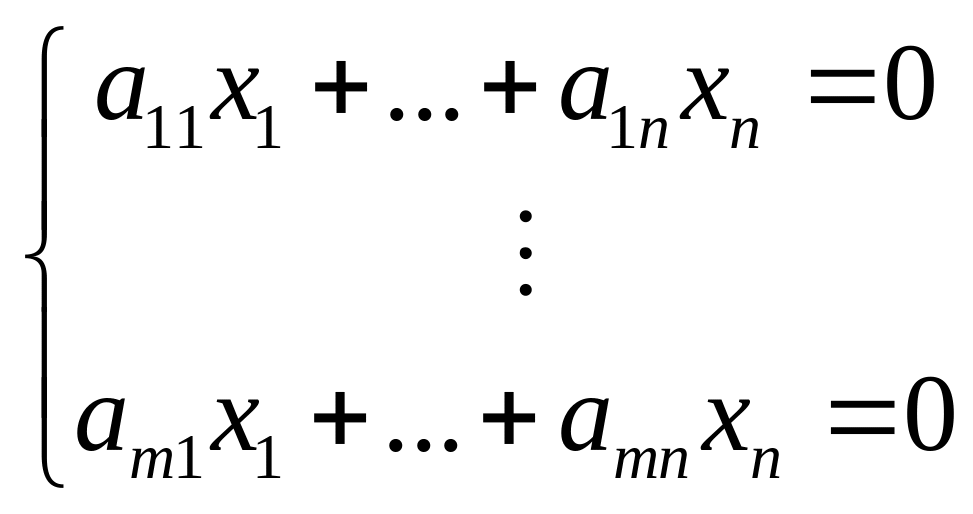(2), АХ=0,

, т.к. В = 0. => (2) всегда имеет решение, т.е. совместна по теореме Кронекера-Капелли.

Если r = n => существует единственное нулевое решение по теореме Крамера, так как все . Если r < n => k = n-r – число свобод неизвестных.

Множество решений системы (2) образует подпространство пространства R_n:

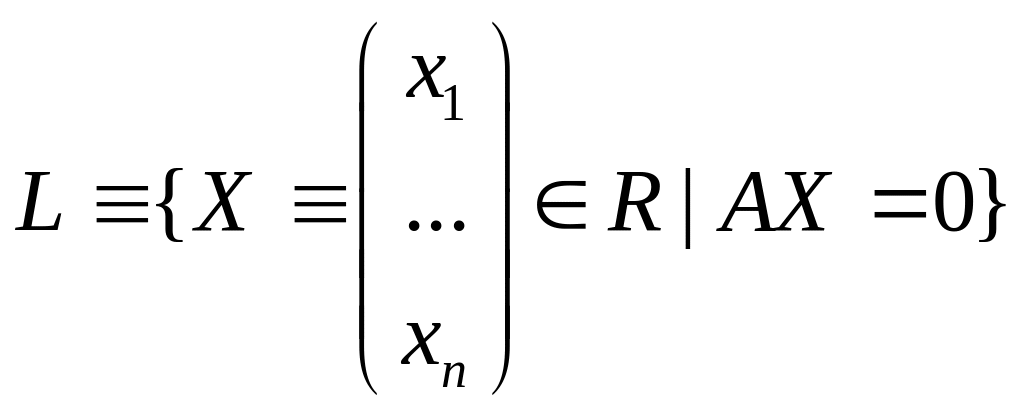
– ВП, поэтому (аксиомы проверять не надо) надо проверить лишь:

L – ВП, его размерность = k => достаточно найти k линейно независимых частных решений, т.е. фундаментальную систему решения. ФСР является базисом подмножества решений однородной системы (2) Если – базис, то общее решение есть линейная комбинация этих (свободных) элементов: .ФСР показывает применение понятия базиса в теории СЛАУ.

Пр. 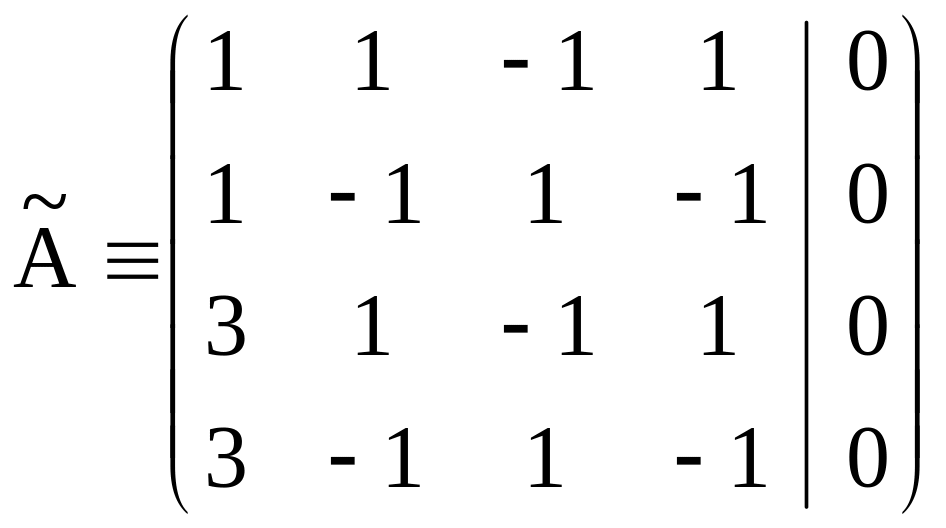r=2, k=4-2=2.Исходная система ~

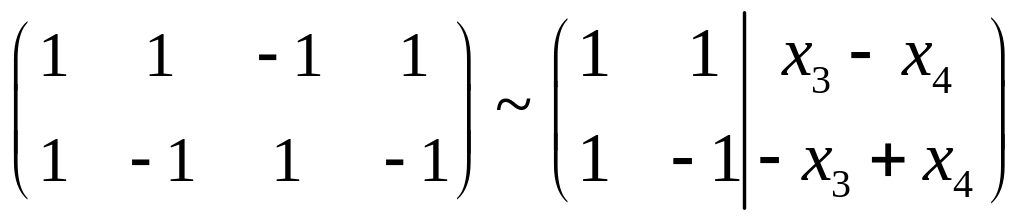
1. x₃=1, x₄=0 => x₁=0, x2=1 => f₁ = (0,1,1,0). 2. x₃=0, x₄=1 => x₁=0, x₂=-1 => f₂ = (0,-1,0,1).

f₁ и f₂ независимы, т.к. det 0, существует минор II порядка отличный от 0. {f₁, f₂} – базис или фундаментальная система решений. Общее решение:

4. Линейные пространства. Аксиоматика, примеры (линейные пространства строк из n чисел, т*n-матриц, непрерывных на отрезке функций). Размерность, базис и система координат в Rⁿ разложение по базису. Евклидово пространство.

Векторное (линейное) пространство

Непустое множество элементов называется векторным пространством над полем (лямбда), если выполняется следующие аксиомы:

I. V – абелева (коммутативная) группа относительно операции сложения. Означает, что определена операция сложения: (декартово произведение)

любой паре (х, у) ставится в соответствие элемент z = x + y, обладающий свойствами

1 х + у = у + х (коммутативность)

2 (х + у) + z = x + (y + z) (ассоциативность)

3 аксиома нуля   V: x +  = x

4  x  V,  (-x) V: x + (-x) = .

(-x – противоположный к x)

V является коммутативной группой по операциям сложения.

II. пусть – поле скаляров (R – вещественное, С – комплексные)

и определены операции умножения:

Выполняются аксиомы:

5 (х) = ()х (ассоциативность)

6 ( + )х = х + х (дистрибутивность относительно скаляра)

7 (х + у) = х + у (дистрибутивность относительно множества)

, то ВП называется вещественным (ВВП)

, то ВП называется комплексным (СВП)

В любом ВП:

1)

2)

Зам. как следствие вытекает из 1-2 свойство 1x=x

Рассмотрим на конкретных примерах:

1. – пространство строк из n чисел

x+y(x₁+y₁,…,x_n+y_n),

x=(x₁,…, x_n),

=(0,…,0) (=x),

(-x)=(-1)x=(-x₁,…,-x_n) => вещественное пространство является векторным.

2. M_nxm– множество всех матриц размерности nm с обычными операциями сложения и умножения на число.

– нулевая матрица,

0=А+(-1)А => M_nxm – векторное пространство.

3. C[a,b]– множество всех непрерывных на [a,b] функций (линейных и нелинейных) с обычными линейными операциями.

Нулевой элемент = 0 – постоянная функция .

Противоположный элемент -f(x) – противоположная функция

-f=-f(x)=-1 f(x)= -f(x) => V – ВВП.

Размерность ВП

ВП V называется n-мерным, если в этом пространстве  хотя бы 1 линейно независимая система из n элементов, а любая система из (n+1) элемента будет линейно зависима.

n называется размерностью и обозначается n = dim V

dim V = max число линейно независимых элементов

Пример

Система линейно независима, если выполняется только когда все ,,…,=0.

Если в V имеется любое число линейно независимых элементов, то оно называется бесконечномерным.

УТВ. dim V = n любые n линейно независимых элементов образуют базис этого пространства.

Базис

Пусть V – ВП

Система называется базисом этого пространства V, если она

1) линейно независима

2) для

(любой элемент представляется как комбинация остальных элементов) – разложение элемента x по базису {e_i} с координатами (x₁,…,x_n), которые определены только в данном базисе.

xV, ! разложение, т.е. координата x_i относительно базиса определяется однозначно.

Док-во: допустим имеется еще одно разложение

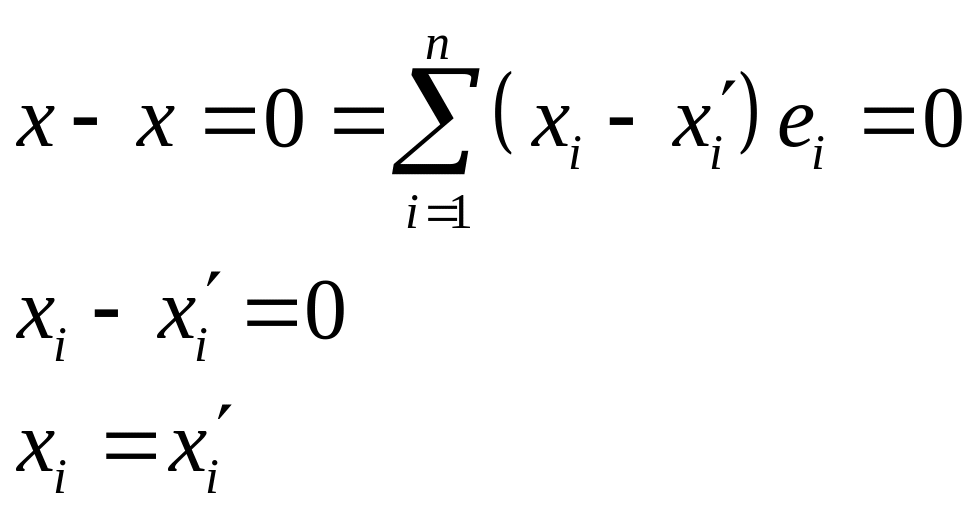
Получили противоречие, ч.т.д.

Пример образует базис.

Численное значение базиса заключается в следующем: линейные операции над элементами сводятся к таким же операциям над обычными числами:

1)

2)

Евклидово пространство – вещественное векторное пространство, для которого:

1. имеется правило

2. скалярное произведение подчинено следующим аксиомам:

1) (x, y) = (y, x) (коммутативность)

2) (x₁ + x₂, y) = (x₁, y) + (x₂, y) (дистрибутивность)

3) (x, y)=(x, y)

4) (х, х) = х² >= 0,

если (х, х) = 0 => х=0.

Свойства ЕП

1 – неравенство Коши-Буняковского.

Пример.

1. V₃- ВП всех геометрических векторов с обычным скалярным произведением 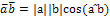. В силу доказанных свойств скалярного умножения, 1-4 имеют место. => данное ВП явл. вещ. ЕП

2. Rⁿ со скалярным произведением 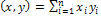. 1-4 выполняется => Rⁿ с указанным произведением является ЕП