Понятие функции комплексной переменной

Комплексные числа мы условились изображать точками плоскости, где задана прямоугольная система координат.

Дадим понятие функции от комплексного переменного.

Пусть даны две плоскости комплексных чисел   и   (рис. 129). Рассмотрим некоторое множество

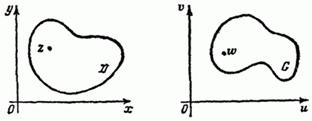
Рис. 129

точек   в плоскости   и множество   в плоскости  . Если каждому числу   по некоторому закону поставлено в соответствие определенное комплексное число  , то говорят, что на множестве   задана однозначная функция комплексного переменного, отображающая множество   в множество  . Символически это обозначают так:

Множество   называют областью определения функции  . Если каждая точка множества   является значением функции, то говорят, что   - область значений этой функции или образ множества   при помощи функции  . В этом случае говорят еще, что функция   отображает   на  .

Функцию   можно записать в виде

         ,

где

,

                     ,

- действительные функции от переменных  .

Если каждому   соответствует несколько разных значений  , то функция   называется многозначной.

Понятия предела и непрерывности функции комплексного переменного вводятся аналогично, как это делается для функции действительного переменного, необходимо лишь всюду вместо абсолютной величины писать модуль комплексного числа.

Говорят, что функция

имеет предел в точке  , равный числу  , если

.                       (1)

В этом случае пишут

.

На языке функций   и   свойство (1) записывается в виде равенства

                   (2)

или, что все равно, в виде двух равенств

,         .                     (3)

Для комплексных функций   и   имеют место свойства, аналогичные соответствующим свойствам действительных функций:

                      (4)

Как обычно, формулы (4) надо понимать в том смысле, что если пределы, стоящие в их правых частях, существуют, то существуют также пределы, стоящие в их левых частях, и выполняется соответствующее равенство.

Функция   называется непрерывной в точке  , если для нее выполняется свойство

,   ,  .                    (5)

Таким образом, непрерывная в точке   функция должна быть определена в окрестности этой точки, в том числе и в ней самой и должно выполняться равенство (5). Равенство (5) эквивалентно двум равенствам:

,  .

Следовательно, непрерывность   в точке   эквивалентна непрерывности функций   и   в точке  .

Из свойств (4) следует, что сумма, разность, произведение и частное непрерывных в точке   комплексных функций  и   есть непрерывная функция в этой точке. В случае частного надо в этой формулировке считать, что  .

Пример 1. Функция   задана на всей комплексной плоскости. Ее значения – неотрицательные числа. Эта функция непрерывна во всех точках комплексной плоскости:

   .

Пример 2.

   .         (6)

Эта функция многозначная (бесконечнозначная);   - главное значение аргумента  .

Пример 3. Функция  . Она непрерывна:

   .

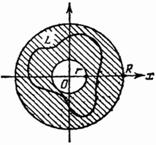
Рис. 130

Но тогда и функция     непрерывна как произведение конечного числа непрерывных функций.

Множество комплексных чисел   будем называть областью, если  , как множество точек плоскости, открыто и связно.

Область   называется односвязной, если любая непрерывная замкнутая самонепересекающаяся кривая, проведенная в  , ограничивает некоторую область  , целиком принадлежащую  . Область, не обладающую этим свойством, будем называть многосвязной.

Пример 4. Кольцо   - многосвязная (двусвязная) область. Кривая   (рис. 130) принадлежит кольцу, но ограничивает область, не входящую целиком в него.

Дополнительно подробно вопрос( Понятие функции комплексной переменной (ФКП). Многозначность ФКП. Основные элементарные ФКП. Основные элементарные ФКП и их геометрические свойства. Предел и непрерывность ФКП.)

Тема № 22. Функция комплексного переменного Определение функции комплексного переменного

        Понятие функции комплексного переменного является частным случаем общего математического понятия функции.

Определение. Если А –  некоторое множество комплексных чисел z (геометрически –  множество точек комплексной плоскости), и каждому числу z А поставлено в соответствие по некоторому закону число w  В (где В –  также множество комплексных чисел), то говорят, что на множестве А определена функция комплексного переменного z (или отображение множества А в В ).

Записывают: w  = f (z).

        Множество А называют областью определения функции, В –  множество, состоящее из значений, принимаемых функцией, называют областью значений функции.

         Принято множества А и В, изображать на отдельных комплексных плоскостях (см. рис. 5): плоскость z комплексных чисел z  = х + i у и плоскость w комплексных чисел w = u + i v .

        При этом точка w₀  = f (z₀) называется образом точки z₀, а z₀–  прообразом точки w₀.

        В частности, если А расположено на действительной оси ох, то z  = х является действительным переменным. Если же все значения w также действительны, то приходим к понятию функции действительного переменного как частному случаю функции комплексного переменного.

В общем случае z  = х + i у, w  = u (х, у) +  i v (х, у).

        Геометрически функцию f (z ) можно рассматривать как отображение множества А на множество В, переводящее точку (х, у) множества А в точку ( u, v ) множества В. Высказывание “ функция w  = f (z) определена на множестве А” эквивалентно следующему: “ каждой точке (х, у) из А поставлены в соответствие действительные числа  u   и v ” . Иными словами, на множестве Аопределены две действительные функции

 и   двух действительных переменных х и у. Итак, задание функции комплексного переменного w  = f (z) равносильно заданию двух функций двух действительных переменных   и   .

        Например, соотношение w = z² = (x +iy)² = x² – y² + i2xy   эквивалентно следующим: u = x² – y², v = 2xy.

Пример 1. Дана функция   f (z) = z³ + i . Найти мнимую и действительную части этой функции.

Решение.  f (z) = (х + i у)³ + i = x³ + 3x²iy + 3x(iy)² + (iy)³ +  i = x³ – 3xy²  + i (3x²y – y³ + 1).

Откуда u(x,y) = x³ – 3xy² , v(x,y) =  3x²y – y³ + 1.

Замечание.

.

П ример 2. Найти образ окружности x² + y² – 3y = 0 (см. рис. 6) при отображении w = 2z + 1.

 

Решение. 1) Выделим действительную и мнимую части функции w :

        Выразим х и у через u и v : .              (_* )

2 ) Подставим выражения (_* ) в уравнение окружности:

или (u - 1)² + (v -3)² = 9. Это и есть уравнение искомого образа (см. рис.7).

Основные элементарные функции комплексного переменного

        Функции комплексного переменного есть естественное распространение в комплексную область обычных для анализа элементарных функций. Однако, при таком распространении функции иногда приобретают новые свойства.

        Например, показательная функция комплексного переменного e^z оказывается периодической, функции sin z   и  cos z   перестают быть ограниченными, приобретают смысл логарифмы отрицательных чисел и т.д.

        Основными элементарными функциями комплексного переменного являются:

1. Степенная функция w = zⁿ.

2. Рациональная функция

а) многочлен w = c₀ + c₁z + c₂z² + ...+ c_nzⁿ;

б) отношение двух многочленов

 –  дробно-рациональная функция.

Пример 3. Найти образ прямой у = - х (см. рис. 8) при отображении   .

Решение. Имеем дробно-рациональную функцию. 1) Преобразуем её, выразив явно z :

.

Два комплексных числа равны, если равны их действительные и мнимые части. Значит:

.

2) Ищем образ прямой у = - х, заменяя х и у через u и v :

,  (u + 2) + (v - 3)² = 18 (см. рис. 9).

 

В комплексной плоскости получили уравнения окружности с центром (- 2, 3) и радиусом  .

Заметим, что на примерах 2 и 3 мы проиллюстрировали замечательное свойство дробно-рациональной функции   (частный случай рациональной функции) отображать окружность в окружность (прямую рассматриваем как окружность с бесконечно большим радиусом).

3. Показательная функция   e^z = e^x (cos y + i sin y).

Из определения показательной функции следует, что она не обращается в нуль ни при какомz . Функция e^z обладает периодом   , так как при изменении z на   значение функции не изменяется. Действительно, 

  .