3.1.1.3. Стержни на упругом основании

Расчетная модель стержня на упругом основании используется в некоторых проектных задачах элементов ракетно-космических изделий, в частности, при рассмотрении вопросов местной устойчивости трехслойных и подкрепленных конструкций.

Наиболее прост расчетный анализ в случае так называемого винклеровского основания, когда распределенная реакция упругого основания в каждой точке пропорциональна поперечному перемещению стержня в этой точке и не зависит от перемещений других участков стержня [7], как это показано на рис. 3.9,а. Реакция упругого основания

q_w = –w, (3.77)

где  – коэффициент жесткости упругого основания или коэффициент постели.

Элементарная работа силы q_w на перемещении точки ее приложения

. (3.78)

Потенциал внешних сил (3.14) определяется формулой

. (3.79)

в которой знаки выбираются в соответствии с общим правилом (1.30).

Если ограничиться при расчете простейшими гипотезами Бернулли, то в соответствии с (3.15) полная потенциальная энергия деформируемого стержня

. (3.80)

Если на балку действуют сосредоточенные силы и моменты, в выражение (3.80) войдут также неинтегральные слагаемые. Так, например, для случая нагружения на правом торце сосредоточенной силой P и изгибающим моментом M, положительные направления которых совпадают с положительными направлениями для w и  (см. рис. 3.9,б), это выражение можно записать следующим образом:

. (3.81)

Вариационное уравнение Лагранжа (1.31) при отсутствии сосредоточенных нагрузок приобретает вид

. (3.82)

После двукратного интегрирования по частям из условия (3.82) нетрудно получить дифференциальное уравнение

. (3.83)

и граничные условия, которые для изображенного на рис. 3.9,б стержня совпадут с условиями (3.20).

Если сечение стержня неизменно по его длине, дифференциальное уравнение приобретает вид

, (3.84)

где

. (3.85)

Общее решение дифференциального уравнения

. (3.86)

Четыре неизвестные константы находятся из граничных условий, соответствующих заданному закреплению и нагружению стержня.

3.1.1.4. Расчет колец

Расчет колец обычно рассматривается в курсе строительной механики, где является одним из центральных разделов. Это связано как с методической значимостью данного вопроса (изучение задач деформирования кольца – ключ к пониманию вопросов статики и устойчивости оболочек), так и с большой практической важностью задачи. Тонкое кольцо, нагруженное системой сил и моментов в своей плоскости – расчетная схема шпангоута, являющегося одним из основных силовых элементов ракетных конструкций [5].

Расчетная схема задачи показана на рис. 3.10,а. Замкнутое кольцо нагружено плоской системой распределенных и сосредоточенных сил и моментов, положительные направления которых указаны на рисунке. Если одна из главных осей кольца также лежит в его плоскости, то можно рассматривать только плоское деформирование.

Следуя [5], положим, что кольцо не закреплено неподвижно, а связано с тонкой обшивкой, которая обеспечивает действие на кольцо уравновешивающей тангенциальной нагрузки

. (3.88)

Величины , и могут быть определены из трех уравнений равновесия кольца (сумма проекций всех сил на вертикальную и горизонтальную оси и сумма моментов относительно центра кольца должны быть равны нулю). В дальнейшем считается, что нагрузка уже включена в число действующих нагрузок, и, таким образом, система действующих на кольцо сил и моментов является самоуравновешенной.

Кольцо рассматривается как стержень малой кривизны (полагается, что радиус R много больше толщины кольца). Для расчета используются гипотезы Бернулли.

Кинематика деформирования оси кольца при изгибе показана на рис. 10,б [5]. Элемент дуги AB, имевший до деформации длину Rd, в деформированном состоянии занимает положение A₁B₁. Перемещения точки A в окружном и радиальном направлении равны соответственно v и w. Окружная координата точки B равна Rd, радиальная – нулю (с точностью до высших порядков малости). Координаты точки B₁ в местной системе координат равны соответственно Rd + v + dv + wd и w + dw – vd. Длина отрезка A₁B₁ равна квадратному корню из суммы квадратов разностей координат. Отношение разностей длин до и после деформирования к исходной длине составляет деформацию оси стержня, для которой получается формула

(3.89)

Если ограничиться первым порядком малости (как обычно делают в задачах статики), то

. (3.90)

Другая важная формула может быть получена из равенства разности радиальных координат точек A₁ и B₁ произведению длины отрезка A₁B₁ на синус угла поворота касательной. В силу гипотез Бернулли угол поворота сечения  равен углу поворота касательной , откуда, ограничившись первым порядком малости, получаем

. (3.91)

В задаче изгиба кольца принято пренебрегать изменением длины его оси (как и для прямых стержней, ось которых является нейтральной линией). Используя условие нерастяжимости оси кольца, получаем связь между радиальным и окружным перемещениями в виде

w = –v,_, (3.92)

а выражение (3.91) – в виде

. (3.93)

Как обычно при использовании гипотез Бернулли, перемещения точек, не лежащих на оси кольца, определяются зависимостями

(3.94)

(координата z отсчитывается от оси кольца).

Деформация точек, не лежащих на оси кольца, аналогично (3.5), равна

. (3.95)

Удельная потенциальная энергия деформаций, связанных с изгибом кольца, аналогично (3.2), равна половине произведения деформации (3.95) на соответствующее ей напряжение, которое по закону Гука равно произведению модуля упругости в окружном направлении E на указанную деформацию (напряженное состояние, как обычно, считается одноосным):

. (3.96)

При расчете колец формулу для потенциальной энергии деформации тела (1.29) удобно записывать в виде, аналогичном (3.12):

. (3.97)

где изгибная жесткость EI определяется согласно (3.9).

Окончательно,

. (3.98)

Потенциал внешних нагрузок, согласно (1.30),

. (3.99)

В последнем выражении величины v_i, w_j и _k суть перемещения и углы поворота точек приложения сил T_⁽ⁱ⁾, T_R^(j) и моментов M^(k) соответственно. Знаки перед членами, содержащими сосредоточенные и распределенные моменты, объясняются выбранными положительными направлениями для моментов и углов поворота сечения.

Вариационное уравнение Лагранжа записывается в виде (1.31); из него следует уравнение Эйлера для кольца с нерастяжимой осью

.(3.100)

Для кольца с постоянной изгибной жесткостью уравнение (3.100) приобретает более простой вид

. (3.101)

Следует обратить внимание на то, что в уравнения (3.100) и (3.101) входит не сама радиальная нагрузка q_R, а ее производная по окружной координате. Между прочим, это означает, что добавление постоянной радиальной нагрузки, действующей по всему периметру кольца, не влияет на его напряженно-деформированное состояние. Это является следствием принятия условия нерастяжимости оси кольца. Поскольку рассматриваемая задача решается в линейной постановке, в случае действия на кольцо постоянной радиальной нагрузки ее можно вычленить в отдельную задачу о равномерном растяжении-сжатии оси кольца и затем произвести суперпозицию полученных решений.

Полученные уравнения шестого порядка нуждаются в шести граничных условиях. Для замкнутого кольца, не закрепленного как жесткое целое, три условия являются условиями замкнутости:

(3.102)

Еще три условия могут быть получены из следующих соображений. Хотя кольцо может смещаться в пространстве как жесткое целое, изгибные перемещения кольца не должны включать в себя этих смещений. Это выражается условием ортогональности функций v() и

v₀() = a₀ + a₁cos + b₁sin (3.103)

(в последнем выражении первый член соответствует повороту кольца, второй и третий – смещению его по горизонтальной и вертикальной осям). Таким образом, три недостающие условия имеют вид

(3.104)

.

Искомая функция v() определяется решением уравнения (3.100) или (3.101) с условиями (3.102) и (3.104). Затем по формуле (3.92) определяются радиальные перемещения w() и углы поворота сечения (). После этого можно найти внутренний изгибающий момент

. (3.105)

Перерезывающие силы Q и нормальные силы N нельзя выразить непосредственно через перемещения, используя закон Гука, поскольку были сделаны допущения о равенстве нулю деформаций оси кольца  и угловых деформаций  (последнее есть следствие гипотезы плоских сечений). Однако, эти силы можно определить из уравнений равновесия элемента кольца, показанного на рис. 3.10,в:

, (3.106)

. (3.107)

Таким образом, нахождение величин w, , M, Q и N сводится к последовательному дифференцированию полученной зависимости v().

Решение уравнений (3.100) и (3.101) может быть произведено различными способами.

В самом общем случае может быть получено численное решение, например, методом конечных элементов. В случае, если правая часть уравнений достаточно проста, можно получить общее решение. Если необходимы только силовые факторы – можно использовать известные из курса сопротивления материалов метод сил для анализа статически неопределимых систем [14]. Наконец, для колец с постоянной изгибной жесткостью, если интерес представляют в первую очередь зависимости для перемещений и углов поворота, – имеет смысл искать решение в тригонометрических рядах. Остановимся подробнее на этом последнем случае.

Окружные перемещения точек оси кольца могут быть записаны в виде ряда Фурье, удовлетворяющего условиям замкнутости кольца (3.102)

. (3.108)

Следует обратить внимание на то, что в выражении (3.108) отсутствует свободный член, а суммирование начинается не с единицы, а с двух. Это связано с отсутствием в исследуемом решении перемещений кольца как жесткого целого (3.103).

Выражение (3.99) после подстановки в него (3.108) с учетом (3.92), (3.93) и условий равновесия кольца как жесткого целого приобретает вид [5]

. (3.109)

В последнем выражении обозначено

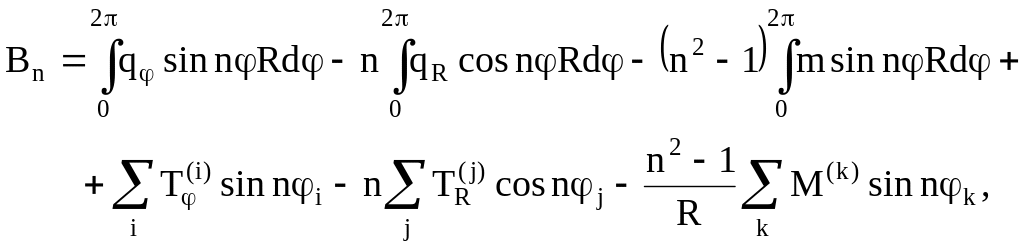^(3.110)

где _i, _j и _k – угловые координаты точек приложения сил T_⁽ⁱ⁾, T_R^(j) и моментов M^(k) соответственно. Знаки указаны для положительных направлений силовых факторов, изображенных на рис. 10.

Потенциальная энергия деформированного кольца (3.98) после подстановки (3.108) может быть представлена в виде

(3.110a)

Для кольца постоянной жесткости в силу ортогональности тригонометрических функций последнее выражение может быть преобразовано к виду

. (3.110b)

Коэффициенты ряда (3.108) могут быть получены из уравнений

(3.110c)

Для колец постоянной изгибной жесткости с учетом (3.110b) система уравнений (3.110c) распадается на отдельные уравнения для каждого коэффициента ряда (3.108). Таким образом, последние могут быть вычислены по формулам [5]

(3.111)

Таким образом, с учетом (3.92), (3.93), (3.105), (3.106) и (3.107) могут быть записаны следующие зависимости:

^(3.112)

На первый взгляд, получено полное решение задачи. Однако следует помнить, что сходимость рядов, получаемых последовательным дифференцированием, неуклонно ухудшается. Если ряды для перемещений сходятся очень быстро, то уже ряд для моментов может быть расходящимся (если в числе внешних нагрузок присутствуют сосредоточенные или распределенные моменты), а ряды для внутренних сил, как правило, расходятся. Это и определяет ограниченную область применения данного расчетного метода.

В качестве примера можно привести расчет перемещений шпангоута разгонного блока, к которому на стержнях крепится ракетный двигатель, как это показано на рис. 3.11. В данном случае представляла интерес не прочность шпангоута, а локальные окружные деформации в местах приложения сил, которые могли привести к разрушению тонкой композитной оболочки, соединенной со шпангоутом.

Восемь радиальных сосредоточенных сил в соответствии с (3.110) соответствуют коэффициентам

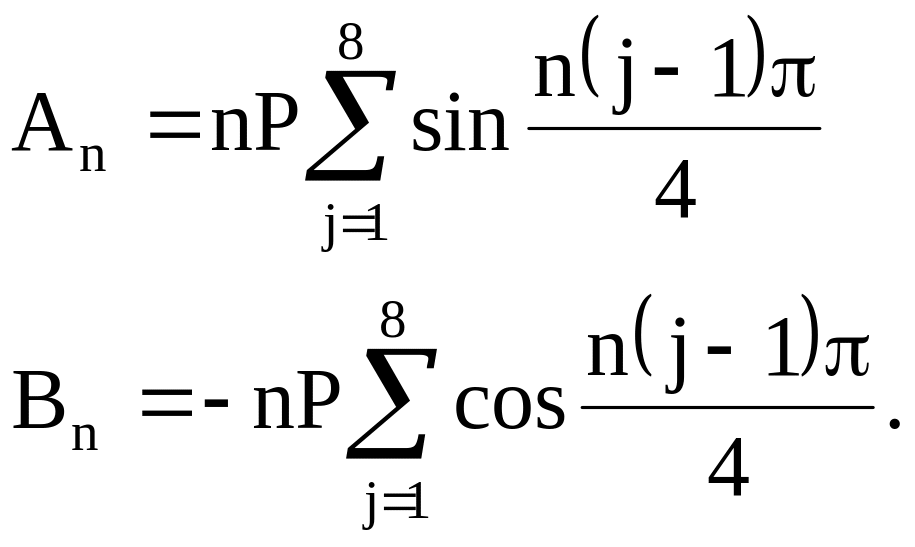(3.113)

Ряды для перемещений сходятся очень быстро, достаточно нескольких первых членов. На рис. 3.11 приведена зависимость радиальных перемещений от угловой координаты. Максимальное радиальное перемещение, определение которого и являлось целью данного расчета, составляет

(3.113а)

Ряд (3.113а) сходится очень быстро, и для оценки максимального прогиба достаточно нескольких первых его членов.