3.1.1.2. Трехслойные балки с легким заполнителем

Расчетная схема трехслойной балки также может быть проиллюстрирована рисунком 3.1. Особенность данного класса конструкций – трехслойная структура, описанная в разделе 2.3 и показанная на рис. 2.5. Каждая из обшивок представляет собой многослойную полоску шириной b, а заполнитель – слой толщиной 2c, для которого справедливо условие (2.6). В направлении оси z заполнитель считается несжимаемым. Характеристики обшивок и заполнителя неизменны по длине стержня.

Расчет трехслойных конструкций может проводиться на основе различных кинематических гипотез. Наиболее распространенными из них являются [3, 19]:

• расчет по гипотезам Бернулли для всего трехслойного пакета;

• расчетная схема с учетом сдвига в заполнителе и мембранного деформирования обшивок;

• расчетная схема "ломаной линии", при которой учитывается сдвиг в заполнителе, а для каждой из обшивок считаются справедливыми гипотезы Бернулли.

Перечисленные расчетные схемы показаны на рис. 3.6.

При расчете с использованием гипотез Бернулли для всего трехслойного пакета могут быть использованы формулы, приведенные в п. 3.1.1.1. При расчете изгибной жесткости сечения следует принять нулевое значение модуля упругости заполнителя. Практические расчеты показывают, что для достаточно длинных балок с типичными заполнителями использование гипотез Бернулли возможно для приближенных оценок.

При расчете с учетом сдвига в заполнителе и мембранного деформирования обшивок деформированное состояние стержня описывается двумя независимыми функциями: поперечным перемещением точек нейтральной линии w(x) и углом поворота заполнителя (x). Перемещения и деформации в пределах каждой обшивки считаются постоянными и равными перемещениям и деформациям поверхности контакта заполнителя с соответствующей обшивкой. Это допущение может быть справедливым для тонких (в сравнении с высотой трехслойного пакета) обшивок, слабо сопротивляющихся изгибу. Таким образом, условием применимости данной расчетной схемы является

2c >> H. (3.48)

Перемещения в обшивках трехслойного стержня

u_1,2 = c (3.49)

w_1,2 = w,

где w – поперечное перемещение срединной линии; знак плюс относится к нижней обшивке (1), минус – к верхней (2), как это показано на рис. 3.6,б.

Деформации в обшивках

_1,2 = с,_x. (3.50)

Деформация сдвига заполнителя согласно схеме Тимошенко определяется зависимостью

_xz^(з) =  – w,_x. (3.51)

Потенциальная энергия деформирования стержня U определяется суммой энергии растяжения-сжатия обшивок и сдвига заполнителя:

, (3.52)

где E_x – средний модуль упругости многослойной обшивки в продольном направлении, определяемый согласно (1.18) или (1.20), G_xz⁽³⁾ – модуль сдвига заполнителя в продольной плоскости, который рассчитывается по формуле

G_xz⁽³⁾ = G₁₃⁽³⁾cos²₃ + G₂₃⁽³⁾sin²₃. (3.53)

В последнем выражении величины G₁₃⁽³⁾ и G₂₃⁽³⁾ суть модули сдвига заполнителя в его естественной системе координат (см. таблицу 2.3), ₃ – угол поворота заполнителя относительно продольной оси x стержня.

Выражение (3.52) можно записать в виде

, (3.54)

где EI и GF – изгибная и сдвиговая жесткости трехслойного стержня:

EI = 2bHc²E_x,

GF = 2bc G_xz⁽³⁾. (3.55)

При нагружении балки поперечной нагрузкой q вариационное уравнение Лагранжа с учетом обозначений (3.55) совпадает с выражением (3.32). Следовательно, для решения этого уравнения могут быть использованы зависимости (3.33)(3.38). Так, например, при изгибе шарнирно закрепленной по обоим концам трехслойной балки, нагруженной постоянной распределенной нагрузкой q (рис. 3.3,б), решение имеет вид

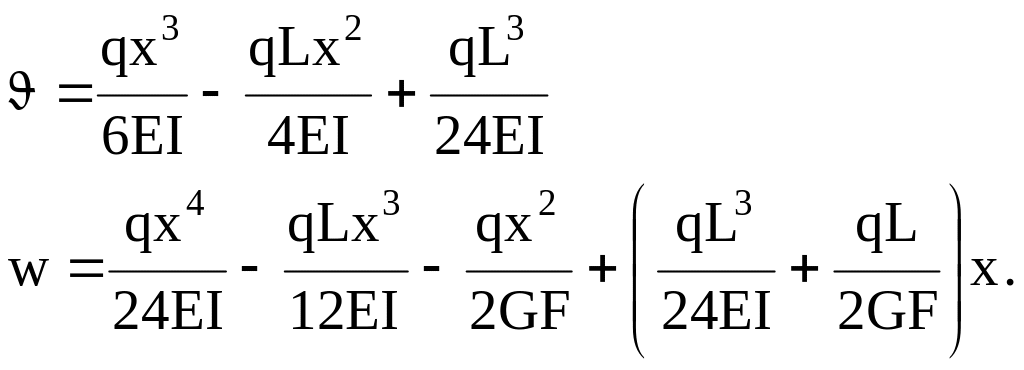(3.56)

Максимальное перемещение имеет место в середине балки и равно

. (3.57)

Сопоставляя полученное решение с выражениями (3.24), нетрудно убедиться, что необходимость учета сдвиговой податливости заполнителя и в этом случае определяется величиной поправки Тимошенко.

При расчете по гипотезе "ломаной линии" полагается, что каждая из обшивок изгибается в соответствии с гипотезами Бернулли, а связывающий их заполнитель деформируется при этом по схеме Тимошенко. Такая расчетная схема свободна от допущения (3.48).

Деформированное состояние стержня по-прежнему описывается двумя независимыми функциями: поперечным перемещением координатной поверхности w(x) и углом поворота заполнителя (x).

Перемещения в обшивках

u_1,2 = –zw,_x  c( – w,_x)

w_1,2 = w, ^(3.58)

где w – поперечное перемещение срединной линии; знак плюс относится к нижней обшивке (1), минус – к верхней (2), как это показано на рис. 3.6,в.

Деформации в обшивках

_1,2 = –zw,_xx с(,_x – w,_xx). (3.59)

Деформация сдвига в заполнителе согласно схеме Тимошенко определяется зависимостью (3.51).

Потенциальная энергия деформирования стержня

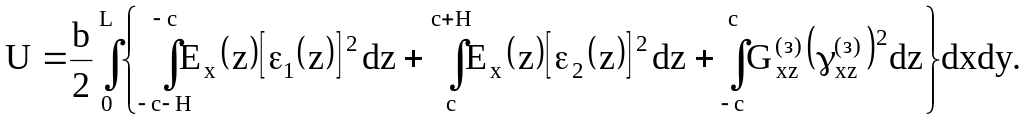(3.60)

В выражении (3.60) в первый интеграл должно подставляться выражение (3.59), соответствующее нижней обшивке (со знаком плюс), а во второй – верхней (со знаком минус).

С учетом (3.59) и (3.51) потенциальная энергия при изгибе трехслойного стержня может быть записана в виде

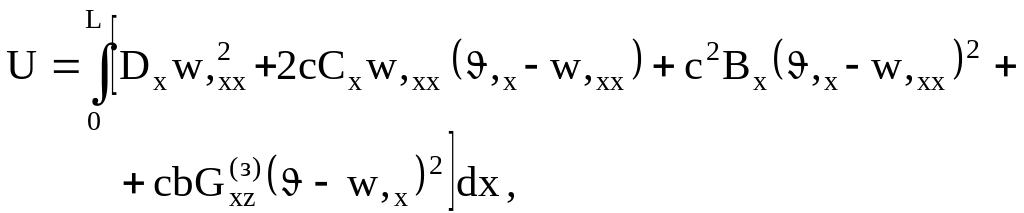(3.61)

где обозначено

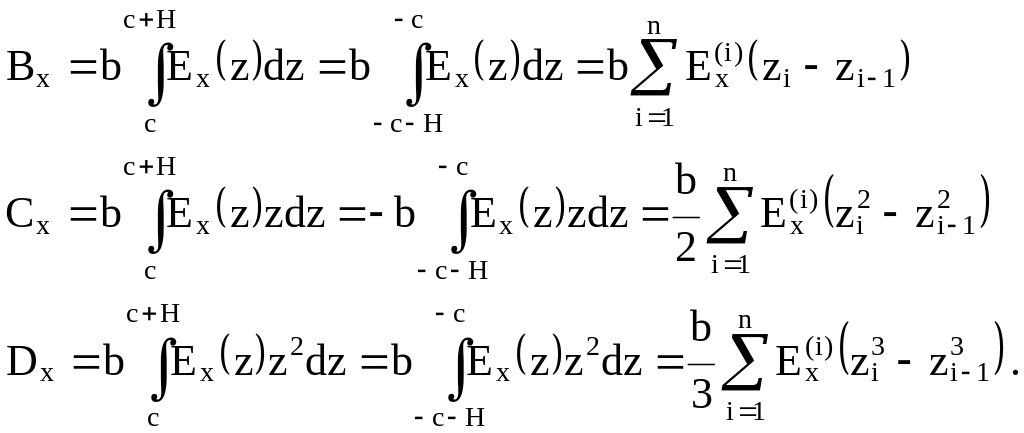(3.62)

Суммы в (3.59) вычисляются для одной обшивки (верхней), при этом отсчет координаты z ведется от срединной поверхности заполнителя. Нумерация слоев обшивки ведется от ее внутренней (смежной с заполнителем) поверхности.

Изгибающий момент и перерезывающая сила с учетом (3.59) могут быть определены по формулам

, (3.63)

. (3.64)

При нагружении балки поперечной нагрузкой q вариационное уравнение Лагранжа имеет вид

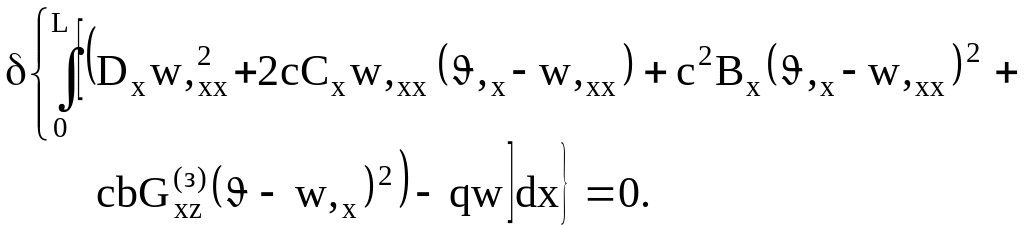(3.65)

Наиболее простой вид разрешающих уравнений и граничных условий можно получить, если провести в выражении (3.61) замену переменной, введя величину s = c( – w,_x), пропорциональную деформации сдвига заполнителя _xz согласно (3.51). В этом случае вариационное уравнение (3.65) приобретает вид

(3.66)

После двукратного интегрирования по частям

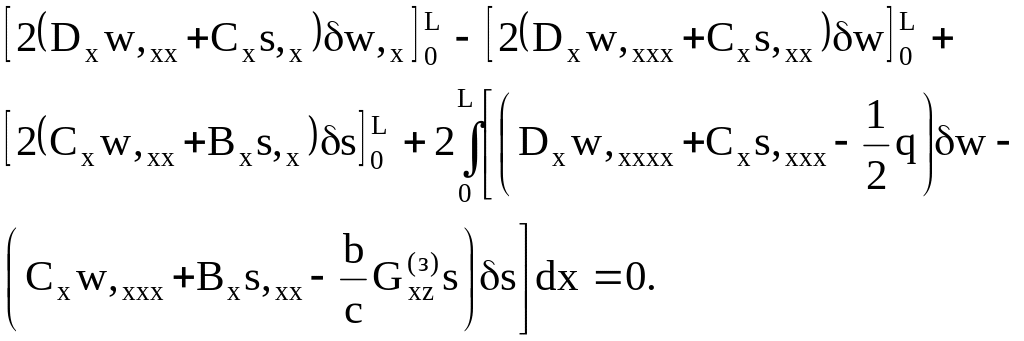(3.67)

Из условия (3.65) следуют уравнения

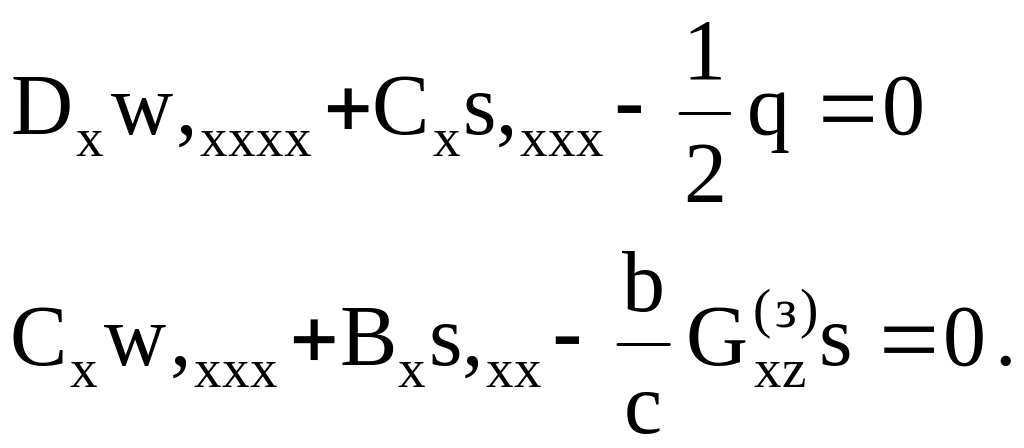(3.68)

и граничные условия, определяемые равенством нулю внеинтегральных слагаемых. Граничные условия в данном случае оказываются дополнены еще двумя выражениями, определяющими связь между обшивками на концах трехслойной балки (наличие или отсутствие диафрагмы на каждом торце [19]).

Для понимания этих граничных условий стоит заметить, что, в соответствии с (3.63) и (3.64), сомножитель при величине w,_x в первой квадратной скобке представляет собой внутренний изгибающий момент М_x, а сомножитель при величине w во второй квадратной скобке – перерезывающую силу. Что касается третьей пары граничных условий, то возможное условие s = 0 может быть выполнено при  = w,_x, то есть, при наличии диафрагмы на торце стержня. Если такая диафрагма отсутствует, и угол поворота заполнителя может отличаться от угла поворота обшивок, то необходимо выполнение условия C_xw,_xx + B_xs,_x = 0. При наличии сосредоточенных сил они войдут в граничные условия аналогично тому, как было рассмотрено выше.

Систему (3.68) несложно преобразовать к уравнениям, разрешенным относительно каждой из неизвестных функций:

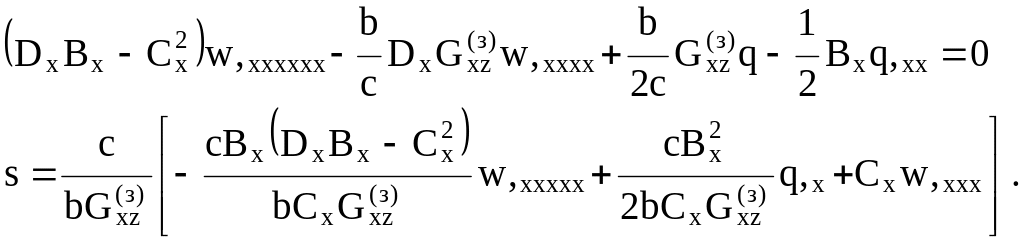(3.69)

Система уравнений (3.69) существенно сложнее, чем соотношения (3.36), справедливые для случая мембранного деформирования обшивок. Тем не менее, в случае q = const может быть получено общее решение этой системы в виде

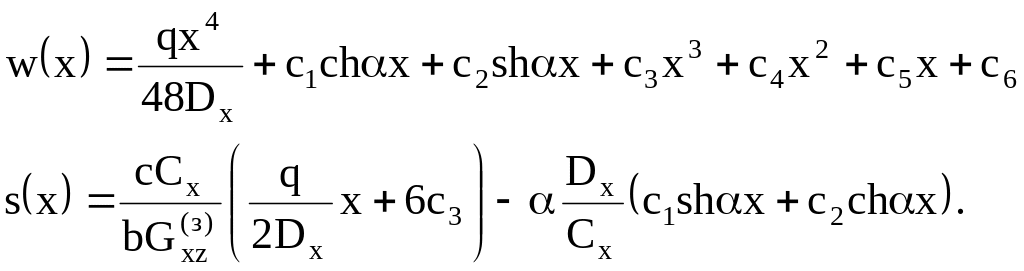(3.70)

где

. (3.71)

Для шарнирно опертого стержня, изображенного на рис. 3.3,б, решение задачи при отсутствии диафрагм на торцах имеет вид

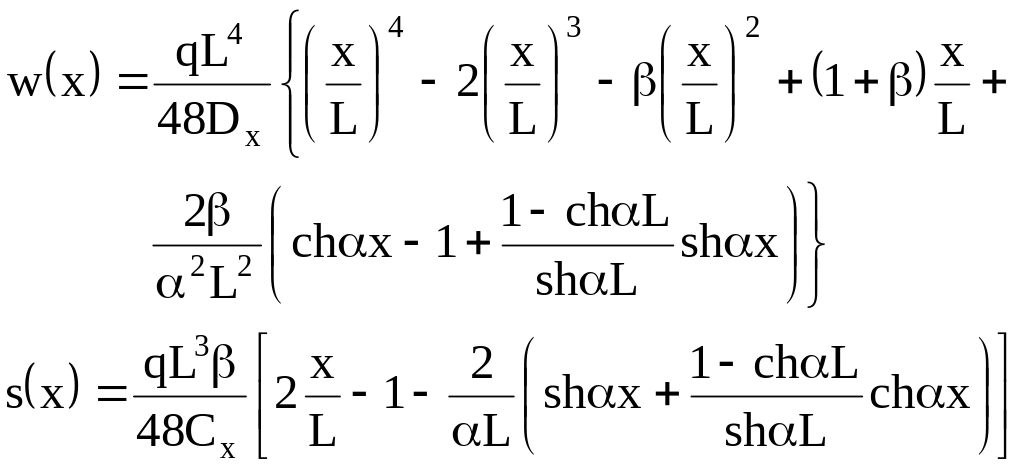_(3.72)

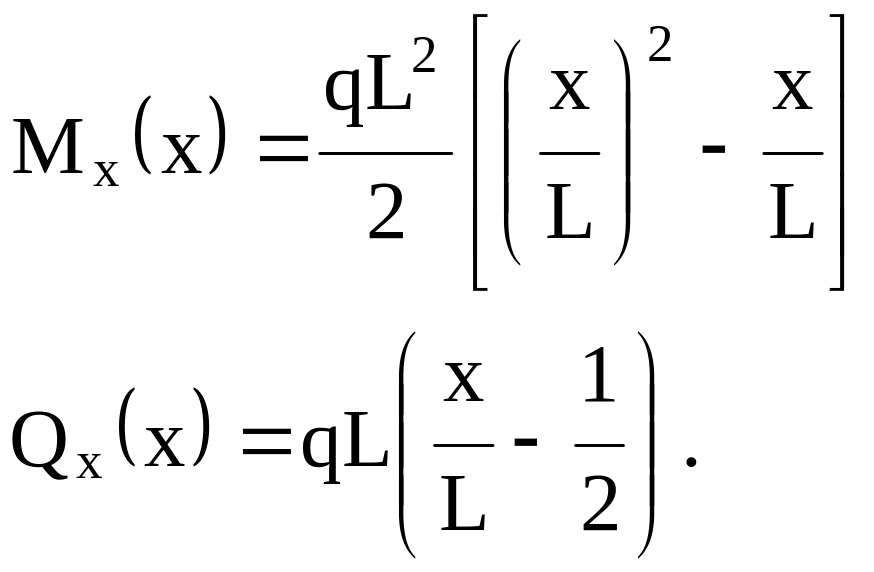
где

. (3.73)

Если обшивки на торцах соединены между собой жесткой связью (s(0) = 0 и s(L) = 0), то вместо первых двух уравнений (3.72) справедливо

(3.74)

(уравнения для момента и силы в статически определимой системе не зависят от наличия связи между обшивками на торцах).

Максимальный прогиб в середине стержня в первом случае равен

. (3.75)

а во втором –

. (3.76)

Стоит заметить, что наличие связи на торцах повышает жесткость системы, и, тем самым, приводит к уменьшению максимального прогиба под нагрузкой. Интересно также сопоставить полученные зависимости с выражением (3.57), справедливым для тонких обшивок, когда выполняется условие (3.48).

Рис. 3.7 и 3.8 показывают типичные зависимости для перемещений и максимальных напряжений в шарнирно опертом стержне, изображенном на рис. 3.3,б, вычисленные при различных кинематических гипотезах.

На первом графике приведены величины безразмерного относительного максимального прогиба в зависимости от отношения H/c. При расчетах считалось, что обшивки однородны по толщине; соотношение E_x/G_xz^(з) принималось равным 500 (примерно соответствует комбинации перекрестно армированной обшивки из углепластика ЛУ-П/ЭНФБ с углом армирования 20 с сотовым заполнителем АМг-2Н 2,5/0,03), а соотношение L/c – равным 20 и 100.

Видно, что для достаточно длинной балки все расчетные схемы приводят к примерно одинаковому результату (при этом линии, иллюстрирующие расчет с диафрагмами и без диафрагм, на графике сливаются в одну). Для коротких балок расчет по гипотезам Бернулли дает сильно заниженные значения перемещений, а расчет по схеме с мембранным деформированием обшивок – несколько завышенные. При c/H > 1520 перемещения, рассчитанные по схеме с мембранным деформированием обшивок и гипотезе ломаной линии, очень близки даже для коротких балок.

Напряжения в обшивках определялись по формулам (3.7) с учетом (3.6), (3.50) и (3.59). На рис. 3.8 показаны напряжения на внешней поверхности однородных обшивок в центральном сечении балки с E_x/G_xz^(з) = 500 при L/c = 20 и 100. Как показывают расчеты, для длинных балок все расчетные схемы приводят к почти одинаковым величинам напряжений; для коротких балок схема ломаной линии дает несколько большие значения напряжений, чем прочие расчетные гипотезы.

Следует заметить, что использование выражений (3.69) или (3.70) вместо (3.36) и (3.37) с учетом (3.55) не всегда приводит к повышению точности расчетов. Это связано с уже упоминавшимся эффектом Пуассона для слоев многослойных полосок, которыми являются обшивки трехслойного стержня. При расчете среднего модуля упругости, подставляемого в (3.55), учитывается совместность деформаций слоев в поперечном направлении, тогда как расчет жесткостей обшивки по формулам (3.62) содержит методическую ошибку, связанную с неучетом поперечных напряжений. Поэтому для корректного описания изгиба трехслойных стержней с многослойными обшивками в случае, если толщина заполнителя не слишком мала, следует все же рекомендовать схему расчета с учетом сдвига в заполнителе и мембранного деформирования обшивок.