Расчетные зависимости для композитных элементов несущих конструкций

Постановки задач оптимального проектирования элементов несущих конструкций, как правило, достаточно просты. Обычно в таких задачах имеется два основных критерия качества – минимум массы и максимум несущей способности. Кроме того, могут присутствовать ограничения по жесткости, собственным частотам и иным характеристикам конструкции.

Масса конструкции представляет собой простую функцию от вектора варьируемых параметров (1.1), которая, как правило, может быть записана в аналитическом виде G(X).

Несущая способность конструкции как критерий оптимизации имеет свои особенности. Отчасти мы уже сталкивались с ними при исследовании аналитических решений оптимизационных задач [1]. Как правило, несущая способность представляет собой составную функцию, определяемую наименьшим из нескольких значений, отвечающих различным механизмам исчерпания несущей способности:

P_пред(X) = min {P_пр(X), P_уст^(об)(X), P_уст^(м)(X), P_с.р.(X)}. (3.1)

Предельная нагрузка по критерию прочности P_пр определяется максимальными напряжениями в наиболее опасных точках, которые может выдержать материал данной конструкции. Для вычисления этой величины необходимо определить поле напряжений, а затем провести анализ прочности многослойного пакета. Методики расчетов на прочность были рассмотрены нами ранее [2]; ниже они будут дополнены на случай термосиловых нагрузок.

Предельные нагрузки по критериям общей и местной устойчивости P_уст^(об) и P_уст^(м) определяются из расчетов на устойчивость. Под общей устойчивостью обычно понимают устойчивость конструкции в целом, а под местной – устойчивость отдельных ее элементов. Многие конструкции имеют несколько различных механизмов местной потери устойчивости, так что при оптимизационных расчетах величина P_уст^(м) также может выбираться наименьшей из нескольких различных критериев.

Алгоритм расчета предельных нагрузок по критерию специфических механизмов разрушения композитов P_с.р. также разрабатывается для каждой конкретной композитной конструкции. Обычно такие механизмы связаны с расслаиванием; примером здесь может служить разрушение однонаправленных композитных труб по форме «китайского фонарика» [1].

При необходимости максимизации критерия (3.1) возникает задача равномерной оптимизации или оптимизации по Чебышеву, когда на каждом шаге поиска отыскивается возможность увеличения наименьшей из нескольких функций, так что в результате все они более или менее равномерно возрастают. Если критерий (3.1) используется как ограничение (например, при минимизации массы), то необходимо, чтобы величина наименьшей из входящих в него функций была не менее уровня действующих нагрузок.

Поскольку нагрузки могут задаваться в нескольких расчетных случаях, максимизируемый критерий или критерий-ограничение дополняются функциями, описывающими исчерпание несущей способности конструкции во всех этих случаях.

Задачи статики

3.1.1. Перемещения, деформации и напряжения при изгибе стержней

3.1.1.1. Многослойные композитные балки

Расчетная схема изгибаемой балки показана на рис. 3.1. Функция w(x) определяет перемещение в направлении оси z точек нейтральной линии (для многослойной полоски положение нейтральной линии определяется условием (2.4), для прочих профилей, приведенных в таблице 2.1, могут быть использованы обычные формулы сопротивления материалов [14]).

Расчет композитных балок может проводиться с использованием различных кинематических гипотез, наиболее употребительными из них являются гипотезы Бернулли и гипотезы Тимошенко.

Гипотезы Бернулли, известные из курса сопротивления материалов, включают гипотезу плоских сечений и условие ненадавливания слоев. Эти гипотезы позволяют упростить выражение (1.11): первая из них означает равенство нулю деформации _xz (поскольку прямой угол в плоскости xz остается прямым), а вторая позволяет пренебречь произведением _z_z. Рассматривая только силовые факторы, действующие в плоскости изгиба xz, окончательно получим

. (3.2)

Схема деформирования стержня в соответствии с гипотезами Бернулли показана на рис. 3.2,а. Перемещения всех точек стержня в этом случае полностью определяются одной функцией w(x). Перемещения в направлении оси x определяются только поворотом сечений; при малых углах поворота сечения  справедливо

u(z) = –z. (3.3)

В свою очередь, угол поворота сечения равен углу поворота касательной:

 = w,_x. (3.4)

В соответствии с (1.7) определяется линейная деформация в направлении оси стержня

_x = u,_x = –z,_x. (3.5)

В силу гипотезы плоских сечений

_x = –zw,_xx. (3.6)

Поскольку напряженное состояние считается одноосным, закон Гука записывается в виде

_x = E_x_x, (3.7)

где E_x – модуль упругости в направлении оси стержня в текущей точке (в общем случае это функция от координат x и z).

Распределение напряжений _x по координате z определяется линейной (для многослойной полоски – кусочно-линейной) функцией и статически эквивалентно изгибающему моменту

. (3.8)

В последнем выражении изгибная жесткость EI есть интеграл по площади сечения S от произведения модуля упругости на квадрат расстояния до нейтральной линии:

. (3.9)

Величины изгибных жесткостей типичных многослойных профилей приведены в таблице 2.1.

Как следует из уравнений равновесия элемента стержня [14], перерезывающая сила равна первой производной от выражения (3.9) по продольной координате:

. (3.10)

Таким образом, выражение (3.2) приобретает вид

. (3.11)

Проинтегрировав последнее выражение по объему стержня, можно записать

, (3.12)

где L – длина стержня.

Потенциал внешних сил (1.30) в данном случае определяется формулой

. (3.14)

Полная потенциальная энергия деформируемого стержня

. (3.15)

Если на балку действуют сосредоточенные силы и моменты, в выражение (3.15) войдут также внеинтегральные слагаемые. Так, например, для случая нагружения на правом торце сосредоточенной силой P и изгибающим моментом M, положительные направления которых совпадают с положительными направлениями для w и  (см. рис. 3.3,а), это выражение можно записать следующим образом:

. (3.16)

Вариационное уравнение Лагранжа (1.31) при отсутствии сосредоточенных силовых факторов приобретает вид

. (3.17)

После двукратного интегрирования по частям

. (3.18)

Поскольку в положении равновесия условие (3.18) должно выполняться при любых допустимых вариациях прогиба w, из этого условия следуют дифференциальное уравнение изгиба стержня и естественные граничные условия. Дифференциальное уравнение для функции w(x) имеет вид

. (3.19)

К уравнению четверного порядка прилагаются четыре граничные условия на торцах стержня (при x = 0 и x = L), которые могут быть следующими.

1. Либо EIw,_xx = 0, либо w,_x = 0 (последнее условие означает, что задана величина w,_x; например, w,_x = 0).

2. Либо (EIw,_xx),_x = 0, либо w = 0 (последнее условие означает, что задана величина w; например, w = 0).

С учетом (3.8) и (3.10) эти граничные условия могут быть сформулированы для внутренних силовых факторов M_x и Q_x:

1. Либо M_x = 0, либо задана величина w,_x.

2. Либо Q_x = 0, либо задана величина w.

Если к торцам стержня приложены сосредоточенные нагрузки, они войдут в граничные условия. Так, например, для изображенного на рис. 3.3,а стержня, для которого справедливо (3.16), граничные условия имеют вид

w|_x = 0 = 0

w,_x|_x = 0 = 0

[EIw,_xx – M]_x = L = 0 (3.20)

[(EIw,_xx),_x + P]_x = L = 0.

Дальнейшее решение проводится в зависимости от вида функций q(x) и EI(x) в конкретных задачах. После нахождения зависимости w(x) по формулам (3.8) и (3.10) могут быть определены внутренние силовые факторы и исследована прочность конструкции (для многослойной полоски удобнее определять деформации и напряжения в отдельных слоях непосредственно из выражений (3.6) и (3.7)).

Если сечение стержня не изменяется по его длине, то условие (3.19) превращается в линейное дифференциальное уравнение с постоянными коэффициентами, решение которого не составляет труда. Так, например, в случае q = 0 общее решение этого уравнения имеет вид

w(x) = с₁x³ + с₂x² + с₃x + с₄. (3.21)

Для граничных условий (3.20) окончательно получаем

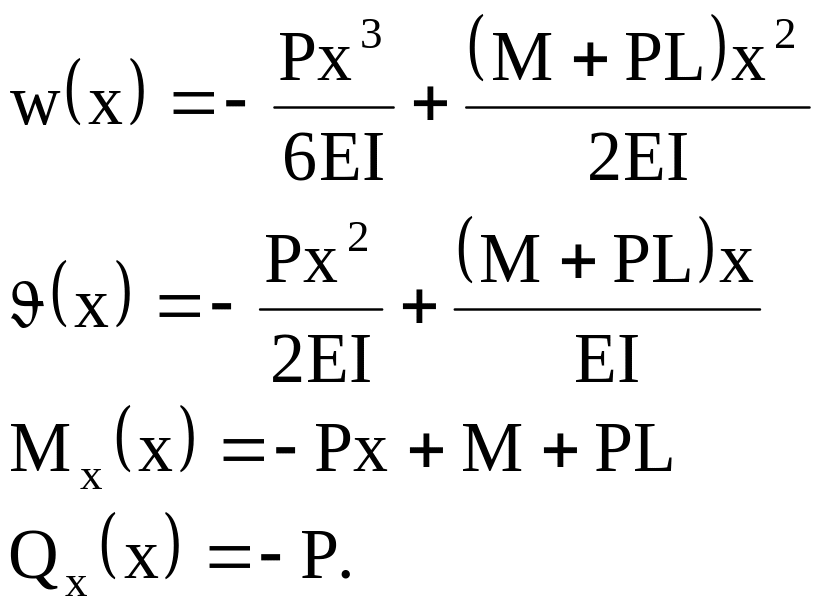(3.22)

В другом важном частном случае, q = const, общее решение

. (3.23)

Для показанного на рис. 3.3,б шарнирно закрепленного стержня, у которого на обоих торцах должны быть равны нулю поперечные перемещения и их вторые производные, решение приобретает вид

(3.24)

Уравнение (3.19) и условия (3.20) могут быть получены и более простым способом, как это делается в курсе сопротивления материалов. Проведя вариационный вывод, мы, однако, получили естественные граничные условия в общем виде. Еще более важно то, что использованная методология может быть применена для вывода разрешающих соотношений в тех случаях, когда необходимо использовать более сложные исходные допущения.

Сделать это придется немедленно. Дело в том, что привычные формулы изгиба балок, полученные на основе гипотезы Бернулли, не всегда могут быть использованы для расчета композитных конструкций. Это связано с внутренним противоречием гипотез Бернулли. Действительно, деформация _xz, как уже отмечалось, полагается равной нулю. Однако соответствующее напряжение _xz равным нулю быть не может, поскольку это означало бы отсутствие перерезывающей силы Q_x, которая связана условием (3.10).

Величины _xz и _xz связаны законом Гука, который для ортотропного тела может быть записан в виде

_xz = G_xz_xz. (3.25)

Сказанное означает, что гипотезы Бернулли могут адекватно описывать изгибное деформирование стержня лишь в том случае, когда его модуль сдвига G_xz бесконечно велик. Разумеется, в практических задачах речь идет не о реальной бесконечности, а лишь о достаточно большой величине этого модуля в сравнении с некой заданной мерой. Как станет ясно позже, эта мера определяется соотношением между величиной G_xz/E_x и отношением поперечных размеров стержня к его длине. Для обычных конструкционных материалов величины модуля упругости и модуля сдвига отличаются множителем 2(1 + ), и использование гипотез Бернулли не приводит к заметным погрешностям в расчетах. Однако для волокнистых композитов эти величины могут различаться на два порядка, так что вопрос о пределах применимости классической теории изгиба встает со всей остротой. Для исследования этой проблемы необходимы более общие подходы. Наиболее простой их них связан с использованием кинематических гипотез Тимошенко.

Гипотезы Тимошенко отличаются от гипотез Бернулли только одним положением: поперечные сечения балки при изгибе остаются плоскими, но не обязательно должны быть перпендикулярны изогнутой оси. Таким образом, угол поворота сечения  не выражается через величину первой производной от прогиба согласно (3.4), а является независимой функцией координаты x. Схема деформирования стержня в этом случае показана на рис. 3.2,б. Разность между функциями (x) и w,_x и составляет тот самый угол сдвига _xz, который теперь может быть связан с напряжением _xz условием (3.25). Итак, основное положение гипотез Тимошенко записывается в виде

 = w,_x + _xz. (3.26)

Остаются справедливыми выражения (3.3) и (3.5) (но не (3.6)!), однако закон Гука включает теперь совместно условия (3.7) и (3.25), а вместо (3.2) должна быть записана более общая формула:

. (3.27)

Для вычисления изгибающего момента и перерезывающей силы вместо (3.8) и (3.10) используются условия

, (3.28)

. (3.29)

В последнем выражении символом GF обозначена сдвиговая жесткость стержня. Величины сдвиговых жесткостей типичных многослойных профилей приведены в таблице 2.1. Расчет характеристик сдвиговой жесткости тонкостенных профилей имеет свои особенности, о которых речь пойдет ниже.

С учетом изложенного, величина потенциальной энергии деформации тела определяется по формуле

. (3.30)

Поскольку условие (3.14) остается в силе, вместо (3.15) следует записать

. (3.31)

Если на балку действуют сосредоточенные силы и моменты, в выражение (3.31) войдут также внеинтегральные слагаемые.

Вариационное уравнение Лагранжа

(3.32)

после интегрирования по частям принимает вид

(3.33)

Дифференциальные уравнения изгиба стержня вытекают из произвольности вариаций  и w в условии (3.33):

(3.34)

Естественные граничные условия при x = 0 и x = L также следуют из условия (3.33):

1. Либо EI,_x = 0, либо  = 0 (последнее условие означает, что задана величина угла поворота сечения ; например,  = 0).

2. Либо GF( – w,_x) = 0, либо w = 0 (последнее условие означает, что задана величина w; например, w = 0).

С учетом (3.28) и (3.29) эти граничные условия могут быть сформулированы для внутренних силовых факторов M_x и Q_x:

1. Либо M_x = 0, либо задана величина .

2. Либо Q_x = 0, либо задана величина w.

Если к торцам стержня приложены сосредоточенные нагрузки, они войдут в граничные условия. Так, например, для рассмотренного выше консольно закрепленного на левом конце и нагруженного силой P и моментом M на правом стержня граничные условия имеют вид

w|_x = 0 = 0

|_x = 0 = 0

[EI,_x – M]_x = L = 0 (3.35)

[GF( – w,_x) + P]_x = L = 0.

Следует обратить особое внимание на второе из условий (3.35): вместо привычной формулы w,_x = 0 в заделке следует использовать условие  = 0. К сожалению, ошибочное использование условий (3.20) вместо (3.35) встречается иногда даже на страницах солидных изданий.

Дальнейшее решение проводится в зависимости от вида функции q(x) в конкретных задачах. После нахождения зависимостей w(x) и (x) определяются все факторы напряженно-деформированного состояния изгибаемого стержня.

Если сечение стержня неизменно по его длине, система уравнений (3.34) может быть преобразована к виду

(3.36)

Для случая q = const общее решение этих уравнений имеет вид

(3.37)

Четыре константы c₁c₄ находятся из четырех граничных условий на торцах стержня.

Для статически определимых задач решение упрощается. В этих случаях можно традиционным методом определить зависимости M_x(x) и Q_x(x), а затем использовать формулы (3.28) и (3.29) для вычисления w и :

(3.38)

В сложных случаях интегралы (3.38) можно брать численно.

В качестве примера рассмотрим известную из курса сопротивления материалов задачу об изгибе консольной балки сосредоточенной силой, приложенной на свободном торце, как это показано на рис. 3.4,а. Уравнения равновесия отсеченной части

Q_x = –P

M_x = P(L – x). (3.39)

Если характеристики профиля не изменяются по длине стержня, из (3.38) следует

(3.40)

Представляет интерес также зависимость w,_x(x):

. (3.41)

Графики зависимостей (3.40) и (3.41) показаны на рис. 3.4,б-г. Следует обратить внимание на то, что w,_x(0)  0, то есть, касательная к упругой линии в заделке не горизонтальна.

Максимальный прогиб имеет место на свободном торце и равен

. (3.42)

Сопоставление с решением, полученным с использованием гипотез Бернулли (3.22) (показано штриховой линией на рис. 3.4,б), показывает, что учет сдвиговой податливости приводит к увеличению прогиба на величину 3EI/L²GF в сравнении с единицей. Формулы, приведенные в таблице 2.1, показывают, что необходимость учета сдвига определяется величиной отношения E_xh²/GL², где h – характерный размер поперечного сечения, в сравнении с единицей (эта безразмерная величина иногда именуется поправкой Тимошенко). Величина G в последнем соотношении характеризует сдвиговую жесткость материала стержня. Как видно из таблицы 2.1, для всех тонкостенных профилей, кроме многослойной полоски, эта характеристика имеет смысл среднего модуля сдвига в плоскости пакета G_xy (1.18)(1.20).

Для правильного понимания формул расчета сдвиговой жесткости стержней GF следует учесть, что напряжения _xz в любой точке тонкостенного сечения можно представить в виде векторной суммы напряжений, направленных вдоль линии контура сечения и по нормали к нему, причем последняя величина должна быть пренебрежимо мала в силу закона парности касательных напряжений (на свободных поверхностях  = 0).

Например, для тонкостенного трубчатого сечения (вторая строка в таблице 2.1) распределение касательных напряжений, направленных вдоль линии контура сечения, иллюстрирует рисунок 3.5:

, (3.43)

где символы ₀ и ₀ обозначают максимальные напряжения в сечении, причем для определения ₀ можно использовать условие

. (3.44)

С учетом (3.29) и (3.26) получается формула для расчета изгибной жесткости GF, приведенная во второй строке таблицы 2.1.

Аналогично, для любого тонкостенного сечения, кроме полоски, величина сдвиговой жесткости может быть записана в виде

GF = kG_xyS, (3.45)

где S – площадь сечения, G_xy – модуль сдвига многослойного пакета, а коэффициент k определяется в зависимости от формы сечения. Для тонкостенной трубки, как показано выше, k = ½, для прочих сечений величина k может быть определена с учетом распределения касательных напряжений по формуле Журавского [14]. При необходимости формула Журавского для полоски может быть уточнена с учетом неоднородности материала в сечении:

, (3.46)

где

. (3.47)

Величина z₀ в последней формуле определяется согласно (2.4).

Сдвиговая жесткость многослойной полоски определяется не модулем сдвига G_xy, а величиной G_xz, определяемой с учетом межслойного сдвига. В первом приближении можно принимать значение G_xz равным модулю сдвига однонаправленного материала G₁₃  G₁₂ (весьма малая величина). Для более точных расчетов можно использовать формулу (3.46).

Итак, возвращаясь к оценке области применимости гипотез Бернулли, следует констатировать, что эта область определяется малостью поправки Тимошенко в сравнении с единицей. Это может быть справедливо в двух случаях:

• либо модуль сдвига композитной структуры достаточно велик (например, если многослойный профиль содержит значительную долю перекрестно армированных слоев);

• либо длина стержня весьма велика.

Если есть сомнения в выполнении указанных условий, следует использовать для расчета стержней формулы (3.26)(3.38).

Необходимо отметить, что гипотезы Тимошенко также не свободны от внутренних противоречий. Так, очевидно, что для сплошного сечения деформация _xz не может быть постоянной по площади сечения, поскольку в крайних точках касательные напряжения должны быть равны нулю в силу закона парности, и, следовательно, условие (3.25) не может быть выполнено. Это делает бессмысленным слишком глубокие уточнения формул для расчета сдвиговой жесткости с использованием (3.46). Вместе с тем, в целом расчетная методика, опирающаяся на соотношения (3.26)(3.38) вполне может быть рекомендована для проектных расчетов, поскольку речь идет лишь о поправке к классическому решению, и эта поправка может быть вычислена с достаточной для инженерных расчетов точностью.

Не менее важно помнить об еще одном допущении, которое также ограничивает точность расчетов многослойных композитных стержней. Дело в том, что при изгибе многослойной полоски напряженное состояние считается одноосным, а закон Гука в каждом элементарном объеме стержня принимается в виде (3.7) с возможной добавкой (3.25). Таким образом, не учитывается наличие поперечных и сдвиговых напряжений в слоях _y⁽ⁱ⁾ и _xy⁽ⁱ⁾, вызванных различием коэффициентов Пуассона материалов и неортотропностью отдельных слоев. Фактически это означает, что в поперечном направлении не выполняется условие совместности деформаций _y: каждый слой в поперечном направлении деформируется свободно в соответствии со своим коэффициентом Пуассона, как если бы имело место проскальзывание по границам слоев (отметим еще раз, что речь идет только о поперечных деформациях). Учет неоднородности поперечных деформаций по толщине полоски приведет к постановке двумерной задачи изгиба пластины и сделает практически невозможным получение аналитических решений.

Стоит заметить, что указанный эффект проявляется только в композитных полосках, для которых коэффициенты Пуассона отдельных слоев могут различаться на два порядка и более [2]. При проектировании стержневых конструкций из традиционных материалов, даже в случае биметаллических полосок, коэффициенты Пуассона слоев были достаточно близкими, чтобы пренебречь поперечным деформированием. Для многослойных композитных полосок это может оказаться несправедливым.

Для прочих многослойных профилей, показанных в таблице 2.1, расчет характеристик изгибной и сдвиговой жесткости ведется с учетом двухосного напряженного состояния слоев, и приведенные в означенной таблице формулы имеют достаточную точность.