Основные объекты проектирования Композитные стержни

Используемые в современной технике композитные стержни обычно можно отнести к одному из двух основных типов:

стержни из однонаправленного волокнистого материала, армированные в продольном направлении;
многослойные тонкостенные стержни;

Однонаправленные стержни, как правило, изготавливаются методом пултрузии. Они могут иметь практически любую форму поперечного сечения. Свойства материала таких стержней одинаковы в любой точке поперечного сечения. Их характеристики могут быть определены по обычным формулам из курса сопротивления материалов, в которые следует подставлять модуль упругости однонаправленного материала в направлении армирования E₁ и модуль сдвига G₁₂.

Многослойные тонкостенные стержни могут быть изготовлены методами намотки на оправку однонаправленной ленты или жгута, а также выкладкой однонаправленных слоев с последующим формованием. Во всех случаях структура многослойного пакета по периметру сечения остается неизменной.

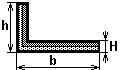
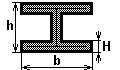
Основные виды многослойных тонкостенных стержней и используемые при их расчетах системы координат показаны на рис. 2.2. Это:

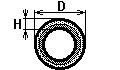
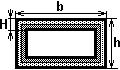
тонкостенные замкнутые профили,
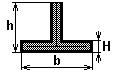
тонкостенные открытые профили,
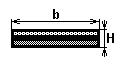
тонкостенная полоска.

Некоторые типы тонкостенных многослойных профилей показаны на рис. 2.3. При расчете характеристик таких стержней обычно можно использовать осредненные свойства многослойного материала. Единственным исключением является изображенная на рис. 2.3,а композитная полоска, при расчете изгиба которой необходимо учитывать не только мембранные характеристики многослойного пакета, но и порядок чередования его слоев.

Основные характеристики, необходимые для расчета стержней:

продольная жесткость EF,
погонная масса m₀,
крутильная жесткость GI_p,
изгибная жесткость EI,
сдвиговая жесткость GF.

Смысл каждой из этих характеристик будет разъяснен при анализе задач статики, устойчивости и динамики стержней. Здесь отметим лишь, что величины EF и m₀ для всех профилей определяются произведением площади сечения F соответственно на средний модуль упругости E_x и среднюю плотность материала  [2].

Крутильная жесткость, строго говоря, определяется только для тонкостенной трубки (рис. 2.3,б):

, (2.2)

где G_xy – средний модуль сдвига многослойного пакета [2], D и H – диаметр и толщина стенки трубки.

Для профилей замкнутого сечения вместо GI_p может быть приближенно определена величина GI_к. Так, например, для тонкостенного прямоугольника (рис. 2.3,в):

. (2.3)

Обозначения в последней формуле поясняются в таблице 2.1.

Для тонкостенных профилей открытого профиля крутильная жесткость не может быть определена по столь простым формулам, так как при их кручении заметное влияние оказывает депланация поперечного сечения [9].

Расчетные формулы для изгибной и сдвиговой жесткости основных типов профилей приводятся в таблице 2.1. Среди этих формул требуют пояснения зависимости для многослойной полоски.

В этих формулах величина E_x⁽ⁱ⁾ есть модуль упругости i-го слоя в направлении оси x полоски, определяемый по первой из формул (1.20) (для неотротропного пакета (1.18)), в которую вместо коэффициентов матрицы жесткости пакета g_xx, g_xy и g_yy следует подставить соответствующие коэффициенты для i-го слоя g_xx⁽ⁱ⁾, g_xy⁽ⁱ⁾, g_yy⁽ⁱ⁾ [2], z_i и z_i_–1 – координаты нижней и верхней границ i-го слоя.

Начало отсчета координаты z определяется условием

^, (2.4)

в котором координата отсчитывается от любой поверхности (например, внутренней или внешней).

Следует учитывать, что при проектировочных расчетах композитных стержней часто бывает недостаточно использовать только стержневые расчетные модели.

Во многих случаях приходится также рассматривать трубчатый стержень как цилиндрическую оболочку, а элементы стержней других профилей – как удлиненные пластины, закрепленные различным образом в зависимости от типа профиля.

Таблица 2.1.

Изгибные и сдвиговые жесткостные характеристики многослойных композитных профилей