3.2. Особенности расчетов на прочность
Как правило, после определения напряженно-деформированного состояния конструкции следует расчет ее на прочность.
Алгоритмы прочностных расчетов многослойных композитных структур подробно изложены в начале данного курса [2]. Не повторяя высказанных там положений, отметим главное: само понятие о прочности композита и тип прочностного расчета зависят от требований, предъявляемых к композитной конструкции в каждом расчетном случае. Двумя основными подходами к расчету прочности композитов являются:
расчет по первому разрушению, когда недопустимы любые необратимые изменения свойств материалов слоев (линейный алгоритм расчета прочности);
расчет предельной несущей способности, когда многослойный пакет перестает воспринимать возрастающую нагрузку (нелинейный алгоритм расчета прочности).
В пособии [2] подробно изложены оба этих алгоритма для случая, когда деформации многослойного пакета постоянны по его толщине. В этом случае исходными данными для расчета являются начальные значения средних напряжений x, y, xy, которые изменяются пропорционально одному параметру нагрузки P:
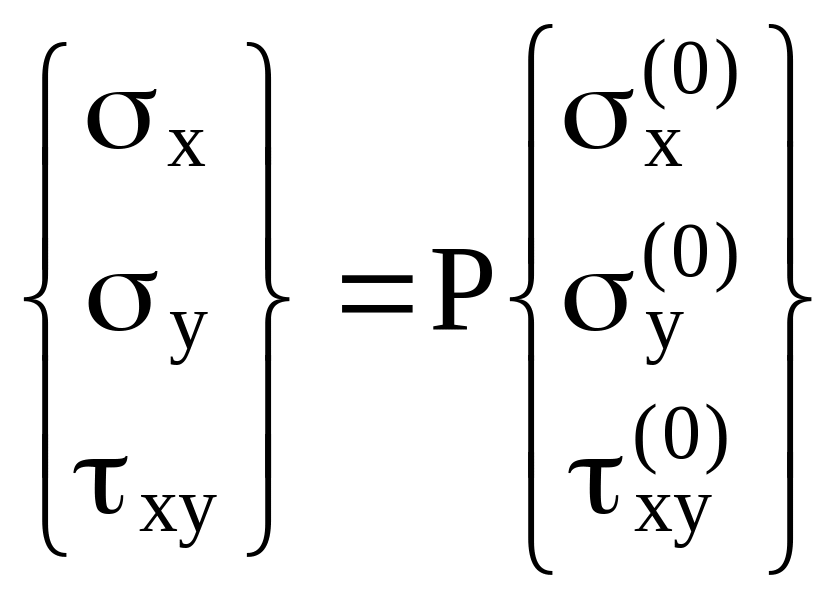. (3.157)
Смысл
расчета заключается в том, чтобы найти
предельное значение P,
показывающее, во сколько раз следует
увеличить заданные напряжения
для достижения предельного состояния
(то есть, величину запаса прочности при
действующих нагрузках).
Ниже рассматриваются дополнительные вопросы, связанные с расчетом на прочность композитных конструкций: анализ прочности при наличии температурной нагрузки и расчет прочности при переменных деформациях по толщине композитной структуры.
3.2.1. Прочность при термосиловых нагрузках
В некоторых расчетных случаях действие внешних силовых факторов, вызывающих напряжения (3.157), дополняется воздействием изменения температуры Т.
Действие температурных нагрузок на композит проявляется двояко. С одной стороны, все характеристики материалов слоев являются функциями температуры (в общем можно считать, что с увеличением температуры и жесткостные, и прочностные характеристики композитов снижаются, хотя и в разной степени – подробнее эти вопросы освещены в [22, 23]). С другой – при изменении температуры многослойного пакета, слои которого характеризуются разными коэффициентами линейного расширения в глобальной системе координат, в этих слоях возникают дополнительные температурные напряжения, влияющие на прочность.
Расчет на прочность при этом зависит от порядка действия силовых и температурных нагрузок и условий закрепления элемента конструкции. Ниже рассмотрен наиболее типичный случай, когда закрепление допускает свободное температурное расширение элемента, а изменение температуры предшествует воздействию силовых факторов.
В
этом случае при изменении температуры
многослойного пакета в нем возникает
самоуравновешенная система температурных
напряжений
,
а при действии силовых факторов эти
напряжения добавляются к напряжениям,
пропорциональным параметру нагрузки:
(3.158)
где i – номер текущего слоя.
Таким образом, линейный алгоритм расчета прочности при термосиловых нагрузках, прежде всего, предполагает расчет термических деформаций в осях конструкции
(3.159)
а затем в естественной системе координат каждого слоя
(3.160)
где i – угол ориентации i-го слоя (для частей слоя, ориентированных под углами +i и –i термические деформации различаются знаком), после чего вычисляются термические напряжения
(3.161)
Коэффициенты линейного термического расширения пакета x и y, коэффициенты термических напряжений слоев 1(i), 2(i) и коэффициенты матриц жесткости слоев g11(i), g12(i), g22(i), g66(i) определяются согласно [2].
Если температурные напряжения меньше соответствующих пределов прочности, то разрушение материала произойдет от внешних силовых факторов, даже если знаки напряжений от этих факторов противоположны знакам температурных напряжений. Таким образом, согласно (3.158) учет температурных напряжений фактически сводится к изменению пределов прочности материалов слоев на величины этих напряжений.
Итак, в линейном алгоритме расчета прочности [2] следует изменить одну последнюю операцию: использование критерия прочности для монослоя, который теперь имеет вид:
, (3.162)
где
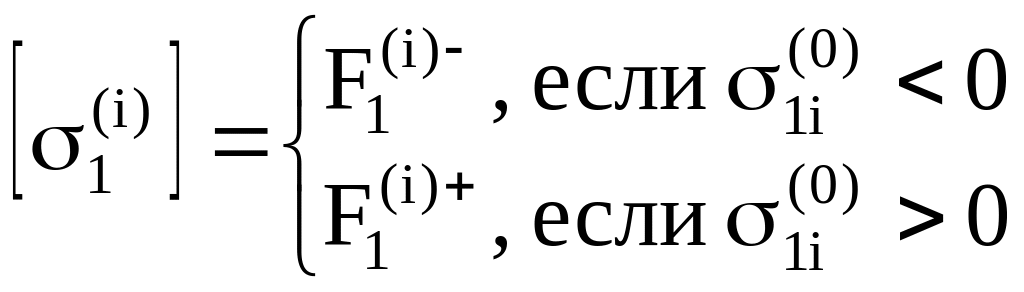(3.163)
В последние выражения пределы прочности подставляются со своими знаками (пределы прочности при сжатии отрицательны). Таким образом, если температурные напряжения и начальные напряжения в слоях имеют один знак – абсолютная величина предела прочности уменьшается, если знаки разные – увеличивается. Что касается сдвига, то в одной части слоя i температурные и начальные напряжения всегда складываются, а в другой – вычитаются; расчет, естественно, ведется по худшему случаю.
Если расчет прочности ведется с использованием нелинейного алгоритма [2], то температурные напряжения вводятся в этот алгоритм как начальные напряжения в слоях.