Основные понятия и задачи механики деформируемого твердого тела

Перед началом изложения расчетных алгоритмов стоит напомнить некоторые понятия, известные вам по курсам сопротивления материалов и механики композитных сред.

Как известно, механика деформируемого твердого тела описывает поведение тел при внешнем воздействии на них (силовом, тепловом воздействии или ином изменении свойств окружающей среды)

При этом она опирается на две основные гипотезы [5, 12]:

• гипотеза сплошности, позволяющая ввести понятие напряженно-деформированного состояния и использовать математический аппарат бесконечно малых;

• гипотеза идеальной упругости, предполагающая, что тело после снятия нагрузок полностью восстанавливает исходное состояние.

В общем виде объект исследования – механическая система – может быть представлен на рис. 1.1. Она включает упругое тело, закрепленное в пространстве при помощи системы жестких или упругих связей и нагруженное системой распределенных и сосредоточенных нагрузок. Объект рассматривается в неподвижной декартовой системе координат xyz, оси которой в дальнейшем будем называть осями конструкции (в отличие от осей материала, которые будут рассмотрены ниже).

Внешние силы подразделяются на объемные, непрерывно распределенные по объему тела, и поверхностные, которые распределены по поверхности границы тела. Частным случаем последних являются сосредоточенные нагрузки. Объемные нагрузки задаются функциями X(x,y,z), Y(x,y,z) и Z(x,y,z), которые описывают силы, действующие в направлении соответствующих координатных осей, поверхностные – соответствующими функциями p_x(x,y,z), p_y(x,y,z) и p_z(x,y,z).

Напряжением (или полным напряжением) в точке называется векторная величина (x,y,z), равная отношению элементарной внутренней силы dF к элементарной площадке dS. Полное напряжение принято раскладывать на касательное  и нормальное _n, спроецировав вектор на плоскость площадки и нормаль к ней. Выделив три площадки, проходящие через исследуемую точку перпендикулярно осям координат конструкции, записывают тензор напряжений

, (1.2)

в котором по закону парности

. (1.3)

В результате внешнего воздействия система занимает некоторое положение равновесия, отличное от исходного недеформированного состояния. Это положение равновесия характеризуется полем перемещений, которое описывается тремя функциями u(x,y,z), v(x,y,z), и w(x,y,z), представляющими собой проекции полного перемещения каждой точки тела на оси координат конструкции.

Полю перемещений соответствует поле деформаций (линейных, представляющих собой относительное изменение длины элементарного отрезка в направлении той или иной оси координат, и угловых, которые равны изменениям исходных прямых углов между этими отрезками).

Как и для напряжений, записывают тензор деформаций

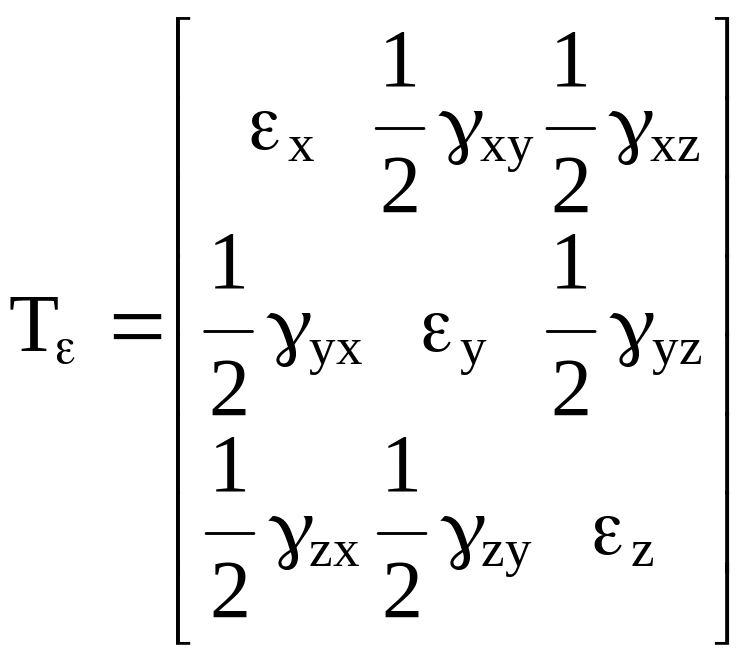, (1.4)

в котором по закону парности

. (1.5)

Деформации однозначно определяются функциями перемещений [12]:

(1.6)

(индексом после запятой здесь и далее обозначается дифференцирование по соответствующей координате, как это принято в вариационном исчислении). В большинстве случаев при расчетах малых деформаций вместо (1.6) используются более простые формулы, устанавливающие линейную связь между деформациями и производными от перемещений:

(1.7)

Уравнения равновесия элемента тела

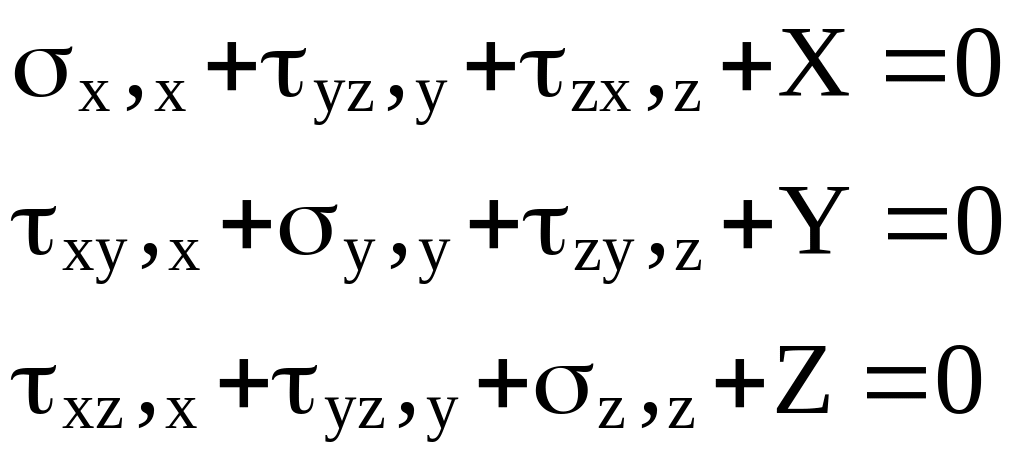(1.8)

дополняются граничными условиями: силовыми

(1.9)

(где l, m, n суть направляющие косинусы нормали к поверхности тела) и геометрическими, которые накладываются на функции u, v, w и их первые производные по координатам x, y, z.

Удельная потенциальная энергия деформации упругого тела U₀ вводится соотношениями

. (1.10)

Для линейно упругого тела независимо от вида его анизотропии справедливо

. (1.11)

В большинстве практических расчетов нет необходимости рассматривать трехмерное напряженное состояние. Так возникает плоская задача. В теории упругости принято различать плоское напряженное и плоское деформированное состояние, однако независимо от того, равны ли нулю три компоненты тензора напряжений или деформаций, в обоих случаях справедливо

, (1.12)

что позволяет не различать эти два состояния в прикладных расчетах элементов конструкций в виде стержней, пластин и оболочек.

Связь между деформациями и напряжениями в линейно упругом теле может быть записана в виде закона Гука. В общем случае анизотропии упругого тела соотношения закона Гука содержат 21 независимую упругую константу [3, 4]. Нас будет интересовать формулировка закона Гука для плоской задачи:

, (1.13)

или, в развернутом виде

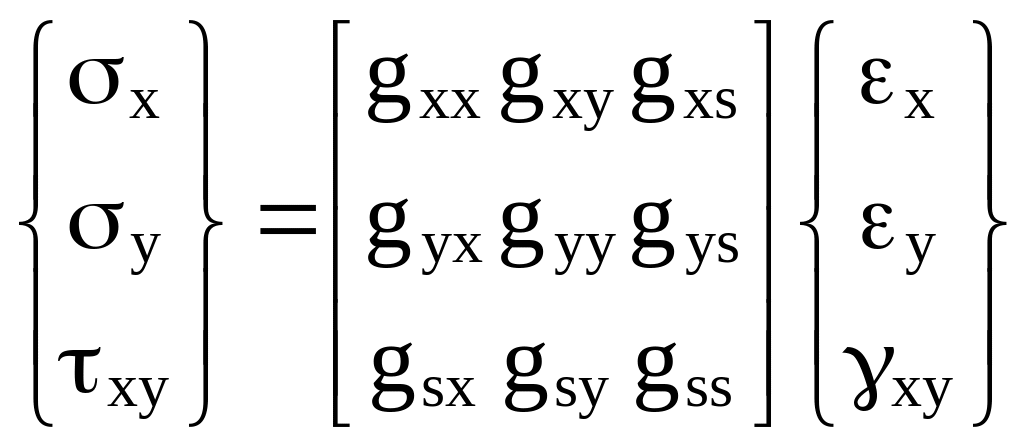. (1.14)

Симметричная матрица жесткости [G_xy] в плоской задаче содержит шесть независимых упругих констант (g_xy = g_yx, g_xs = g_sx, g_sy = g_ys). Для наиболее распространенного случая материала, ортотропного в осях конструкции, g_xs = g_ys = 0, и остается четыре независимые константы (для изотропного материала, напомним, таких констант две)

Соотношения, обратные (1.13), записываются с использованием матрицы податливости [S_xy]:

, (1.15)

где

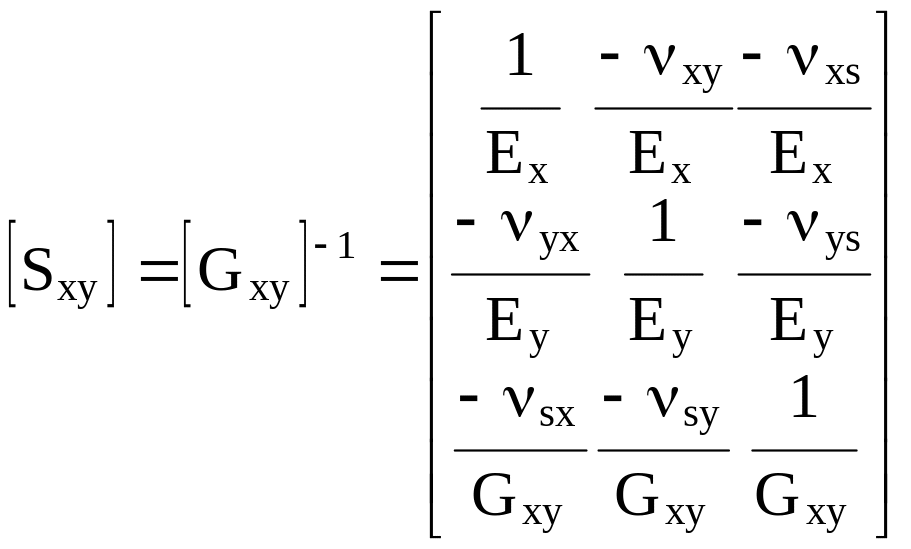, (1.16)

_xyE_y = _yxE_x, _xsG_xy = _sxE_x, _ysG_xy = _syE_y. (1.17)

Таким образом, свойства материала в плоской задаче определяются шестью техническими константами упругости: модулями упругости E_x, E_y, модулем сдвига G_xy и коэффициентами поперечных и сдвиговых деформаций (коэффициенты Пуассона _xy, _xs, _ys; две последних величины представляют собой отношения сдвиговых деформаций _xy, возникающих при одноосном растяжении вдоль осей x и y соответственно, к величинам линейных деформаций вдоль этих осей _x и _y).

Для ортотропного материала число технических констант снижается до четырех (E_x, E_y, G_xy и _xy).

Связь между коэффициентами матрицы жесткости и техническими константами упругости записывается в виде [3, 4]

^(1.18)

или

^(1.19)

Для ортотропного материала

(1.20)

или

^(1.21)

Закон Гука позволяет записать выражение для удельной энергии (1.12) в виде

. (1.22)

Если наряду с силовыми на тело действуют также температурные нагрузки, связь между напряжениями, деформациями и изменением температуры в плоской задаче описывается соотношениями Дюамеля-Неймана [4]

, (1.23)

или

, (1.24)

где Т – изменение температуры в данной точке тела (предполагается, что величина Т достаточно мала, чтобы пренебречь температурными зависимостями свойств материала; в противном случае температурную нагрузку следует разбить на несколько малых шагов). Матрицы [S_xy] и [G_xy] принимаются согласно (1.16), (1.14), а компоненты векторов коэффициентов линейного термического расширения (КЛТР) {_xy} = {_x, _y, _xy}^T и коэффициентов термических напряжений {_xy} = {_x, _y, _xy}^T связаны соотношениями

(1.25)

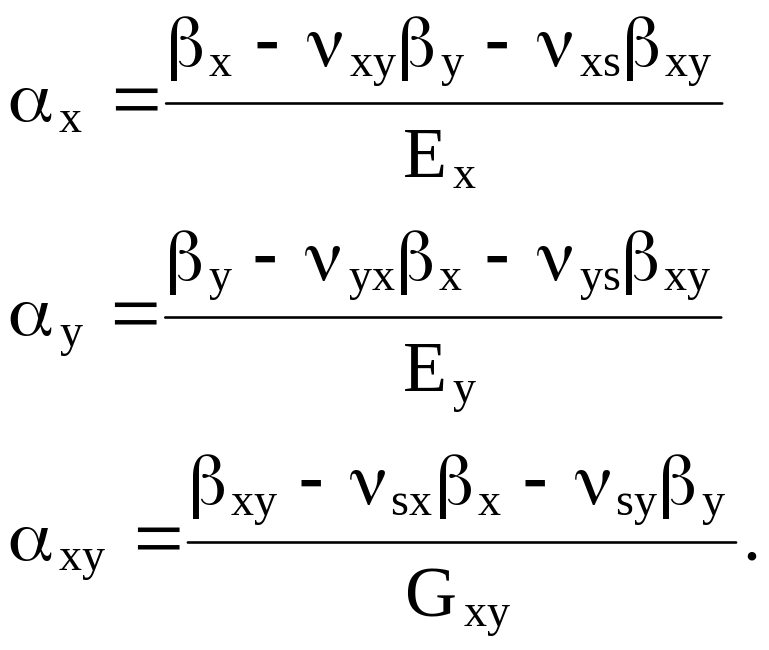(1.26)

Алгоритмы расчета компонент матриц жесткости и податливости, а также векторов КЛТР и КТН многослойного ортотропного материала изложены в [2]; для анизотропного материала общего вида соответствующие формулы приведены в [4].

При расчете удельной потенциальной энергии деформации в плоской задаче с термосиловыми нагрузками следует использовать выражение

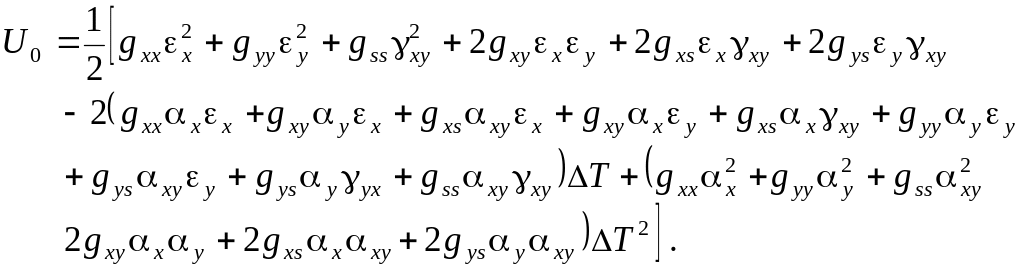(1.27)

Для ортотропного тела величины g_xs, g_ys и _xy в выражении (1.27) следует положить равными нулю.

Задачи механики твердого деформируемого тела подразделяются следующим образом.

1. Задачи статики, предметом которых является исследование равновесных конфигураций механической системы при действующих нагрузках.

В свою очередь, эти задачи можно разбить на две группы:

• расчет напряженно-деформированного состояния тела;

• анализ прочности при действующих нагрузках и определение запасов прочности.

2. Задачи устойчивости, смысл которых состоит в исследовании единственности равновесных конфигураций при действующих нагрузках, определении точек бифуркации и анализе устойчивости выявленных положений равновесия.

3. Задачи динамики, заключающиеся в определении характеристик свободного движения системы вблизи равновесных конфигураций.

Обычно решение этих задач производится разными методами и рассматривается в разных курсах. Однако, поскольку при проектировании конструкций необходим учет свойств, получаемых при решении всех трех групп задач, в данном курсе целесообразно использовать единый инструмент для их решения. Такой универсальный инструмент предоставляет использование принципа минимума полной потенциальной энергии.