29. Применение ортогональных фильтров для статистической идентификации сау.

Один из подходов к статической идентификации линейных САУ основан на разложении весовой функции R(t) в ряд вида:

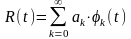(1)

По некоторой системе функций

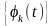
В практических приложениях ряда (1) используется конечное число коэффициентов m разложения .

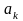Применив в (1) преобразование Лапласа, получим:

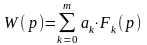(2), где - преобразование по Лапласу

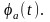
Выражение (2), записанное в частной области, обращается в уравнение:

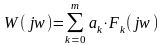(3)

Модель САУ в виде (3) при конечном числе членов разложения и схеме формирования представлена на рисунке:

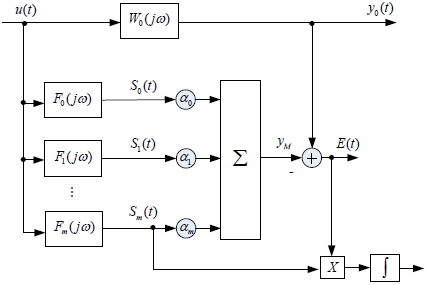
Задачей статической идентификации становится корректной, если в качестве входного воздействия используется сигнал с равномерной спектральной плотностью мощности в полосе частот, превышающей эквивалентную полосу пропускания системы.

Коэффициенты 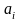определим из условия минимизации интегральной оценки средневзвешенного квадрата погрешности аппроксимации

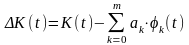
Средневзвешенный квадрат погрешности аппроксимации

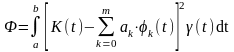
Из условия минимума Ф

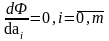
Получаем уравнение:

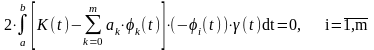
Или

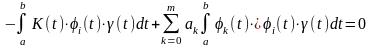
Выберем ортогональную систему функций систему функций, учитывая свойства ортогональности:

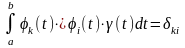
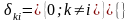
Получим:

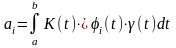(4)

То есть коэффициенты взаимно линейно независимы. Однако формула (4) не позволяет их определить, так как не известна K(t).

23. Построение диагностической модели чувствительности. Методы понижения порядка передаточной функции. Аналитическая и алгоритмическая модели чувствительности в методе поиска одиночных дефектов с использованием интегральных преобразований сигналов.

Диагностической моделью чувствительности назовем упрощенную модель чувствительности объекта диагностирования, используемую для вычисления диагностических признаков и эквивалентную полной модели чувствительности в отношении значений этих признаков. Рассмотрим принцип построения диагностической модели чувствительности на примере алгоритма поиска одиночных структурных дефектов с использованием интегральных преобразований сигналов. Для структурных дефектов условие эквивалентности двух дефектов записывается:

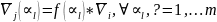
где

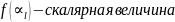
Условие (1) позволяет сокращать векторы структурной чувствительности на общие множители их элементов. Анализ выражения:

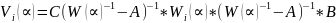
Показывает, что таким общим множителем для всех элементов вектора структурной чувствительности(для всех контрольных точек ОД) является величина

Которая представляет собой оценку ПФ первой модели (до перемычки) структурной модели чувствительности относительно выхода i-го ДЭ, умноженной на величину 1/W2(∝). После сокращения получим эквивалентный в смысле результатов поиска одиночных структурных дефектов вектор структурной чувствительности i-го динамического элемента

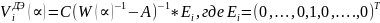-вектор-столбец с единственным ненулевым элементом в i-й строке.

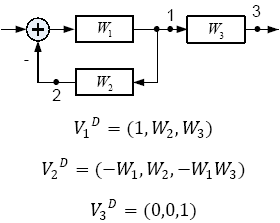
Структурные чувствительности 𝑽𝒊 ДЭ ∝ представляют собой оценки передаточных функций объекта от входа i-го ДЭ до рассматриваемых выходов.

Диагностическая модель чувствительности структурных дефектов предоставляет собой передачи от выхода рассматриваемого блока до соответствующих контрольных точек.

Рассмотрим векторы диагностических моделей чувствительности:

А) Последовательное соединение Параллельное соединение

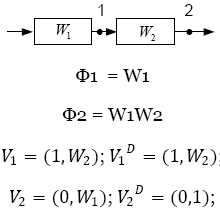
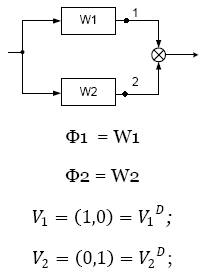
Б) Встречно-параллельное соединение:

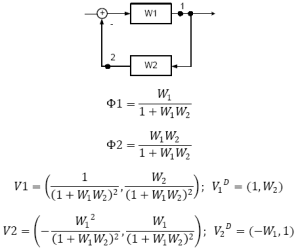
ДМЧ таким образом получается как определение передач от выхода рассматриваемого блока до соответствующей контрольной точки.

Передача от выхода рассматриваемого звена до КТ: