1. Техническая диагностика. Основные термины и определения.

Техн. диагностика – наука о распознавании состояния техн. системы.

Идентификация - это опред. динамической модели на основе измерения входных и выходных сигналов. В широком смысле, идентиф. (структурная) – опред. структуры модели (формула, её вид, порядок модели). В узком смысле, идентиф. (параметрическая) – опред. численных значений коэффициентов.

Е сли система удовлетворяет предъявляемым к ней требованиям по точности функционирования и выходным сигналам, то она называется работоспособной, а, следовательно, нет необходимости искать дефект. Задача идентиф. в любом случае решается с погрешностью. Методы идентиф. могут быть использованы для диагностики (для поиска неисправностей).

Диагностирование – процесс опред. техн. состояния объекта с заданной точностью. Опред. исправности, работоспособности, правильности функционирования. Диагност. предполагает использование динамических режимов, а некоторые задачи решаются только в динамическом режиме, т.к. для диагност. и идентиф. он более информативен.

Диагност. признак (параметр) – это признак, который используется в установленном порядке для опред. техн. состояния объекта.

Функциональное (рабочее) диагност. – диагност. объекта в режиме его нормального функционирования.

Тестовое диагност. (более информативно, чем функциональное) – техн. диагност. с использованием специальных тестовых воздействий, напр. единичной ступени.

Система диагност. – совокупность средств диагност. и объекта диагност.

Диагност. модель – формализ. описание объекта диагност., необходимое для решения задач диагност. Она может быть задана в аналитической, табличной, графической, векторной или в любой другой форме, или их совокупности.

Причины применения средств диагност. Основные причины отказа в технике: 1) применение малоизученных физических явлений для создания новых технических устройств; 2) несоблюдение принципа системности и как следствие применение несовершенных и неадекватных расчётных схем; 3) наличие человеческого фактора при разработке и эксплуатации. 25% времени – опред. части, в которой неисправность, 62% - определение детали с неисправностью, 13% - на восстановление детали.

2. Динамические диагностические модели. Задача о градусниках.

Н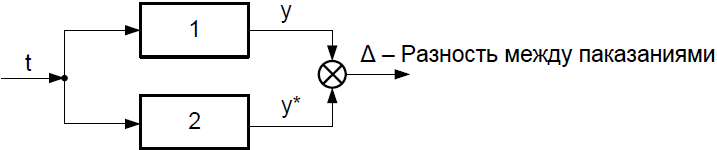 а стене рядом висят 2 градусника. Они показывают разную температуру. Можно ли опр. какой градусник показывает неправильно?

Градусник описывается звеном .

Воспользуемся простейшей моделью термометра (динамической).

Т* = Т + ∆Т.

Разность между показаниями градусников пропорциональна выходному сигналу неисправного градусника, пропущенному через фильтр с известной передаточной функцией .

Рассмотрим дефект К* = К + ∆К.

Поскольку температура x неизвестна, то определить неисправный градусник невозможно.

Поэтому решим эту задачу в динамическом режиме.

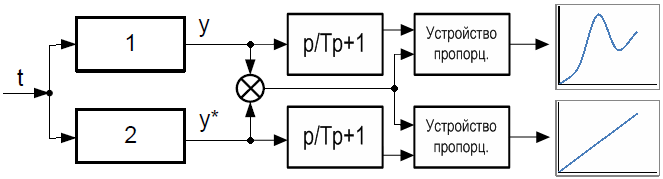
3. Диагностирование двух идентичных каналов в динамическом режиме.

Запишем уравнения градусников в следующем виде:

1 в знаменателя нужна для однозначности задания модели.

Нарушение условия n ≥ m – нарушение дифференцирования, физической реализуемости, т.е. не может быть такого, что на выходе сигнал будет раньше, чем на входе.

О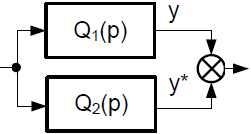 пределим неисправный канал, когда меняется 1 параметр: параметр числителя или знаменателя.

- модель неисправного знаменателя.

- модель неисправного числителя.

1)

- выходной сигнал неисправного канала.

Разностный сигнал ∆ пропорционален выходному сигналу неисправного (второго) блока, пропущенного через фильтр с известной передаточной функцией , причём величина отклонения ∆a_i оприделяется как коэффициент пропорциональности между сигналами ∆ и выходными сигналом фильтра.

2) Аналогично, если одиночный дефект в числителе, можно показать:

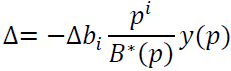
- выходной сигнал исправного канала.

Разностный сигнал ∆ пропорционален выходному сигналу исправного блока, пропущенного через фильтр с известной передаточной функцией .

В обоих случаях фильтры реализуемы.

4. Классификация методов диагностирования.

1. По виду мат. моделей объекта диагностирования

1.1. Модели во временной и частотной области

1.2. Статические и динамические

1.3. Детерминированные и вероятностные

2. По режиму диагностирования

2.1. Функциональное (рабочее)

2.2. Тестовое

3. По моделям дефектов

3.1. Искажения сигналов

3.2. Искажение параметров

4. По характеру диагностических признаков

4.1. В пространстве параметров

4.2. В пространстве сигналов

5. По принципу диагностирования

И 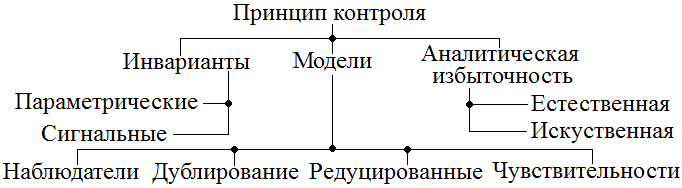нварианты – соотношения, которые остаются постоянными при любых сигналах объекта.

y’’+a₁y’+a₂y=kx

y’’+a₁y’+a₂y-kx=0 – инвариант.

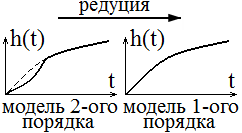
Редуцированная модель – упрощённая.

Редуцировать можно не всегда.

5 . Модели чувствительности (МЧ) систем управления.

МЧ могут строиться во временной или частотной областях.

У (2) шире полоса пропускания, следовательно система (2) более быстродействующая для ФНЧ.

Модель чувствительности временных или частотных характеристик отвечает на вопрос: как влияют параметры системы на временные или частотные характеристики системы. Все выходные сигналы можно обозначить вектором . 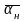- вектор номинальных параметров – включает в себя все коэффициенты усиления постоянной времени.

- функция чувствительности (i-ого параметра).

- матрица чувствительности (высота – количество отсчётов k*n, ширина – количество параметров m).

Относительная функция чувствительности

- логарифмическая функция чувствительности.

Полуотносительная функция чувствительности

- полулогарифмическая функция чувствительности.

Полуотносительная функция чувствительности

- полулогарифмическая функция чувствительности.

(1)

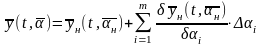(2)

m – общее количество параметров.

(3)

Зафиксируем время с шагом t_j, 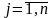и запишем (3) в векторном виде:

(4)

(4) – система линейных алгебраических уравнений. 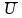размерностью (k × m), где k ≥ m.

(5)

В (5) 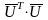- квадратная матрица [m × m]. Заменим ; .

(6)

(6) – нахождение параметрического дефекта произвольной кратности.

Обусловленность матрицы определяется: 1) правильным выбором отсчётов временной или частотной области; 2) от количества контрольных точек и их расположения; 3) от характера входного сигнала.

(7)

(7) – вектора должны быть различимы. Для устранения неразличимости можно: увеличить число контрольных точек (а точнее изменить их положение); изменить входные сигналы во временной области; изменить частотный диапазон в частотной области.

При диагностировании по частотным характеристикам мы будем иметь коэффициенты чувствительности в частотной области.

6. Алгоритм поиска одиночных параметрических дефектов по частотным характеристикам на основе модели чувствительности (МЧ).

Дефектом объекта диагностирования - отклонение прямого показателя диагностической модели от номинального значения на величину, превышающую максимально допустимую.

Одиночным параметрическим дефектом называют такое изменение технического состояния ОД, которое приводит к изменению одного параметра из множества параметров всех передаточных функций ДМ.

Алгоритм:

1. При контроле ОД определяется вектор-функция отклонений амплитудных частотных характеристик (ачх) ОД (или каких-нибудь частотных характеристик):

2. Предварительно определяется матрица чувствительности 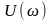размером ачх ОД к изменению прямых показателей , с элементами

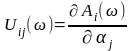, , , – амплитудная частотная характеристика ОД.

3. Вектор отклонений прямых показателей от номинальных значений , по элементам которого выносится диагноз, определяется как решение векторного уравнения

(1), где , – соответственно нижняя и верхняя границы контролируемого диапазона частот; T – символ транспонирования.

Столбцами матрицы являются вектор-функции чувствительности , .

частотные характеристики контролируются для конечного числа n дискретных значений аргумента . В этом случае выражения для матриц C и P примут вид Можно считать, что принимается гипотеза о наличии одиночного параметрического дефекта в объекте. В этом случае матричное уравнение (1) преобразуется в совокупность уравнений, каждое из которых содержит лишь один прямой показатель модели: С11*Δα1=P1; С22*Δα21=P21;… Сm_km_k*Δαm_k=Pm_k. (4)

Из уравнений (4) получим 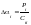, (5). Для вектора остаточной ошибки, применительно к i-му прямому показателю, справедливо выражение 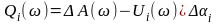. (6) ΔA(ω) – реальная деформация диагностических характеристик, U(ω)Δα_i – модельное деформирование динамических характеристик. Если избавимся в (6) от Δα_i подставив его из (5), (7) подставив (7) в (6) получим:

Учитывая обозначения в выражениях (4) и произведя замену согласно (5), получим . (8)

Переходя от векторов к их элементам, будем иметь

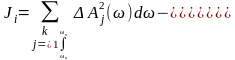, (9)

где k- число контрольных точек в объекте.

Переходя от векторов к их элементам:

(10)

здесь - ненормированный признак, поделим (10) на него:

, где - длина вектора А, - длина вектора Ui.

- скалярное произведение.

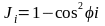φi – угол между 2мя единичными векторами(вектором деформации частотной характеристики и вектором чувствительности).

- диагностический признак одиночного параметрического дефекта, есть квадрат синуса угла между двумя единичными векторами: 1ый – вектор деформации, 2ой – вектор чувствительности. Та параметрическая чувствительность которая минимизирует диагностический признак, котор. имеет наименьший угол с реальной деформацией указывает на дефектный параметр.

7. Алгоритм поиска одиночных параметрических дефектов по временным характеристикам на основе МЧ.

Реализация метода поиска одиночного параметрического дефекта по временным характеристикам предполагает применение следующих теоретических положений и выполнение совокупности действий:

1. В качестве объекта диагностирования рассматривают систему, состоящую из произвольно соединенных m динамических элементов.

2. Предварительно определяют время контроля , где – время переходного процесса объекта. Время переходного процесса оценивают для номинальных значений параметров объекта диагностирования.

3. В режиме тестового диагностирования на вход объекта диагностирования и его эталонную временную модель подают тестовое воздействие (единичное ступенчатое, линейно возрастающее, прямоугольное импульсное и т.д.). Принципиальных ограничений на вид входного тестового воздействия предлагаемый способ не предусматривает. В режиме рабочего диагностирования рабочие входные воздействия объекта диагностирования подают на вход его эталонной временной модели

4. Регистрируют реакцию объекта и эталонной модели в k контрольных точках и определяют отклонения реакций объекта от номинальных , i=1,2,...,k на интервале .

5. В качестве диагностического признака наличия дефекта в i - м динамическом элементе используют интегральную меру вида , где ; – вектор отклонений реакций объекта в k контрольных точках; – вектор параметрической чувствительности (чувствительности реакций объекта в различных контрольных точках к изменению i-го параметра).

При использовании значений сигналов, снятых в дискретные моменты времени с постоянным шагом дискретизации получим формулу для определения нормированного диагностического признака наличия i - го одиночного параметрического дефекта

(1)

Функционал (1) отображает совокупности значений двух дискретных вектор-функций параметрической чувствительности и отклонения реакций объекта диагностирования 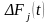на отрезок [0, 1], причем, если выполняется соотношение для k – векторов чувствительности в непрерывном случае или в дискретном случае, где - скалярная константа, то дефекты i и m не различимы.

При использовании нормированного диагностического признака (1) необходимо контролировать величину нормы отклонения реакций ОД от номинальных значений, поскольку при малых ее значений возможны ошибки диагноза, связанные с делением на малое число. В тех случаях, когда значения вектор-функций чувствительности в разных контрольных точках существенно отличаются (на порядок и более) целесообразно использовать относительные функции чувствительности.

8 и 11. Алгоритм поиска одиночных параметрических и структурных дефектов по временным характеристикам с использованием интегральных преобразований сигналов на основе МЧ.

1. Для получения диагностических признаков динамических элементов будем использовать преобразования по Лапласу временных функций в области вещественных значений переменной Лапласа в интервале . Использование преобразования Лапласа при диагностировании позволяет перейти от обработки временных функций к анализу численных значений их функционалов.

2. Будем предполагать, что выполняются достаточные условия существования преобразований Лапласа сигналов ОД 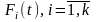: 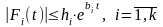, где .

3. Модуль абсолютной погрешности растет с уменьшением параметра 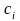, представляющим разность переменной Лапласа и показателя роста 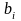сигнала : 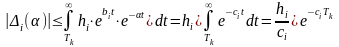, где .

4. Параметр для ограниченных сигналов необходимо выбирать с учетом их области изменения и определения, то есть с учетом площади окна, в котором задан интегрируемый сигнал.

При ограниченных задающих воздействиях на входе устойчивого ОД, можно принять и , тогда .

При задании параметра в величинах, кратных обратным значениям интервала контроля 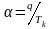, оценка погрешности примет вид . При выборе, например, параметра преобразования Лапласа имеем оценку погрешности .

5. В качестве диагностического признака наличия дефекта в i - м динамическом элементе используют интегральную меру следующего вида: , где ; m – число значений переменной Лапласа, для которых находятся изображения сигналов; – вектор изображений для вещественных значений переменной Лапласа отклонений временных характеристик объекта в k контрольных точках; – структурная чувствительность (чувствительность оценок изображений временных характеристик объекта к изменению передаточной функции i - го динамического элемента); – отклонение передаточной функции i - го динамического элемента от номинального значения.

Для того, чтобы диагностический признак не зависел от неизвестного и искомого на этапе поиска дефектов отклонения , выражаем это отклонение из системы уравнений и, производя преобразования, получаем:

, где 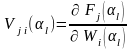– структурная чувствительность изображения временной характеристики в j - ой контрольной точке для i - го динамического элемента и l - го значения переменной Лапласа .

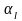6. По минимуму значения диагностического признака выносят решение о наличии дефекта в динамическом элементе.

9. Алгоритм поиска одиночных структурных дефектов по частотным характеристикам на основе МЧ.

Под одиночным структурным дефектом будем понимать такое изменение технического состояния объекта, которое приводит к изменению частотных характеристик только одного динамического элемента. В этом случае задача поиска дефекта заключается в определении номера того динамического элемента (ДЭ), изменение частотной характеристики которого в наибольшей степени изменило бы рассогласование модельных и реально наблюдаемых отклонений частотных характеристик всего объекта.

В качестве меры такого рассогласования, применительно к j-му ДЭ, примем значение функционала вида где – вектор остаточной ошибки для j-го ДЭ; – отклонение частотных (для определенности далее - амплитудных) характеристик всего объекта от номинальных значений; 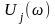– j-й вектор-столбец матрицы чувствительности. При контроле n отсчетов частотной характеристики, использовании k контрольных точек и после нереально крутых преобразований на пару листов, окончательно получим функционал:

где херня, похожая на единицу – это буква L, – отклонение частотной характеристики всего объекта от номинального значения в i-й контрольной точке; – значение функции чувствительности на частоте для i-й контрольной точки и j-го динамического элемента. Неисправным принимается тот ДЭ, которому соответствует наименьшая по модулю величина полученного функционала. => Алгоритм поиска дефектов ДЭ: 1) экспериментально определяются значения амплитудных частотных характеристик диагностируемой системы на фиксирован­ных частотах для каждой контрольной точки; 2) определяют отклонения от номинальных значений АЧХ для каждой контрольной точки и частоты ; 3) используя модель чувствительности объекта диагностирования для каждого динамического элемента, вычисляют значения полученного огромного функционала; 4) неисправным принимается тот динамический элемент, которому соответствует минимальное по модулю значение функционала.

Для анализа контролепригодности САУ полезны следующие утверждения.

Утверждение 1. Если двум динамическим элементам соответствует пара вектор – функций чувствительности такая, что выполняется услови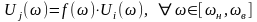е , где 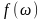- любая скалярная вещественная функция аргумента , то одиночные структурные дефекты динамических элементов с номерами i и j эквивалентны при поиске их с использованием этих функций чувствительности. Далее следует нецензурное доказательство которое мы опустим. Таким образом, при поиске одиночного структурного дефекта требование линейной независимости вектор – функций в диапазоне контролируемых частот для параметрического дефекта заменяется на более строгое требование линейной независимости на каждой частоте контроля.

Утверждение 2. Если два динамических элемента с номерами i и j имеют эквивалентное положение в объекте диагностирования, то при поиске одиночных дефектов по амплитудным частотным характеристикам их структурные дефекты не различимы. Доказательство было замечательное, но его мы тоже опустим

10. Алгоритм поиска одиночных структурных дефектов по временным характеристикам на основе МЧ.

Для уменьшения временных и аппаратных затрат на диагностирование и упрощения процесса диагностирования целесообразно распространить алгоритм поиска одиночных дефектов по частотным характеристикам с использованием модели структурной чувствительности на временную область. В этом случае реализация метода поиска одиночного структурного дефекта по временным характеристикам предполагает применение следующих теоретических положений и выполнение совокупности действий:

1. В качестве объекта диагностирования рассматривают систему, состоящую из произвольно соединенных m динамических элементов.

2. Предварительно определяют время контроля , где – время переходного процесса объекта. Время переходного процесса оценивают для номинальных значений параметров объекта диагностирования.

3. В режиме тестового диагностирования на вход объекта диагностирования и его эталонную временную модель подают тестовое воздействие (единичное ступенчатое, линейно возрастающее, прямоугольное импульсное и т.д.).

4. Регистрируют реакцию объекта и эталонной модели в k контрольных точках и определяют отклонения реакций объекта от номинальных на интервале от 0 до Тк

5. В качестве диагностического признака наличия дефекта в i - м динамическом элементе используют интегральную меру следующего вида: , где ; – вектор отклонений реакций объекта в k контрольных точках; – вектор структурной чувствительности (чувствительности реакций объекта в различных контрольных точках к изменению весовой функции i-го динамического элемента); – интегральное отклонение весовой функции i-го динамического элемента от номинального значения. Чтобы получить искомые чувствительности , необходимо входной тестовый сигнал подать на модель структурной чувствительности с передаточной функцией . Где Ф(p) – передаточная функция всей системы; W_i(p) – передаточная функция i - го динамического элемента. Модель структурной чувствительности может быть получена путем последовательного соединения двух одинаковых моделей объекта, когда выходом первой модели является входной сигнал i - го динамического элемента, а вход второй модели организуется на выходе i - го динамического элемента. 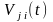Если подать на такое последовательное соединение двух моделей тестовое или рабочее воздействие Х_вх(t), то на выходах контрольных точек второй модели появляются сигналы, численно равные структурным функциям чувствительности i-го блока. Время поиска дефектов может быть снижено за счет дополнительных аппаратных затрат путем одновременной реализации моделей чувствительности для всех динамических элементов. Алгоритм остается работоспособным при одновременном отклонении нескольких параметров в одном динамическом элементе и использовании других видов тестовых воздействий.