Лекции по мат. анализу / Лекция 18

Лекция 18 . Вычисление определенного интеграла.

П.1 Интеграл как функция верхнего предела.

Пусть - непрерывная функция на отрезке . Рассмотрим функцию

, определенную на отрезке . В силу оценки , функция непрерывна на отрезке .

ТЕОРЕМА 1.

Производная интеграла по верхнему пределу равна значению подынтегральной функции.

ДОК. Вычислим производную функции в точке . Для этого представим приращение , где

. Тогда из теоремы о среднем для интеграла и непрерывности функции следует, что 0, где . Таким образом, функция дифференцируема в точке и ее производная равна .

Если или , то обеспечивается правосторонняя или левосторонняя производная

функции .

СЛЕДСТВИЕ. Если функция кусочно – непрерывна на , то имеет производную равную в точках непрерывности, а точках разрыва функция производной не имеет, но остается непрерывной( разрыв производной первого рода)

Следующая теорема связывает понятия первообразной и интеграла Римана.

Пусть - кусочно – непрерывная функция на . Всякая непрерывная на функция называют первообразной функции , если в точках ее непрерывности

. Если и две первообразные , то на каждом интервале непрерывности функции , но в силу непрерывности и константа C сохраняется единой на всех интервалах, т.е. . Согласно теореме 1 функция является первообразной функции даже, если она кусочно- непрерывна.

ТЕОРЕМА 2.( ФОРМУЛА Ньютона-Лейбница)

Если - кусочно – непрерывная функция на и - любая ее первообразная.

Тогда .

ДОК. Функция . Подставляя , получим , т.е.

. Подставляя , получим =.

П.2 Интегрирование по частям в определенном интеграле.

ТЕОРЕМА 3. (ФОРМУЛА интегрирования по частям)

Если - кусочно- гладкие (имеющие кусочно-непрерывную производную) функции на отрезке , то .

ДОК. .

ПРИМЕР 1. Вычислить интеграл .

РЕШЕНИЕ. =

. Тогда .

и для четного .

. Для нечетного

П.3 Замена переменной в определенном интеграле.

Пусть задан интеграл от непрерывной на функции и функция

, определенная на отрезке , имеющая непрерывную производную в каждой точке отрезка и .

ТЕОРЕМА 4.

Если функция :и функция непрерывна на , то справедлива формула : .

ДОК. Пусть первообразная функции на . Тогда формула замены переменной для неопределенного интеграла утверждает, что является первообразной функции на отрезке и , где произвольная первообразная этой функции. Тогда по формуле Ньютона-Лейбница

.

ПРИМЕР 2 . Доказать, что .

РЕШЕНИЕ. Сделаем замену . Тогда .

П.4 Теоремы о среднем для определенного интеграла.

ТЕОРЕМА 5. Пусть функции непрерывны на отрезке и для . Тогда существует точка , для которой .

ДОК. Из непрерывности функции следует, что область ее значений на отрезкеесть отрезок . Тогда с учетом положительности значений функции справедливо неравенство : . После его интегрирования на отрезке : . Тогда величина , т.е. существует , для которого .

При получим знакомый результат : .

ТЕОРЕМА 6. . Пусть функции непрерывна на отрезке , функция непрерывна на и имеет производную во внутренних точках, причем . Тогда существует точка , для которой .

ДОК. Рассмотрим функцию , являющуюся первообразной функции на отрезке , и применим к интегралу формулу интегрирования по частям :

.

Функция непрерывна на , поэтому существуют числа и , для которых значения для . С учетом и , имеем :

или . Тогда существует , для которой .

Если функция неотрицательна и неубывает на отрезке , то справедливо равенство для некоторого .

УПРАЖНЕНИЕ.

1) Докажите, что .

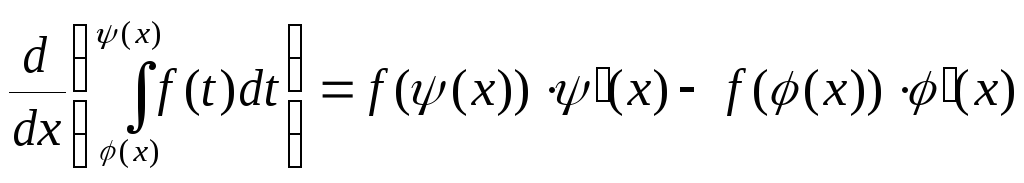2) Докажите, что для периодической функции с периодом T интеграл на отрезке длины периода не зависит от его начала : , .

ВОПРОСЫ К ЭКЗАМЕНУ.

1) Интеграл с переменным верхним пределом. Теорема о дифференцировании интеграла по верхнему пределу

2) Формула Ньютона – Лейбница.

3) Формула интегрирования по частям в определенном интеграле. Пример.

4) Формула замены переменной в определенном интеграле.

5) Теоремы о среднем для определенного интеграла.