Лекции по мат. анализу / Лекция 19

Лекция 19 Приложение определенного интеграла. Площадь, длина кривой.

П.1 ПЛОЩАДЬ КРИВОЛИНЕЙНОЙ ТРАПЕЦИИ.

ОПР. Площадью фигуры Ф называют число , которое не больше, чем площадь объемлющей элементарной фигуры , например, составленных из многоугольников, и не меньше, чем площадь любой объемлемой элементарной фигуры .

Поскольку , следует считать, что площадь имеет та фигура, для которой

.

ОПР. Криволинейной трапецией называют фигуру на плоскости, ограниченную осью ОХ,

прямыми с уравнениями и и кривой графика функции , определенной на отрезке .

Пусть разбиение отрезка . В качестве объемлющей фигуры для криволинейной трапеции выбираем также криволинейную трапецию, построенной для

кусочно-постоянной функции . Аналогично, объемлемой фигурой для криволинейной трапеции будем считать криволинейную трапецию, построенную для кусочно-постоянной функции 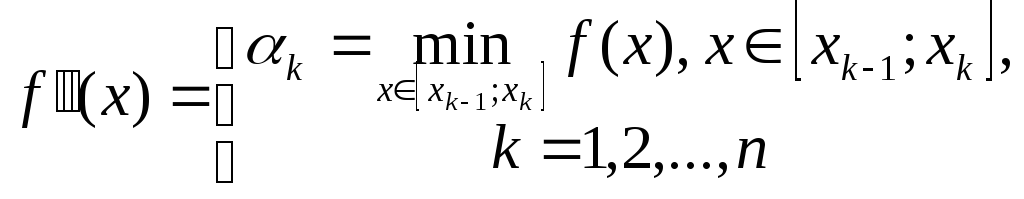. Тогда и .

Выражения для и являются интегральными суммами ( верхняя и нижняя интегральные суммы Дарбу) . Если разбиение , то сумма убывает,

а - возрастает. Если функция интегрируема, то =.

Если на отрезке , то площадь криволинейной трапеции равна -.

Если функция меняет знак на отрезке , то на отрезках , где интеграл берется со знаком +, а на отрезках , где , интеграл берется со знаком - .

ОПР. Элементарной областью на плоскости называют фигуру, ограниченную

прямыми с уравнениями и , графиками непрерывных функций

и ,

ОПР. Элементарной областью на плоскости называют фигуру, ограниченную

прямыми с уравнениями и , графиками непрерывных функций

и , .

ФОРМУЛЫ ВЫЧИСЛЕНИЯ ПЛОЩАДЕЙ фигур и .

и .

ДОК. Если и - криволинейные трапеции , соответствующие функциям и

на отрезке и , то . Тогда .

Если , но на некоторых промежутках, то существует число , для которого для функций и выполняется условие

. Площади элементарных фигур, построенных для функций и на отрезке равны, т.е.

.

Формула для площади фигуры доказывается аналогично. Площадь имеют фигуры, являющиеся конечным объединением элементарных областей типа и .

ПРИМЕР 1. Площадь сектора окружности радиуса r с углом  .

РЕШЕНИЕ.

.

Если граница криволинейной трапеции задается параметрически , ,

- возрастающая функция, , , . Тогда .

Действительно, по доказанному .

П 2. Вычисление площади в полярной системе координат.

ОПР. Элементарной областью на плоскости называют фигуру, ограниченную лучами и , кривой .

ФОРМУЛА ВЫЧИСЛЕНИЯ ПЛОЩАДИ в полярной системе координат.

Если функция непрерывна на отрезке , то площадь области вычисляется по формуле : .

ДОК. Пусть - разбиение отрезка . Пусть и

. Тогда объемлющей фигурой для является элементарная область, ограниченная кусочно-постоянной функцией и лучами

и , имеющая площадь . Объемлемой фигурой для является элементарная область ограниченная кусочно-постоянной функцией и лучами и , имеющая площадь . Числа и являются интегральными суммами функции на отрезке (верхняя и нижняя интегральные суммы Дарбу, см. Пример 1). Если

разбиение , то сумма убывает, возрастает.

Если функция интегрируема на отрезке , то

.

ПРИМЕР 2. Найти площадь одного лепестка кривой ( m – лепестковая роза).

РЕШЕНИЕ. . .

П.2 ДЛИНА ДУГИ КРИВОЙ.

ОПР. Дуга кривой разбивается точками , на n сегментов, концы которых

соединены отрезками .,образующими ломанную линию . Ее длина зависит от дуги кривой и разбиения кривой точками , . Длиной кривой называют число, равное , если оно существует.

Рассмотрим дугу графика функции на отрезке . Каждому разбиению отрезка соответствует ломаная, состоящая из объединения отрезков с началом в точках и концом в точке, .

Длина ломанной равна , где и Если функция имеет непрерывную производную на отрезке , то по теореме Лагранжа существует набор точек , для которых . Тогда длина ломанной является интегральной суммой непрерывной функции и поэтому

=.

ФОРМУЛА ВЫЧИСЛЕНИЯ ДЛИНЫ ДУГИ, заданной параметрически.

Если дуга кривой задана параметрическими уравнениями , , в которых функции имеют непрерывные производные, то

.

Для ее доказательства заметим, что разбиение порождает разбиение дуги кривой точками и длину ломанной , где и .По теореме о среднем для производной существует набор и точек на отрезках , для которых и . Тогда длина ломаной равна

.

Полученное выражение по форме отличается от интегральной суммы функции , поскольку наборы и ,вообще говоря , различные.

Если интегральная сумма функции на отрезке соответствующая разбиению ,то . Для любого

. Вторая часть оценки использует « неравенство треугольника»

.

В предположении непрерывности производных и колебания и - бесконечно малые функции в точке , поэтому существует такое , что для любых . Тогда для разбиений

.

ФОРМУЛА ВЫЧИСЛЕНИЯ ДЛИНЫ ДУГИ, заданной в полярной системе.

Если , - уравнение кривой в полярной системе координат, то

. Тогда и .

Вычислим и получим искомую формулу

.

ПРИМЕР 3. (длина цепной линии)

Вычислить длину дуги, заданной уравнением .

РЕШЕНИЕ. .

УПРАЖНЕНИЕ. Область ограничена графиком непрерывно дифференцируемой функции

и прямой , проходящей через точки и

(сегмент криволинейной трапеции ). Доказать, что ее площадь .

РЕШЕНИЕ. , где . Тогда

, где - функция колебания для производной на отрезке . Из предположения о непрерывности следует, что .

ВОПРОСЫ К ЭКЗАМЕНУ.

1. Доказательство формулы для вычисления площади криволинейной трапеции.

2. Доказательство формулы для вычисления площади фигуры, ограниченной кривой,

заданной параметрически. Вычисление площади фигуры, граница которой задана

уравнением в полярной системе координат.

3. Длина дуги кривой заданной графиком функции, параметрическими уравнениями,

уравнением кривой в полярной системе.