Лекции по мат. анализу / Лекция 26

Лекция 26 . Условный экстремум, наибольшее и наименьшее значение в области.

П.1 Условный экстремум.

ОПР. В точке функция имеет условный максимум

(минимум), если для любых , удовлетворяющих условиям ,., , ().

В отличие от локального экстремума здесь предполагается выполнение неравенства не для всех , а только тех, которые удовлетворяют системе m уравнений

, (связей).

ПРИМЕР 1. Исследовать функцию на экстремум, если переменные x и y связаны соотношением : .

РЕШЕНИЕ. Выражая y через x из уравнения связи и подставляя его в функцию, получим

квадратный трехчлен, имеющий минимум в точке . Тогда функция на прямой имеет условный минимум в точке .

Предположим, что функции и дифференцируемы и система связей определяет неявно функции . Здесь переменные

полагаются свободными, а переменные зависимыми от них. Дифференциалы зависимых переменных равны ,

.и выражаются линейно через дифференциалы свободных переменных. Тогда дифференциал функции связан с дифференциалами свободных переменных соотношением : .

Для вычисления частных производных воспользуемся системой уравнений связи :

тождественны по свободным переменным. Тогда частные производные связаны системой линейных уравнений : 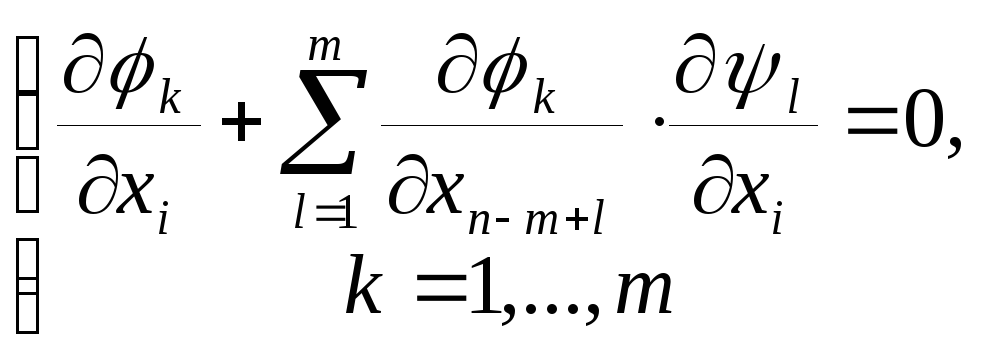. По предположению о ранге системы связи, определитель матрицы порядка mm отличен от нуля и система имеет решение :

. Если обозначить через матрицу строку из частных производных функции по зависимым переменным,

матрицу столбец , , то дифференциал функции имеет вид :. Отсюда вытекают необходимые условия условного экстремума.

ТЕОРЕМА 1. Если функции и дифференцируемы в точке , матрица порядка m n в точке имеет ранг m , функция имеет в точке условный экстремум , то функция

(n+m) переменных имеет нулевые частные производные по всем своим аргументам.

ДОКАЗАТЕЛЬСТВО. Без ограничения общности полагаем, что базисный минор матрицы составляют последние m ее столбцов, т.е. переменные свободные,

а частные производные по переменным входят в базисный минор. Тогда матрица , состоящая из последних m столбцов матрицы , невырожденная и у нее есть обратная. Если в точке функция имеет условный экстремум, то ее дифференциал равен нулю при любых значения , что возможно только при

. Записав эту систему в координатной форме, получим . Последние равенства выражают нулевое значение частных производных функции по переменным

в точке . Ее производные по переменным равны в силу уравнений связи.

Функция называется функцией Лагранжа и она легко составляется по условию задачи условного экстремума.

ПРАВИЛО НАХОЖДЕНИЯ КРИТИЧЕСКИХ ТОЧЕК условного экстремума.

1. Составляют функцию Лагранжа.

2. Дифференцируют функцию Лагранжа по переменным и приравнивают нулю частные производные.

3. Полученную систему с (n +m) неизвестными

дополняют m уравнениями связи .

4. Пусть решение расширенной системы. Тогда критическая точка условного экстремума.

ЗАМЕЧАНИЕ. Для ответа на вопрос есть ли в найденной критической точке условный экстремум или его нет, требуется дополнительное исследование. Оно состоит либо из выражения части переменных через свободные переменные, подстановку их в выражение функции и переходу к решению задачи локального экстремума, либо в подстановке дифференциалов зависимых переменных в выражение второго дифференциала функции и установление знакопостоянства второго дифференциала при любых изменениях свободных переменных, например, по критерию Сильвестра.

ПРИМЕР 2. Найти стороны прямоугольника максимальной площади, вписанного в круг радиуса R .

РЕШЕНИЕ. Пусть , координаты вершины прямоугольника. Тогда нужно найти максимум функции при условии, что . Составим функцию Лагранжа и систему для определения критической точки:

. Вычитаем из второго уравнения первое : .

Решением системы в области является тройка . Из соображений существования и единственности решения задачи можно сказать, что решением служит квадрат со стороной . Формально этот результат может быть получен так :

при и , т.е.

в точке максимум.

П.2 Наибольшее и наименьшее значение функции в области.

Пусть задана функция в замкнутой области с границей - поверхностью, задаваемой уравнением с кусочно-гладкой функцией . Это означает, что граница состоит из конечного числа кусков, каждый из которых задается уравнением с дифференцируемой функцией в левой части. К границе области относятся также ребра, принадлежащие двум и более кускам границы.

Всякая непрерывная на функция принимает на ней наибольшее и наименьшее значения.

ОПР. Число А=называется наименьшим значением функции в области , если 1) 2) .

ОПР. Число В=называется наибольшим значением функции в области , если 1) 2) .

Точки и могут быть внутренними точками области или граничными.

Если точки и внутренние, то они являются критическими точками локального экстремума функции и их нахождение связано с поисками стационарных точек или точками, где не существуют частные производные функции. Если точки и принадлежат границе области , то они являются критическими точками условного экстремума. Количество налагаемых связей зависит от количества кусков поверхностей

, которым принадлежит эта точка. Все критические точки заносятся в таблицу , в которой вычисляются значения функции в этих точках. Из полученных значений выбирают наибольшее и наименьшее.

ПРИМЕР 3. Найти наибольшее и наименьшее значения функции в области

.

РЕШЕНИЕ. Найдем внутренние критические точки функцию : , или , . Первая серия имеет пересечение с только при .Во всех этих точках значение функции равно нулю.

Вторая серия не пересекается с областью . Граница содержит три куска :

1) 2) 3)

На первом куске границы и наибольшее ее значение , .

На втором куске границы . В критической точке , на границе отрезка .

На третьем куске границы функция постоянна. Таким образом, , .

УПРАЖНЕНИЕ. Приведите пример функции, у которой есть локальный максимум, но в нем функция не принимает своего наибольшего значения.

ВОПРОСЫ К ЭКЗАМЕНУ.

1. Понятие условного экстремума. Необходимое условие условного экстремума.

2. Метод множителей Лагранжа для нахождения критических точек условного экстремума.

3. Наибольшее и наименьшее значения функции нескольких переменных в ограниченной замкнутой области.