Лекции по мат. анализу / Лекция 21

Лекция 21. Несобственные интегралы.

П.1 Несобственный интеграл от неограниченной функции на конечном отрезке.

Пусть функция непрерывна на и неограниченна на каждом из интервалов

.

ОПР. Несобственным интегралом функции на отрезке называют число

.

Если несобственный интеграл существует, то говорят о сходящемся интеграле. Если предел не существует или он бесконечный, то говорят о расходимости интеграла.

ПРИМЕР 1. При каких существует интеграл ?

РЕШЕНИЕ. =, если .

Если , то . Если , то .

Таким образом, в примере 1 интеграл сходится при и расходится при .

СВОЙСТВА НЕСОБСТВЕННОГО ИНТЕГРАЛА.

1. Если интегралы и сходящиеся, то интегралы и также сходящиеся и =+,

=c.

ДОК. (следует арифметических свойств пределов).

2. Если интеграл сходящийся и - первообразная функции на , то существует и =.

ДОК. =.

3. Если функции и имеют непрерывные производные на и интегралы и сходящиеся, то справедлива формула интегрирования по частям : =.

ДОК. =().Тогда (

+=.

4. Пусть в сходящемся интеграле сделана замена переменной , с непрерывно дифференцируемой функцией , причем , . Тогда

интеграл сходящийся и справедлива формула замены переменной :

=.

ДОК. =.

5. Сходимость и расходимость интегралов и для любого одновременная.

ДОК. =. Если один из пределов существует, то существует и другой. Обратно, если один из интегралов не существует, то второй интеграл также расходится.

П. 2 Несобственные интегралы от функций .

КРИТЕРИЙ СХОДИМОСТИ.

Для сходимости интеграла , , необходимо и достаточно выполнения условия .

ДОК. В условии теоремы первообразная монотонно возрастающая функция, поскольку . Если интеграл сходящийся, то и

. Условие означает, что и - ограниченная сверху, монотонно возрастающая функция, имеющая предел при .

Тогда .

ТЕОРЕМА СРАВНЕНИЯ 1.

Если непрерывные функции и удовлетворяют условию для и интеграл сходится, то сходится интеграл .

Если интеграл расходится, то расходится и интеграл .

ДОК. и интеграл сходится по критерию. Если интеграл расходится, то и для любого 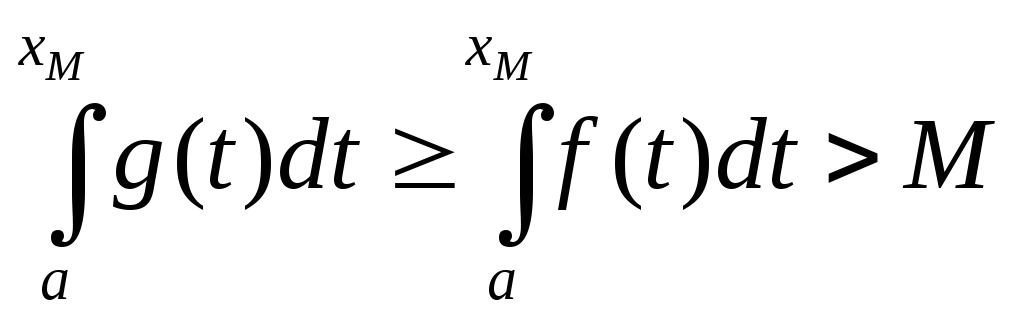, т.е. = и

интеграл по критерию расходится.

ТЕОРЕМА СРАВНЕНИЯ 2.

Если непрерывные функции и удовлетворяют условию и существует , то сходимость и расходимость интегралов и одновременная. Если , то из сходимости следует сходимость , а из расходимости следует расходимость .

ДОК. Если , то для .

По свойству 5 несобственных интегралов для сходимость или расходимость интегралов на и одновременная. На к интегралам можно применить теорему сравнения 1. Тогда из сходимости следует сходимость интеграла , а следовательно, по свойству 1 и интеграла . Аналогично, из сходимости и свойства 1 следует сходимость и по теореме сравнения 1 сходимость интеграла . Если один из интегралов, например, расходится, то по теореме сравнения 1 расходится интеграл , а, следовательно, и интеграл .

Если , то справедливо неравенство и поэтому из сходимости следует сходимость ,а из расходимости следует расходимость.

СЛЕДСТВИЕ. Если функция , , непрерывна на и неограниченна на в окрестности , причем . Тогда при интеграл

сходится, при интеграл расходится.

ДОК. Сводится к теореме сравнения 2, если и примеру 1.

ВОПРОСЫ К ЭКЗАМЕНУ.

1) Понятие несобственного интеграла от неограниченной функции. Свойства несобственного интеграла.

2) Критерий сходимости несобственного интеграла для неотрицательных функций.

3) Теоремы сравнения для несобственных интегралов.