Модуль 3

Подвижная нагрузка характеризуется непрерывным изменением места приложения вследствие перемещения по конструкции с некоторой конечной скоростью.

К нагрузкам, которые могут изменять своё положение на конструкции и которые учитываются при статическом расчёте конструкций, относится и ряд временных нагрузок. Особенностью временной вертикальной нагрузки является её непостоянное действие на конструкцию.

Опасное положение – положение, при котором требуемые величины принимают экстремальные значения.

Линия влияния – график, описывающий изменение некоторой величины, возникающей в определённом месте конструкции, в зависимости от положения, движущегося по конструкции вертикального сосредоточенного единичного груза. Каждая ордината линии влияния указывает значение величины при расположении единичного груза на конструкции над этой ординатой.

Способы построения линий влияния: статический и кинематический.

Статический способ основан на составлении уравнений равновесия для конструкции, нагруженной в произвольном месте с абсциссой x неподвижным единичным грузом, и определении из этих уравнений внутреннего усилия как некоторой функции от x . График такой функции, по определению, является линией влияния этого внутреннего усилия.

Суть кинематического способа заключается в получении очертания линии влияния без явного нахождения функциональной зависимости внутреннего усилия от абсциссы x . Такой способ основан на применении принципа возможных перемещений для определения внутреннего усилия, линию влияния которого требуется построить.

Применение линии влияния к определению внутренних усилий от неподвижных нагрузок:

Сосредоточенная сила: сосредоточенная сила P₁ Ордината линии влияния под местом приложения силы имеет некоторое значение s1 . S – усилие

Система сосредоточенных сил: ; ; ;

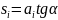Отсюда следует, что усилие равняется .

Распределённая нагрузка : , Здесь g(x) – функция, описывающая закон нагружения, s(x) –

функция, описывающая линию влияния внутреннего усилия на участке нагружения.

Если распределённая нагрузка имеет постоянную интенсивность, то её можно вынести за знак интеграла, тогда Aab – площадь линии влияния внутреннего усилия на участке нагружения.

Внешний момент: , tgα1 – тангенс угла наклона касательной к линии влияния под местом приложения к конструкции момента M1 .

Система внешних моментов:

Применение линии влияния к определению расчётных значений внутренних усилий от подвижных нагрузок:

Треугольная линия влияния. Такие очертания имеют линии влияния изгибающих моментов, а также линии влияния продольных сил, возникающих в поясах ряда ферм.

При произвольном положении двухосной нагрузки внутреннее усилие согласно описывается зависимостью . , где s1 и s2 – переменные ординаты линии влияния под левым и правым грузами подвижной нагрузки.

При произвольном положении многоосной нагрузки , Здесь Pi и si (i =1,..., k) –

силы, расположенные слева от вершины линии влияния, и соответствующие им ординаты линии влияния, а Pj и s j (i = k +1,...,n) – аналогичные величины, связанные с правым участком линии влияния.

Продифференцируем по x и получим

Внутренне усилие при движении нагрузки не достигает своего

наибольшего значения, пока первая производная не поменяет знак

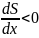
Порядок смены знаков зависит от направления движения нагрузки.

Аналитические признаки критической силы: ,

Здесь R_лев и R_пр – равнодействующие сил, расположенные слева и справа от критической силы.

Расчётное значение внутреннего усилия с учётом свойства прямолинейного участка линии влияния определяется по формуле . где s_лев и s_пр – ординаты линии влияния, соответственно, под равнодействующими сил, расположенных слева и справа от критической нагрузки.