2.2 Ефект впливу

Ефект впливу х на у визначаються як відношення приростів середніх групових цих величин :

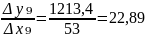
За отриманими даними можна простежити наступну тенденцію, що при збільшенні кількості наукових кадрів, обсяг виконаних наукових робіт теж збільшувався. За 2011 рік при збільшенні наукових кадрів на одиницю, обсяг наукових робіт збільшиться на 40,23 од. Проте можна зазначити, що збільшення відбувається не помірно, а стрибками. На це впливає різноманітна кількість факторів.

2.3 Коефіцієнт еластичності

Коефіцієнт еластичності є характеристикою відносної зміни у за рахунок х. Показує, на скільки процентів у середньому змінюється результат у зі зміною фактора х на 1%.

65,99* =0,24

Отже, збільшення кількості наукових кадрів на 1% призводить до збільшення обсягу виконаних наукових робіт на 24%.

2.4 t-критерій Стю’дента для коефіцієнта регресії фактичний та критичний

Коефіцієнт регресії у невеликих за обсягом сукупностях схильний до випадкових коливань, тому перевіримо його істотність за допомогою t-критерію Стьюдента:

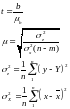
Для його визначення спочатку розрахуємо стандартну (середню) похибку коефіцієнта спочатку розрахуємо стандартну (середню) похибку коефіцієнта регресії:

Для лінійної функції m=2. За данними таблиці 2.1 маємо:

2336924

А залишкова дисперсія становить:

Так як маємо два параметри рівняння регресії, тоді

Звідси

, що значно перевищує критичне значення 1, 86 з ймовірністю 0,95.

t_{фактичне}= 8,45

t_{критичне}= t_0,95(8)= 1,86

t_{фактичне}>t_{критичне}

Гіпотеза про випадковий характер коефіцієнта регресії відхиляється, а отже, можна зробити висновок, що вплив кількості наукових кадрів на обсяги вироблених наукових робіт є істотним.

2.5 Лінійний коефіцієнт кореляції Пірсона

Оцінимо щільність зв’язку між кількістю наукових кадрів та вироблених ними робіт за допомогою лінійного коефіцієнта кореляції Пірсона. Даний коефіцієнт набуває значень у межах +- 1. Він характеризує не тільки щільність зв’язку, а й його напрям.

Доцільною формулою для розрахунку є:

Використовуємо дані таблиці 2.1:

6262210,07– факторна дисперсія, що вимірює варіацію у, зумовлену лише впливом фактора х.

- залишкова дисперсія, що визначає відхилення у від теретичних значень У, характеризує вплив на результативну ознаку всіх інших факторів, окрім х.

7085115,87

2336924

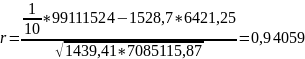
Отже, коефіцієнт кореляції за розрахунками становить 0,94, що говорить про щільний зв'язок між кількістю наукових кадрів і обсягом наукових робіт. Значення є додатнім, таким чином, наявний прямий зв'язок між заданими ознаками.

2.6 Коефіцієнт детермінації показує відношення факторної дисперсії до загальної розглядається як міра щільності кореляційного зв’язку.

R²= 0,883854292

Це означає що 88,38% варіації обсягу наукових робіт залежить від варіації кількості наукових кадрів , а 11,62% припадає на інші фактори. Даний зв'язок є щільним.

Можна перевірити істотність кореляційного зв’язку. Для цього необхідно порівняти фактичне з критичним. Ступені свободи в нашому випадку дорівнюють:

Критичні значення характеристик щільності для та становить . Обчислений коефіцієнт перевищує критичне значення, що з ймовірністю 95% підтверджує істотність зв’язку між кількістю наукових кадрів та обсягів вироблених наукових робіт.

2.7 F-критерійфактичний та критичний

Критерій Фішера функціонально пов'язаний з коефіцієнтом детермінації та розраховується за формулою:

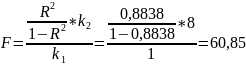
Критичне значення критерію Фішера є 5,32, фактичне значно його перевищує та становить 60,85. Отже, даний зв'язок між моделями є істотним.

Можна зробити висновок, що при розрахунках коефіцієнтів кореляції, детермінації, F-критерію Фішера, t-критерій Стю’дента, ми отримали такі показники, що вказують на прямий, досить щільний, істотний зв'язок між заданими даними.