1)Комплексные числа

Комплексное число – расширение понятие числа. Ранее мы представляли себе числа как прямую. С введением понятия комплексных чисел мы представляем число как плоскость, где одна прямая – ось реальных чисел, вторая – ось мнимых чисел. Таким образом, лежащая на первой прямой точка – реальное число, на второй – мнимое, не принадлежащая ни одной из них – комплексное число.

Комплексное число имеет вид a+bi, где а – реальное число, bi – мнимое.

Мнимое число в свою очередь состоит из реального числа b помноженного на мнимую единицу i, представляющую собой .

С комплексными числами можно выполнять действие, как то:

• Сложение и вычитание. В данном случае результатом будет комплексное число, коэффициенты a и b которого являются суммой или разностью коэффициентов a и b исходных чисел.

• Умножение. В данном случае числа перемножаются как произведение двух сумм.

• Деление. В данном случае числитель и знаменательно домножаются на знаменатель.

• Сравнение. Сравниваются значение a и b попарно.

2)Свободные векторы, их сложение и умножение на число

Вектор – направленный отрезок.

Свободный вектор – вектор, который может свободно переноситься в пространстве. Таким образом, если в пространстве есть два вектора, модуль и направление которых одинаковы, а начало и конец не совпадают, то данные вектора являются равными.

При умножении вектора на число его модуль домножается на заданное число, направление остаётся прежним.

При сложении двух векторов получается вектор, координаты которого являются суммой координат исходных векторов. Это очень легко иллюстрировать при помощи стандартного метода треугольника – начало второго вектора переносится в конец первого. Результатом будет вектор, имеющий начало первого и конец второго.

3)Декартов базис, составляющие вектора по оси и его проекция на ось

Базис — множество таких векторов в векторном пространстве, что любой вектор этого пространства может быть единственным образом представлен в виде линейной комбинации векторов из этого множества — базисных векторов.

Декартов базис представляет собой набор векторов i,j,k, где каждый из представленных векторов является единичным положительным отрезком на осях x,y,z.

В данном случае любой вектор можно разложить по базису – представить его как сумму вышеуказанных векторов.

Проекция же вектора на ось в таком случае является количеством соответствующих единичных векторов.

4)Скалярное произведение векторов

Скалярное произведение векторов – произведение, дающее как результат скаляр.

Ему соответствует умножение длины первого вектора на проекцию на него второго вектора (или наоборот).

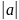
Записывается как или a  b или (a,b) и элементарно определяется как  cos(a,b).

В данной формуле a и b можно свободно менять местами.

Если скалярное произведение двух элементов пространства равно нулю, то они называются ортогональными друг другу.

5)Векторное произведение векторов

Векторное произведение векторов – произведение, дающее как результат вектор, перпендикулярный плоскости первых двух векторов. Причём длинна данного вектора будет равна произведению модулей первых двух векторов, помноженных на синус угла между ними.

Записывается как [a,b] или axb.

Геометрический смысл: даёт площадь параллелограмма, построенного на данных векторах.

Свойства:

• Если [a,b] равно c, то [b,a] равно –с.

• Свойство ассоциативности: c[a,b]=[ca,b]=[a,cb].

• Свойство дистрибутивности: [a+b,c]=[a,c]+[b,c].

• Тождество Лагранжа: [a, [b,c]]=b(a,c)-c(a,b).

• 

• Векторное произведение вектора на самого себя (либо на коллинеарный себе вектор) даёт 0.