
- •Электротехника.
- •Электрические цепи. Элементы электрической цепи постоянного тока. Генераторы энергии. Виды электрических соединений. Приемники электрической энергии.
- •Уравнение электрического состояния цепи (Закон Ома и Кирхгофа). Примеры расчета электрических цепей. Параметры электрических цепей. Баланс мощностей.
- •Методы расчета электрических цепей. Метод контурных токов, узловых потенциалов, наложения и двух узлов. Примеры расчета сложных цепей.
- •1. Линейные цепи однофазного синусоидального тока.
- •8 .Последовательное соединение резистивного, индуктивного и емкостного элементов в цепи синусоидального тока.
- •7. Переходные процессы в электрических цепях. Законы коммутации.
1. Линейные цепи однофазного синусоидального тока.
Е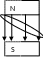 сли
напряжение и токи измен-ся во времени
по синусоидальному закону, то они наз
синусоидальными (гармоническими).
Линейные ЭЦ, в кот сопротивление,
индуктивность и емкость не зав от
значений и направлений токов и напряжений
цепи..
2.
Процесс возникновения синусоидальной
ЭДС в простейшем генераторе
сли
напряжение и токи измен-ся во времени
по синусоидальному закону, то они наз
синусоидальными (гармоническими).
Линейные ЭЦ, в кот сопротивление,
индуктивность и емкость не зав от
значений и направлений токов и напряжений
цепи..
2.
Процесс возникновения синусоидальной
ЭДС в простейшем генераторе
С
w
игналов. Рассмотрим проводник в виде прямоугольной рамки вращ с постоян угловой скоростью W в постоян однородном маг поле. Где мгновенное значение sin ф-ции, т.е зн-е величины в данный момент времени e = Em* Sin(wt+ψe) где Em – амплитуда- мах зн-е функции за период, wt+ψe – аргумент ф-ции (фаза или фаз переход). Фаза отчитывается от точки перехода син ф-ции ч/з «0» положительного значения. Все это Графическое представление син ф-ции. 3. Параметры синусоидальных токов и напряжений. Каждая син Ф-ция времени однозначно опр тремя пар-ми: 1) Em, Im, Um; 2) W [рад/сек]- угловая частота – скорость изменения аргумента син ф-ции 3) ψi, ψu, ψe – начальн угол сдвига фазы, т.е. зн-е аргумента син ф-ции в момент времени t=0. отсюда: u(t) = Um Sin(wt +ψu); i(t) = Im Sin(wt +ψi). Также хар-ся: 1) T= 2π/w, наименьш интервал времени, по истечению кот зн-ия ф-ции повторяются; 2) f=1/T частота сети – число периодов в ед времени fпром цепи=50Гц; φ=φu-φi угол сдвига фазы между напр и током; 3) Действующее зн-е син ф-ции – это такой пост ток, кот на резисторе с сопр R за период выделяет такое кол тепла как: I²RT = ∫ от 0 до T *i²Rdt= (I²m/2)*TR; Iдействующее=Im/√2 ; Uд=Um/√2; Eд=Em/√2; 4)среднее зн-е ф-ции под кривой за ½ периода Iср(Eср, Uср)=1/ T/2 ∫ от0 до T/2 idt=2/πIm Все это Аналитическое представление син ф-ции, когда запис зн-я ф-ции, по кот мон опр пар-ры ф-ции. 4. Векторное изо электрич величин. Угол сдвига фазы φ между I и U.5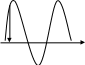 .
Комплексное представление электрических
величин.
I'=Icos
Ψ0+jIsin
Ψi
(тригонометрическая запись) = Iaктивн
+jIреактивн
(алгебраич форма) = Ie
в степени j
Ψi
(паказательная запись) от сюда: I
=√(Ia)²
+ (Ib)²
6.
Законы
Кирхгофа в комплексной форме.
Комплексн м позволяет исп-ть все средства
анализа и расчета син цепей. Особая роль
отводится правилам Кирхгофа из-за их
универсальности. 1-е правило:в любом
узле k
электрич цепи алгебраич сумма n
комплексов токов равна нулю Σİ k
= 0. Правило Законов: втекающие в узел
токи в алгебраич сумме берутся со знаком
«+», вытекающие со знаком «-». 2-е правило:
в люб контуре цепи алгебраич сумма m
комплексов ЭДС равна алгебраич сумме
m
комплексов падений напряжений вдоль
этого контура: ΣĖ k
(m)
=Σİ k*Ż
k
(n).
Правило знаков: если направление ЭДС и
падения напряжения совпадает с заданным
направлением обхода, то в алгебраич
сумме они берутся со знаком «+», в
противном случае «-».
.
Комплексное представление электрических
величин.
I'=Icos
Ψ0+jIsin
Ψi
(тригонометрическая запись) = Iaктивн
+jIреактивн
(алгебраич форма) = Ie
в степени j
Ψi
(паказательная запись) от сюда: I
=√(Ia)²
+ (Ib)²
6.
Законы
Кирхгофа в комплексной форме.
Комплексн м позволяет исп-ть все средства
анализа и расчета син цепей. Особая роль
отводится правилам Кирхгофа из-за их
универсальности. 1-е правило:в любом
узле k
электрич цепи алгебраич сумма n
комплексов токов равна нулю Σİ k
= 0. Правило Законов: втекающие в узел
токи в алгебраич сумме берутся со знаком
«+», вытекающие со знаком «-». 2-е правило:
в люб контуре цепи алгебраич сумма m
комплексов ЭДС равна алгебраич сумме
m
комплексов падений напряжений вдоль
этого контура: ΣĖ k
(m)
=Σİ k*Ż
k
(n).
Правило знаков: если направление ЭДС и
падения напряжения совпадает с заданным
направлением обхода, то в алгебраич
сумме они берутся со знаком «+», в
противном случае «-».
7. Резистивный элемент в цепи синусоидального тока. Компактные Ур-я в действительной и комплексной форме
Индуктивный элемент в цепи синусоидального тока Xα = W *α [Ом].
Емкостный элемент в цепи синусоидального тока X с = 1/ W*C
8 .Последовательное соединение резистивного, индуктивного и емкостного элементов в цепи синусоидального тока.
I общий, U складывается векторно или в комплексном виде
Ż = R+j(Xα - X с) – полное комплексное сопротивление цепи. 9. При последовательном соед-ии Эл-ов построение векторной диаграммы следует начинать с вектора тока, т.к он явл общим для всех эл-ов цепи. 10.Резонанс напряжений: Xα = X с . Резонанс – это такое состояние электрич цепи, состоящий из разнохарактерных реактивных эл-ов, при кот фазовый сдвиг между входным током и приложенным напряжением = 0. Цепи в кот возникает явление резонанса наз колебательными контурами(резонансные цепи). Можно получить при последовательном соед-ии: Xα = W *α и X с = 1/ W*C; изменяя α или с получаем W0= 1/ √α*С – резонансная частота. Сопротивл реактив Эл-та при резонансн частоте наз характерестическое сопрот послед-ого колебат контура ρ = W0 * α = 1/ W0 * C = √α/ C.
11.Параллельное соединение приемников в цепи синусоидального тока. u=Um Sin(wt +ψu); Imk = Um/R = Um*G; Imα = Um/Xα = Um*Bα –реактивная проводимость; Imc = Um/Xc = Um*Bc ; Полная проводимость Ψ= √G² + B² ; B = X/Z² ; Полная комплексная проводимость Ý = 1/ Ż Проводимость цепей синусоидального тока – величина обратная сопротивлению G [См] сименс.
12.
Параллельный колебательный контур.
Резонанс токов.
Цепи
в которых возникло явление резонанса
наз колебательными контурами или
резонансными цепями. Резонансом токов
называют такой режим параллельного
колебательного контура, при котором
фазовый сдвиг между напряжением на его
выводах и общим током равен нулю (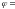 0).
А мощность, потребляемая из сети, равна
активной мощности контура. Реактивная
мощность при резонансе из сети не
потребляется.
0).
А мощность, потребляемая из сети, равна
активной мощности контура. Реактивная
мощность при резонансе из сети не
потребляется.
 .
Комплекс эквивалентной полной проводимости
параллельного колебательного контура:
.
Комплекс эквивалентной полной проводимости
параллельного колебательного контура: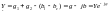 ,
где
,
где
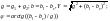 где
где
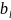 и
и
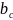 -
индуктивная и емкостная проводимость;
у - полная проводимость цепи; g –
проводимость резистивного элемента
-
индуктивная и емкостная проводимость;
у - полная проводимость цепи; g –
проводимость резистивного элемента
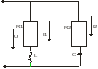
Условия
возникновения резонансов токов: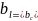 ;
;
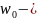 резонансная
частота при резонансе токов.
резонансная
частота при резонансе токов.
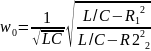
Особенности поведения цепи при резонансе токов:
φ= 0I в неразветвленной части цепи -> min (в идеале 0)
Реактивные мощности
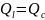 .
Между катушкой и конденсатором происходит
обмен энергиями,но источник питания в
этом обмене не учавствует. Источник
питания только восполняет необратимые
потери на активных элементах.
.
Между катушкой и конденсатором происходит
обмен энергиями,но источник питания в
этом обмене не учавствует. Источник
питания только восполняет необратимые
потери на активных элементах.
3)Резонансная
частота
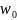 при резонансе токов зависит не только
от параметров реактивных элементов,но
и активных сопротивлений
при резонансе токов зависит не только
от параметров реактивных элементов,но
и активных сопротивлений
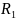 и
и
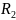 .
.
4)Резонанс токов возможен если и не равно ρ.
5)Если
и
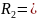 ρ,то резонанс получается на любой
частоте.
ρ,то резонанс получается на любой
частоте.
При
резонансе токов
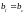 и, следовательно, равны между собой
реактивные токи
и, следовательно, равны между собой
реактивные токи
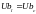 ,
или
,
или
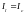 ,
которые находятся в этом случае в
противофазе. При резонансе токов возможны
ситуации, когда реактивные токи
,
которые находятся в этом случае в
противофазе. При резонансе токов возможны
ситуации, когда реактивные токи
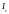 и
и
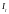 намного
превышают суммарный ток в цепи, вследствие
чего резонанс при параллельном соединении
называют резонансом токов. Это возможно
при условии
намного
превышают суммарный ток в цепи, вследствие
чего резонанс при параллельном соединении
называют резонансом токов. Это возможно
при условии
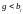 или
или
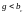
Отношение
индуктивного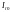 или емкостного
или емкостного
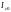 токов при резонансе токов к суммарному
току
токов при резонансе токов к суммарному
току
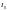 называют добротностью параллельного
колебательного контура:
называют добротностью параллельного
колебательного контура:
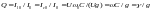
Затухание
в параллельном контуре, как и в
последовательном контуре, есть величина,
обратная добротности:
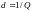
нету
нету.
