14. Использование платежной матрицы и метода парето для выбора альтернатив решений.

Важнейшим условием существования задачи принятия решений является наличие нескольких допустимых альтернатив из которых нужно в некотором смысле лучшую.

Метод платежной матрицы используется в ситуациях наличия множества критериев и возможности сведения результатов оценки альтернатив и некоторой единой оценке. Задача формируется следующим образом. Имеется набор альтернатив {A_i}, 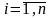; альтернативы оцениваются множеством критериев {K_j}, 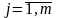. Результаты оценки альтернатив по критериям {R_ij}. Каждая альтернатива характеризуется разнородными результатами и если их удается свести к единой оценки O_ij (чаще всего стоимостной), то выбор альтернативы можно произвести с помощью платежной матрицы (табл. 4).

Таблица 4. Платежная матрица

Аi	Kj					∑
	K1	K2	…	Km
А1	D11	D12	…	D1m	∑D1m
А2	D21	D22	…	D2m	∑D2m
…	…	…	…	…	…
Аn	Dn1	Dn2	…	Dnm	∑Dnm

Лучшей альтернативой будет та, которая имеет максимальную сумму оценок А^* = maх ∑D_ij.

Использование метода Эдворта–Парето основано на понятии доминирования альтернатив. Альтернатива А₁ является доминирующей по отношению к альтернативе А₂, если по всем критериям оценки альтернатива А₁ не хуже, чем альтернатива А₂, а хотя бы по одному критерию оценка А₁ лучше. При этом альтернатива А₂ будет доминируемой. Один из возможных способов решения задачи состоит в попарном сравнении альтернатив и исключения доминируемых. Таким образом получаем множество Эдворта–Парето (недоминируемых) альтернатив. Задача эта обычно рассматривается как предварительная. Далее решается задача выбора решения – единственной альтернативы из множества Эджворта–Парето.

15. Использование теорий статических решений и таблиц решений для выбора альтернатив

Довольно большую группу методов выбора представляет теория статистических решений, позволяющая принимать решения в условиях неопределенности.

Пусть {K_j} – множество критериев, ; {A_i} – множество альтернатив, ; {P_j} – множество вероятностей критериев; {Э_ij} – оценки эффективности i – ой альтернативы по j – му критерию. Для решения задачи строится исходная матрица эффектов (табл. 5).

Таблица 5. Матрица эффектов

Аi	Kj				min Эij		max Эij
	К1	К2	…	Кm
А1	Э11	Э12	…	Э1m
А2	Э21	Э22	…	Э2m
..	…	…	…	…
Аn	Эn1	Эn2	…	Эnm

Выбор зависит от особенностей ЛПР, эта особенность учитывает отношения ЛПР к статистич природному риску. Выделяют 3 типа ЛПР:

1)ЛПР не склонное к риску – опасается много проиграть, основное внимание уделяет на наихудшие результаты.

2)Склонные к риску, кот боятся мало выиграть, основное внимание уделяет на наилучшие результаты или потенциальные потери.

3)ЛПР безразличен к риску – уделяет одинаковое внимание наилучш и наихудш результатам – взвешенное отношение к риску.

Метод Уолда (максимальный) ориентирует на выбор наихудших результатов по каждой альтернативе и выбор альтернативы, приводящей к наилучшему из худших результатов: max (min Э_ij).

Метод Уолда определяет стратегию – «рассчитывай на лучшее», являющейся довольно осторожной. Более смелая стратегия выбирается с помощью метода Сэвиджа, определяющего, что оптимальной будет альтернатива, для которой максимальный риск при различных стратегиях окажется минимальным. При этом используется не величина эффекта, а величина предполагаемых потерь, рассчитываемая по разнице между наибольшим эффектом, достигаемым при правильном выборе для данного критерия, и ошибочным решения (минимакс):

,

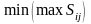где S_ij = max Э_ij – Э_ij.

Метод Гурвица позволяет выбрать альтернативу между крайними пессимистическими и оптимистическими стратегиями в зависимости от показателя пессимизма 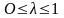. При этом 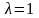соответствует крайнему пессимизму, а 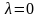- крайнему оптимизму. Значение 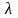назначается ЛПР.

Формула для выбора по Гурвицу:

.

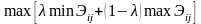Метод Лапласа рассчитан на среднюю величину

.

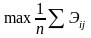Необходимо отметить, сто использование различных методов теории статистических решений дает и весьма различные результаты. Достоинством же этих методов является то, что они дают определенную свободу выбора для ЛПР. В реальной жизни существует огромное количество стратегий, когда эффективные результаты выбора могут быть получены с помощью экспертных методов.