
- •Краткий конспект лекций к первой части курса «Теоретические основы электротехники»
- •Введение
- •Общие определения цепей и их параметров
- •Активные элементы
- •Свойства линейных электрических цепей
- •Основные уравнения электрических цепей. Законы Кирхгофа.
- •Линейные цепи постоянного тока
- •Эквивалентные преобразования пассивных цепей
- •Расчет цепей по законам Кирхгофа
- •Метод контурных токов
- •Метод узловых напряжений
- •Метод наложения
- •Свойство взаимности
- •Теорема о компенсации
- •Метод эквивалентного источника напряжения (теорема Гельмгольца-Тевенена)
- •Метод эквивалентного источника тока (теорема Нортона)
- •Потенциальная диаграмма.
- •Баланс мощностей
- •Топология электрической цепи
- •Топологические матрицы графов
- •Линейные цепи с источниками гармонических эдс и токов Периодические напряжения и токи
- •Генератор синусоидального напряжения
- •Временная диаграмма
- •Векторная диаграмма
- •Действующие и средние значения периодических эдс и токов
- •Установившийся режим в цепи с последовательным соединением активного сопротивления, индуктивности и емкости
- •Установившийся режим в цепи с параллельным соединением активного сопротивления, индуктивности и емкости
- •Энергетические соотношения в цепях синусоидального тока
- •Комплексный метод расчета электрических цепей
- •Комплексные сопротивления и проводимости
- •Основные законы электрических цепей в комплексной форме
- •Мощность в комплексной форме. Баланс мощностей
- •Резонансные явления в электрических цепях. Частотные характеристики.
- •Резонанс напряжений
- •Частотные характеристики последовательного r-l-c контура.
- •Резонансные характеристики
- •Параллельный колебательный контур. Резонанс токов.
- •Резонансные кривые при параллельном соединении элементов
- •Цепи с взаимной индукцией
- •Последовательное и параллельное соединения индуктивно связанных катушек
- •Трансформатор без стального сердечника
Баланс мощностей
Вытекает из закона сохранения энергии. Условие энергетического баланса для любой электрической цепи постоянного тока выражается в виде равенства нулю суммы мощностей по всем элементам:
 ,
где п - число
элементов схемы.
,
где п - число
элементов схемы.
Уравнение баланса мощностей можно записать в иной форме:
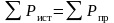 .
.
Суммарная мощность, развиваемая источниками электрической энергии, равна суммарной мощности, потребляемой приемниками.
Первая обычно называется генерируемой мощностью, а вторая – потребляемой.
Потребляемая
энергия в цепях постоянного тока связана
с выделением на сопротивлениях при
протекании тока теплоты и определяется
в соответствии с законом Джоуля – Ленца:
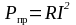 .
.
Для
идеального источника напряжения
генерируемая мощность определяется
как
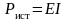 ,
причем если направление тока совпадает
с направлением ЭДС, то произведение
берется со знаком «+». Это означает, что
источник ЭДС доставляет в цепь энергию.
,
причем если направление тока совпадает
с направлением ЭДС, то произведение
берется со знаком «+». Это означает, что
источник ЭДС доставляет в цепь энергию.
Если
направление тока встречно направлению
ЭДС, то источник не поставляет энергию,
а потребляет ее (например, идет заряд
аккумулятора). При этом произведение
 в уравнение энергетического баланса
входит со знаком «−».
в уравнение энергетического баланса
входит со знаком «−».
|
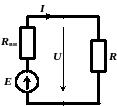
Если источник неидеальный, то
|
Для источника тока
|
Если
направление тока источника совпадает
с направлением напряжения, то
|
Топология электрической цепи
Топология – область математики, изучающая свойства геометрических фигур. Топологические методы расчета электрических схем основаны на аналитическом, либо на геометрическом способах описания свойств графа, изображающего электрическую цепь.
Аналитическое описание свойств графа основывается на теории матриц и определителей. Геометрическое описание использует правила преобразования графов.
Граф – это условное графическое изображение схемы, в которой его ветви (p) и узлы (q) соответствуют ветвям и узлам схемы.
Перед составлением топологических матриц, ветви схемы (графа) нумеруют и ориентируют стрелками. Стрелки указывают положительные направления для отсчета тока и напряжения на каждой ветви. Такой граф называется направленным или ориентированным.

При описании графов цепей используют следующие топологические понятия.
Путь графа - непрерывная последовательность ветвей, проходящих не более одного раза через каждый узел. Для приведенного графа между узлами 2 и 3 путь образуют следующие ветви: 2; 5-3; 1-4-3; 1-6; 5-4-6.
Контур - замкнутый путь графа, в котором совпадают начало и конец. Например, для приведенного графа: 1-4-5; 1-2-3-4; 4-3-6 и т.д.
Если между любой парой узлов графа существует путь, то граф называется связанным.
Дерево графа – любая совокупность ветвей графа, соединяющих все его узлы без образования контуров.
Дерево связанного графа с q узлами содержит (q−1) ветвь, например:

Ветви графа, не вошедшие в выбранное дерево, называются ветвями связи (показаны пунктиром).
Количество ветвей связи: p − (q − 1).
Сечение графа - совокупность ветвей, рассечение которых делит граф на два изолированных подграфа.
Главное сечение графа содержит ветви связи и лишь одну ветвь дерева, номер которого соответствует номеру сечения.

Главный контур (независимый контур) – это контур, образованный ветвями дерева и одной ветвью связи (количество главных контуров равно количеству ветвей связи). Направление контура определяется направлением ветви связи, образовавшей данный контур.


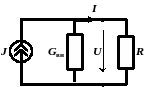
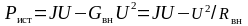 .
.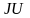 берется со знаком «+», в противном
случае – со знаком «−».
берется со знаком «+», в противном
случае – со знаком «−».