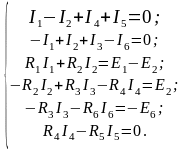Линейные цепи постоянного тока

Основной задачей расчета электрической цепи является ее анализ, который заключается в определении токов, напряжений и мощностей по заданным их сопротивлениям и источникам электрической энергии. Для линейных цепей эти задачи имеют однозначное решение, которое получают в результате составления и решения системы алгебраических уравнений согласно законам Кирхгофа, Ома и Джоуля-Ленца.

В цепи постоянного тока ; .

Т.о. при протекании в цепи постоянного тока, его величину определяют только резистивные элементы.

Эквивалентные преобразования пассивных цепей

1. Последовательное соединение – по 2-му закону Кирхгофа.

, , .

2. Параллельное соединение – по 1-му закону Кирхгофа.

, , .

3. Смешанное соединение

. Формула токового делителя: , .

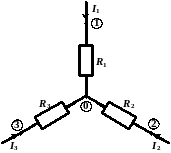
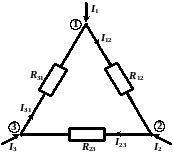
4. Преобразование из «треугольника» в «звезду» и обратно.

соединение «звездой»	соединение «треугольником»

Преобразование называется эквивалентным, при котором напряжения и токи в остальной части схемы сохраняются неизменными.

Формулы преобразований могут быть получены, используя законы Ома и Кирхгоффа:

; ; .

; ; .

Расчет цепей по законам Кирхгофа

Обычно заданными являются величины и направления ЭДС источников напряжения и внутренних токов источников тока, а также зна­чения всех внутренних и внешних сопротивлений или проводимостей. Определению подлежат токи и напряжения ветвей. Поэтому число неизвестных равно числу р ветвей схемы и, следовательно, столько же независимых уравнений требуется составить по первому и второму законам Кирхгофа.

Уравнения, составленные по первому закону Кирхгофа для цепи с q узлами, будут независимыми лишь для узлов, так как урав­нение для последнего узла будет следствием предыдущих. Следовательно, по второму закону Кирхгофа требуется составить независимых уравнений.

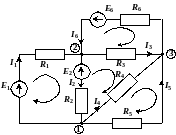
Пример составления системы уравнений.

Изображенная на рисунке цепь имеет 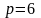ветвей и узла. Следовательно, необходимо иметь систему из шести уравнений. При этом по первому закону Кирхгофа требуется составить 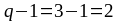уравнения, а по второму закону 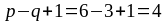уравнения.

Решая систему уравнений любым известным из алгебры способом, находят все неизвестные токи ветвей. Отрицательный знак указывает на то, что действительное направление тока противоположно выбранному направлению.

Достоинством рассмотренного метода является его общность, а недостатком – громоздкость алгебраических преобразований при отыскании неизвестных. Поэтому зачастую применяют специальные методы расчета сложных цепей, которые сводятся либо к упрощению схемы (методы наложения и эквивалентного источника энергии), либо к уменьшению числа неизвестных (методы контурных токов и узловых напряжений).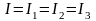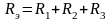
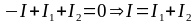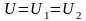
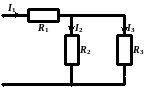
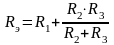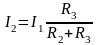
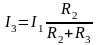
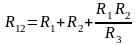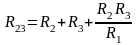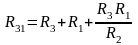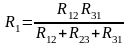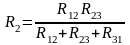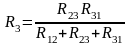