Комплексные сопротивления и проводимости

Отношение комплексного напряжения к комплексному току называют комплексным сопротивлением цепи и обозначают .

,

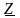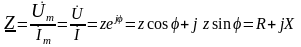где R, X и z – активное, реактивное и полное сопротивления цепи.

С другой стороны:

.

Тогда полное сопротивление z получим из соотношений:

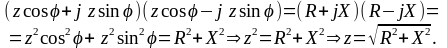
В случае последовательного соединения элементов R,L,C комплексное сопротивление запишется в виде:

.

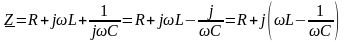Отношение комплексного тока к комплексному напряжению называют комплексной проводимостью цепи и обозначают :

,

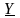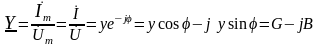где 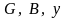– активная, реактивная и полная проводимости цепи.

Поскольку комплексная проводимость есть величина обратная комплексному сопротивлению, то:

.

Пусть: ; .

Тогда: .

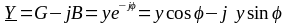С другой стороны: .

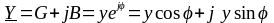Тогда полную проводимость у получим из соотношений:

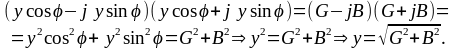
В случае параллельного соединения элементов G,L,C комплексная проводимость запишется в виде:

.

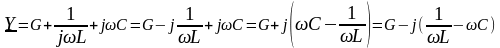Очевидно, что .

Перевод комплексных величин в показательную форму:

3 + j2

1. Находим модуль: .

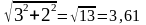2. Находим аргумент: .

Окончательно: .

3 − j2

1. Находим модуль: .

2. Находим аргумент: .

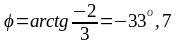Окончательно: .

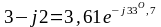Перевод показательных величин в комплексную форму:

;

.

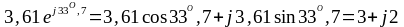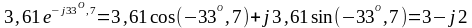Основные законы электрических цепей в комплексной форме

Законы электрических цепей переменного тока в комплексной форме имеют такой же вид, как и для цепей постоянного тока, с заменой соответствующих постоянных величин комплексными: , , , , , .

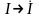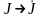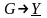Закон Ома в комплексной форме имеют вид: .

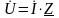Достоинство этих выражений заключается в том, что в них учи­тывается как связь между действующими значениями тока и напряжения, так и сдвиг фаз между ними.

Первый закон Кирхгофа в применении к узлу: .

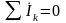Второй закон Кирхгофа применительно к контуру: .

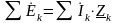Возможность использовать соотношения для цепей постоянного тока справедлива и для эквивалентных преобразований.

При после­довательном соединении комп­лексное сопротивление всей цепи равно алгебраической сумме комплексных сопротивлений от­дельных ее участков: .

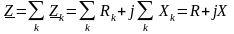При параллельном соединении комплексная проводимость всей цепи равна алгебраической сумме комплексных проводимостей отдельных ее участков:

.

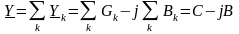При смешанном соединении:

; , . , .

Расчет сложных цепей переменного тока комплексным методом осуществляется с помощью тех же методов, что и цепей постоянного тока при замене соответствующих величин их комплексными аналогами.

Мощность в комплексной форме. Баланс мощностей

В качестве комплексной мощности понимают произведение комплексного напряжения на сопряженную комплексную величину тока. В ре­зультате чего, получаем комплексную мощность:

.

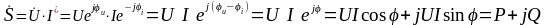Вещественная часть комплексной мощности равна активной мощности Р, а мнимая часть Q (без j) реактивной мощности. Модуль комплексной мощности равен полной мощности .

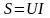Баланс мощности:

1. Сумма комплексных мощностей для всех ветвей электрической цепи равна 0.

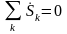, откуда .

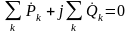Такое равенство возможно только в том случае, есл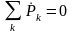и и .

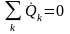2. Поскольку в каждой цепи есть источники и приемники, то

Источники ЭДС и токов можно разделить:

.

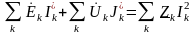Действительно, мощность, потребляемую приемником, мы можем представить как:

.

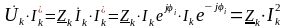С другой стороны,

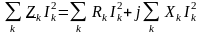
и для мощности источников

.

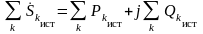Следовательно, 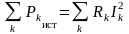и .
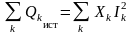
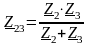
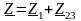
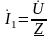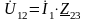
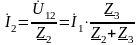
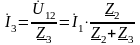