Методика расчета

1. Определение параметров частицы.

Начальная энергия рассчитывается по следующей формуле:

(9)

m – масса частицы;

V₀ – начальная скорость;

g – ускорение свободного падения (9,8 м/с²);

h – высота на которой находится частица при попадании в конденсатор (h=d–h₀).

2. Определение параметров конденсатора.

Емкость конденсатора из (6.8):

(10)

Величина емкости определяется также геометрией конденсатора и диэлектрическими свойствами среды, заполняющими пространство между обкладками.

Из формулы для ёмкости плоского конденсатора найдём расстояние между обкладками:

(11)

С – электроемкость плоского конденсатора;

₀ – диэлектрическая проницаемость вакуума, ₀= Ф/м;

 – относительная диэлектрическая проницаемость вещества заполняющего зазор, =1 (воздух);

S – площадь пластины, S=l² ;

l – длина пластины.

Величина напряжения из (2):

(12)

Подставив (12) в (10) находим электроемкость:

(13)

Оценим численные значения сил, действующих на частицу:

(14)

Подставим (14) в (4):

(15)

Выполнение расчетов

1.

Проверка размерности:

.

2.

Проверка размерностей

3.

_{Проверка размерностей:}

4. = =

=1,822∙10^-18 Дж;

Проверка размерностей:

Вычислим по формуле (15):

Вычислим по формуле (5):

Получили:

Поэтому в дальнейших расчётах силой тяжести можно пренебречь, и считать, что заряженная частица в конденсаторе движется только под действием электрических сил, то есть:

Определение графических зависимостей

Определение графической зависимости V(x):

1. Вдоль оси Ох заряд движется равномерно ( =0):

(16)

2. Вдоль оси Oy заряд движется равноускоренно под действием постоянной электрической силы:

3. Скорость частицы

- по оси Ох: (17)

- по оси Оу: (18)

4. Скорость частицы

(19)

5. Из (16) находим:

(20)

6. Подставим (20) в (19):

Получили зависимость:

7. Электрическая сила: F=qE, где Е – напряженность электрического поля в конденсаторе, Е=U/d. Используя второй закон Ньютона найдем ускорение частицы:

(21)

8. Следовательно:

; V = 8·10¹⁰x + 991465

9. Тогда время полета . Теперь найдем координату «х» падения: , она равна , но l = 50 см, следовательно, частица упадет на пластину, поэтому ее скорость будет равна нулю. На графике это будет прямая линия, лежащая на оси х. На графике скорость в , координата х в мм.

График зависимости V(x):

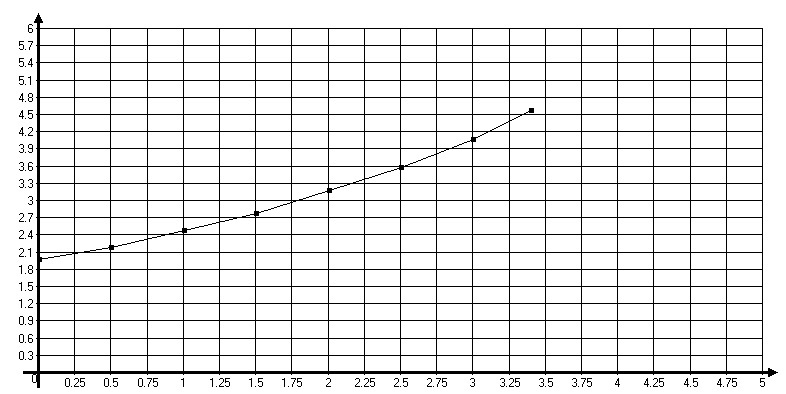
	2	2,2	2,5	2,8	3,2	3,6	4,05	4,6
	0	0,5	1	1,5	2	2,5	3	3,4

Определение графической зависимости а_n(t):

1. Полное ускорение , где – являются проекциями на направление соответственно нормали и касательной проведенной в точке (см. рис. 2). Модуль нормального ускорения:

, где (22)

V – модуль скорости, V_x – проекция вектора скорости на Ох

(23)

п

(24)

(25)

одставив (21) в (18):

Решив совместно 22–25 равенства, получим зависимость нормального ускорения от времени:

; a_n = 2·10⁶·t^-1:

График зависимости a_n(t):

*10¹³ а_n, м/с²

t *10-7 с	an *1013 an
0,3	6,44
0,6	3,22
0,9	2,15
1,2	1,61
1,5	1,29
1,8	1,07
2,1	0,92
2,4	0,81

*10^-7 t, c