6. Электрическая емкость конденсатора.

Физическая величина, определяемая отношением заряда q одной из пластин конденсатора к напряжению между обкладками конденсатора, называется электроемкостью конденсатора:

. (6.1)

При неизменном расположении пластин электроемкость конденсатора является постоянной величиной при любом заряде на пластинах.

Единица электроемкости. Единица электроемкости в международной системе — фарад (Ф). Электроемкостью 1 Ф обладает такой конденсатор, напряжение между обкладками которого равно 1 В при сообщении обкладкам разноименных зарядов по 1 Кл. .

Электроемкость плоского конденсатора. Напряженность   поля между двумя пластинами плоского конденсатора равна сумме напряженностей полей, создаваемых каждой из пластин:

 .

Если на пластинах площадью S находятся электрические заряды + q и - q, то на основании формул (38.5) и (38.6) для модуля напряженности поля между пластинами можем записать

. (6.2)

Для однородного электрического поля связь между напряженностью   и напряжением U дается выражением  , где d — в данном случае расстояние между пластинами, U — напряжение на конденсаторе.    Из выражений (6.1), (6.2) и (5.11) получаем

. (6.3)

Электроемкость конденсатора прямо пропорциональна площади обкладок и обратно пропорциональна расстоянию между обкладками.    При введении диэлектрика между обкладками конденсатора его электроемкость увеличивается в   раз:

. (6.4)

Энергия заряженного конденсатора. 

Если на обкладках конденсатора электроемкостью C находятся электрические заряды + q и - q, то согласно формуле (42.1) напряжение между обкладками конденсатора равно

 . (6.5)

В процессе разрядки конденсатора напряжение между его обкладками убывает прямо пропорционально заряду q от первоначального значения U до 0. Среднее значение напряжения в процессе разрядки равно

 . (6.6)

Для работы А, совершаемой электрическим полем при разрядке конденсатора, будем иметь:

. (6.7)

Следовательно, потенциальная энергия W_p конденсатора электроемкостью C, заряженного до напряжения U, равна

. (6.8)

Энергия конденсатора обусловлена тем, что электрическое поле между его обкладками обладает энергией. Напряженность E поля пропорциональна напряжению U, поэтому энергия электрического поля пропорциональна квадрату его напряженности.

Плоский конденсатор состоит из двух параллельных металлических пластин площадью S каждая, расположенных на близком расстоянии d друг от друга и несущих заряды +Q и – Q. Если линейные размеры пластин велики по сравнению с расстоянием d, то электрическое поле между пластинами можно считать эквивалентным полю между двумя бесконечными плоскостями, заряженными разноимённо. Силовые линии поля параллельны друг другу и перпендикулярны пластинам.

Основной характеристикой конденсатора является его емкость – величина, пропорциональная заряду q и обратно пропорциональная напряжению между обкладками:

(1)

Разность потенциалов

(2)

где U – напряжение между обкладками.

Энергией заряженного конденсатора W называется полная энергия системы двух проводников и вычисляется по формуле:

(3)

Влетая в плоский конденсатор, частица движется криволинейно, т.к. на нее действует электрическая сила:

, (4)

направленная противоположно линий напряжённости электрического поля (т.е. противоположно направлению оси Оу) и сила тяжести:

, (5)

направленная вертикально вниз (т.е. противоположно направлению оси Оу).

Равнодействующая этих сил направлена вдоль оси Оу и равна:

(6)

Проекции равнодействующей силы на оси координат:

(7)

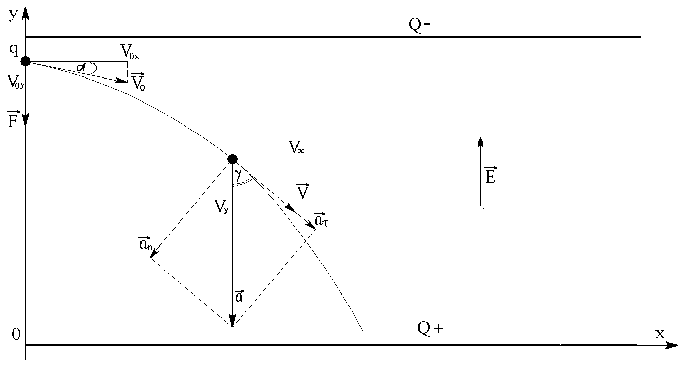
Рис 2.

При неравномерном движении частицы по криволинейной траектории ускорение можно разложить на два слагаемых. Одно из них коллинеарно скорости и, следовательно, направлено по касатель­ной к траектории. Поэтому его называют тангенциальным (т. е. касательным) ускорением и обозначают а_ . Второе слагаемое является нор­мальным ускорением, которое направлено к центру описываемой электроном кривой; определяется формулой .

Итак, , первое слагаемое характеризует быстроту изменения модуля скорости, второе слагае­мое – быстроту изменения направления скорости.

Составляющие а_ и а_п перпендикулярны друг к другу. Поэтому квадрат модуля ускорения равен сум­ме квадратов модулей составляющих: Отсюда следует, что:

(8)