21. Структурные средние. Общая характеристика, анализ и интерпретация.

Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены ,в основном, модой и медианой.

Мода — это наиболее часто встречающийся вариант ряда. Мода применяется, например, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта, обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда необходимо сначала определить модальный интервал (по максимальной частоте), а затем — значение модальной величины признака по формуле:

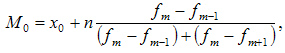
где:

•  — значение моды

•  — нижняя граница модального интервала

•  — величина интервала

•  — частота модального интервала

•  — частота интервала, предшествующего модальному

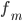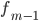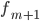•  — частота интервала, следующего за модальным

Медиана — это значение признака, которое лежит в основе ранжированного ряда и делит этот ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот   , а затем определяют, какое значение варианта приходится на нее. (Если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

М_е = (n_{(число признаков в совокупности)} + 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем — значение медианы по формуле:

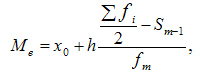
где:

•  — искомая медиана

•  — нижняя граница интервала, который содержит медиану

•  — величина интервала

•  — сумма частот или число членов ряда

•  - сумма накопленных частот интервалов, предшествующих медианному

•  — частота медианного интервала

Квартиль

Первый квартиль вычисляется по формуле:

– нижняя граница квартильного интервала,

– величина квартильного интервала,

– номер квартильного признака,

– сумма накопленных частот (весов) в интервалах, предшествующих

квартильному,

– частота квартильного интервала.

Аналогично рассчитывается третий квартиль. Второй же квартиль равен медиане.

Дециль

Рассчитывается по аналогии с расчетом квартиля. Можно найти девять децилей.

Средняя должна исчисляться не просто тогда, когда есть вариация признака, а

тогда, когда мы располагаем качественно однородным вариационным рядом. Среднюю

как обобщающую характеристику нельзя применять к таким совокупностям, отдельные

части которых подчиняются различным законам распределения (или) развития в

отношении величины распределяемого признака.

22.Понятие вариации и её значение в экономических исследованиях.

Вариация– это колеблемость значений признака у отдельных единиц совокупности.

Наличию вариации обязана своим появлением статистика. Большинство

статистических закономерностей проявляется через вариацию. Изучая вариацию

значений признака в сочетании с его частотными характеристиками, мы

обнаруживаем закономерности распределения (например: население по возрасту,

студентов по уровню оценок).

Рассматривая вариацию одного признака параллельно с изменением другого, мы

обнаруживаем взаимосвязи между этими признаками или их отсутствие (например:

зависимость между торговой площадью и товарооборотом).

Вариации в статистике проявляются двояко, либо через изменения значений

признака у отдельных единиц совокупности, либо через наличие или отсутствие

изучаемого признака у отдельных единиц совокупности.

Изучение вариации в статистике имеет как самостоятельную цель, так и является

промежуточным этапом более сложных статистических исследований.