5. Выявление основной тенденции развития динамических рядов.

Рассматривая массовые показатели в динамике, можно проследить тенденцию их изменения. Эта закономерность, заложенная в социально – экономическом явлении, называется трендом или основной тенденцией развития.

В социально – экономических рядах динамики можно наблюдать тенденции трех видов:

- среднего уровня;

- дисперсии;

- автокорреляции.

Тенденция среднего уровня выражается с помощью математической функции, вокруг которой варьируют фактические уровни исследуемого явления. Часто тенденции среднего уровня называют детерминированной (неслучайной) составляющей ряда динамики.

Тенденция дисперсии представляет собой тенденцию изменения отклонений между эмпирическими уровнями и детерминированной компонентой ряда.

Тенденция автокорреляции – это тенденция изменения связи между отдельными уровнями ряда динамики.

Тренд необходимо выявить, а затем рассчитать. А затем, предположив, что данная закономерность сохранится в будущем, можно построить прогноз.

Начальным этапом выделения и анализа тренда является проверка гипотезы о его существовании.

Существуют различные критерии проверки наличия тренда. Например, проверка существенности разности средних, метод Фостера – Стюарта и другие.

После установления наличия основной тенденции развития в ряду динамики, производится ее выявление с помощью методов выравнивания (сглаживания). К этим методам относятся следующие:

1. Графический метод или метод усреднения по левой и правой половине. При нем ряд динамики разделяют на две части, находят для каждой из них среднее арифметическое значение и проводят через полученные точки линию тренда на графике.

2. Метод укрупнения интервалов основан на укрупнении периодов времени, к которым относятся уровни ряда. При этом методе ряд динамики делят на некоторое достаточно большое число интервалов.

Если интервальные средние уровни не позволяют увидеть тенденцию, то увеличивают размах интервалов, уменьшая одновременно их число.

3. Метод простой скользящей средней заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда. Затем средний уровень из такого же числа уровней, начиная со второго, далее – с третьего и т.д.

Суть метода состоит в том, что данный метод позволяет сглаживать случайные колебания в уровнях развития явления во времени.

Период осреднения выбирается равным временному интервалу, в течение которого начинается и заканчивается цикл развития какого – либо явления. Исходные данные разбивают на группы (3, 4, 5), а затем просчитывают скользящие средние по формулам. При этом первый показатель отбрасывается, последний добавляется.

Формулы для расчета трехлетней скользящей средней:

4. Метод взвешенной скользящей средней. Его отличие от предыдущего метода состоит в том, что уровни, входящие в интервал, суммируются с различными весами.

i – порядковый номер уровня интервала сглаживания.

Для отображения основной тенденции развития социально – экономических явлений применяются полиномы различной степени, экспоненты, логистические кривые и другие функции.

- полином первой степени;

- полином второй степени;

- полином третьей степени;

- полином n-ной степени;

Если тренд выявлен, то приступают к его расчету. Для этого рассматривают, какой математической функцией можно описать фактические данные. Если эта функция известна, то ее рассчитывают, если неизвестна, то рассчитывают 4 или 5 предполагаемых, а затем по наименьшему значению ошибки аппроксимации выбирается функция.

Техника выравнивания по прямой имеет наиболее простое выражение.

Рассмотрим уравнение прямой:

Для определения значения у необходимо рассчитать и . Для этого рассчитывается система уравнений с применением способа условного нуля.

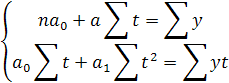
Если значений у четное количество, то два средних по времени обозначается через (-1) и (+1), а остальные показатели по нечетному ряду соответственно со знаком «−» или «+».

Если имеется нечетное количество показателей, то средний по времени обозначается через ноль, а остальные соответственно со знаком «−» или «+» подряд.

Рассчитав коэффициенты и и подставив их в уравнение, находим значение у для данного периода времени, а затем, предположив что данная тенденция сохраняется в будущем, строится прогноз.