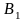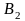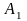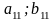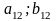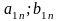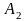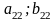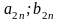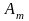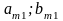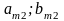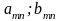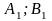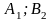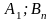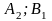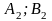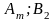- •1.Задачи теории игр в экономике, финансах и бизнесе.
- •Антагонистические
- •Игры с природой
- •Неантагонистические
- •2. Основные понятия и определения антагонистических игр.
- •3.Функция выигрыша и матрица выигрышей. Чистые стратегии игроков. Принцип доминирования стратегий. Соотношение между матрицами выигрышей игроков а и в в парной антагонистической игре с нулевой суммой.
- •4. Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий.
- •5. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Соотношение между ними.
- •6.Критерий решения игры в чистых стратегиях.
- •7.Доказательство утверждения .
- •8.Теорема об удовлетворительности игровой ситуации для игрока a.
- •9. Теорема об удовлетворительности игровой ситуации для игрока b
- •10. Равновесие в антагонистической игре.
- •11. Смешанные стратегии. Функция выигрыша и цена игры в смешанных стратегиях.
- •12.Теорема о существовании показателей эффективности и неэффективности смешанных стратегий в антагонистической игре.
- •13. Теорема о существовании нижней и верхней цен игры в смешанных стратегиях.
- •16.Аналитическое решение игры 2×2 в смешанных стратегиях.
- •Рассмотрим игру 2х2.
- •Для того, чтобы их найти, воспользуемся теоремой об активных стратегиях.
- •Пусть игра задана матрицей
- •Д ля второго игрока
- •19.Геометрический метод нахождения цены игры 2×n и оптимальных стратегий игрока a.
- •20. Геометрический метод нахождения цены игры m×2 и оптимальных стратегий игрока b.
- •2)В общем случае схема решения игры 2xn или nx2 графическим методом состоит в следующем.
- •21.Доминирование смешанных стратегий для игрока a.
- •22.Доминирование смешанных стратегий для игрока b.
- •23. Решение матричной игры m×n сведением к задаче линейного программирования для игрока a.
- •24. Решение матричной игры m×n сведением к задаче линейного программирования для игрока b.
- •25. Основные понятия и определения теории игр с природой.
- •26. Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределённости.
- •27. Критерий Байеса оптимальности чистых стратегий относительно выигрышей.
- •30. Критерий Лапласа оптимальности чистых стратегий относительно рисков.
- •31.Критерий (крайнего пессимизма) Вальда оптимальности чистых стратегий.
- •32.Максимаксный критерий (крайнего оптимизма) оптимальности чистых стратегий.
- •33.Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
- •34.Определение показателей оптимизма и пессимизма игрока, принимающего решения по критерию Гурвица относительно выигрышей.
- •35.Учёт выигрышей по критерию Гурвица крайним пессимистом, крайним оптимистом и нейтралом.
- •36.Вероятностная интерпретация коэффициентов критерия Гурвица.
- •37.Критерий Севиджа
- •38.Миниминный критерий.
- •39.Критерий пессимизма – оптимизма Гурвица оптимальности чистых стратегий относительно рисков.
- •40. Критерий Гермейера оптимальности чистых стратегий
- •42.Основные понятия и определения в теории неантагонистических (бескоалиционных) игр. Способы задания неантагонистической игры.
- •43.Стратегическая форма игры. Чистые и смешанные стратегии игроков в неантагонистических (бескоалиционных) играх. Доминирование стратегий.
- •Семейная пара принимает решение о месте куда они могут пойти в свободное время. Так он предлагает футбол, а она балет
- •45. Равновесие по Нэшу в смешанных стратегиях.
- •46. Аналитическое решение биматричных игр 2×2.
- •Рассмотрим случай, когда матрица [2x2]-не имеет седловой точки.
- •А цена игры (в смешанных стратегиях) V определяется формулой
- •Аналогичный анализ можно провести для второго игрока.
- •47. Геометрическое решение биматричных игр 2×2
- •48. Модель дуополии по Курно.
- •49. Модель дуополии по Бертрану.
- •50. Модель «Проблема общего».
- •51. Оптимальность по Парето в неантагонистических (бескоалиционных) играх.
- •52. Позиционная форма игры.
- •53. Понятие о конечных играх с совершенной информацией.
- •54. Стратегическая форма позиционной игры с совершенной информацией.
- •55. Равновесие по Нэшу в позиционной игре с совершенной информацией.
- •56. Обратная индукция и позиционные игры с совершенной информацией.
- •57. Модель дуополии по Штакельбергу.
- •58. Модель последовательного торга.
- •59. Модель «инвесторы и банк».
1.Задачи теории игр в экономике, финансах и бизнесе.
Теория игр – раздел современной математики, изучающий математические модели принятия решений в т.н. конфликтных ситуациях.
Математическая модель – это математическое описание компонентов и функций, отображающих существенные свойства моделируемого объекта.
Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения.
Игроки – заинтересованные в конфликте стороны.
Стратегия – любое возможное действие игрока.
Игровая ситуация – результат выбора каждым из игроков своей стратегии.
Выигрыш – то, что обуславливает интерес игроков. (похвала, порицание, приз, штраф).
Три вида игр:
Антагонистические
Страховщик и страхователь
На рынке есть страховщик и страхователь. Эта игра антагонистическая, так как выигрыш одного игрока равен проигрышу другого.
Взаимодействие этих сторон можно рассматривать, как игру, потому что есть конфликт интересов. У каждого игрока есть свои стратегии. И они нацелены на максимизацию своего выигрыша, либо минимизацию проигрыша.
Игры с природой
Предположим, что инвестор может купить акции одной из 3 компаний. Роль природы исполняет ситуация на фондовом рынке, которая в разные периоды складывается по-разному. Инвестору надлежит принять решение в условиях неопределенности, какой компании отдать предпочтение. На основе этих составляются матрицы выигрышей.
Неантагонистические
На рынке есть две фирмы А и В, производят аналогичные товары. Они выбирают объем производимых товаров Q1 и Q2.
Если Q=0, то P=A
При этом издержки у них одинаковы = C
Цена зависит от Q: P(Q)=A-Q
Чем больше Q, тем меньше P.
Pk=(A-Q-C)*Qk
Задача этой модели, найти равновесные Q1* и Q2*, которые создают ситуацию, которая является равновесием Нэша.
Необходимо найти:
P1(Q1;Q2*) -> max
P2(Q1*;Q2) -> max
2. Основные понятия и определения антагонистических игр.
Стратегия – любое возможное действие игрока. Множество стратегий – все возможные стратегии игроков
Игровая
ситуация
– результат выбора каждым из игроков
своей стратегии.

Множество
игровых ситуаций
– все возможные варианты игровых
ситуаций. Образует ситуационное
пространство игры.
Игра – упрощенная, формализованная модель конфликта. Важным отличием игры от реального конфликта является наличие жёстко определённых правил поведения.
Игроки – заинтересованные в конфликте стороны.
Платежная матрица – матрица, элементами корой являются выигрыши (проигрыши) игрока.
Антагонистическая игра – игра с нулевой суммой, в которой выигрыш одного игрока равен проигрышу другого.
FA=-FB , где F – функция выигрыша.
Платежная матрица:
Стратегии игрока A |
Стратегии игрока B |
|||
|
|
… |
|
|
|
|
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
… |
|
|
|
… |
|
Матрица игровых ситуаций:
Стратегии игрока A |
Стратегии игрока B |
|||
|
|
… |
|
|
|
|
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
… |
|
|
|
… |
|
Взаимосвязь заключается в том, что при игровой ситуации (A1;B1) игроки соответственно достигают выигрышей(проигрышей) (a11;b11)