№ 12. Неметрологические характеристики си

Они определяют возможности и ограничения практической эксплуатации СИ, т.е. использования по назначению этих средств, их транспортирования, хранения, технического облуживания и ремонта.

Надежность СИ – способность сохранять заданные характеристики в установленных пределах при определенных условиях в течение заданного времени.

Включает в себя показатели:

— безотказности (вероятность безотказной работы, средняя наработка до отказа, интенсивность отказов и наработка на отказ).

— долговечности (оптимальное время эксплуатации, предельное время эксплуатации, гарантийный срок службы).

— ремонтопригодности (вероятность восстановления за заданное время и среднее время восстановления).

— сохраняемости (среднее время сохраняемости, вероятность сохранения работоспособности).

А также масса, габариты, вид и напряжение источника тока, потребляемая мощность, устойчивость к климатическим условиям и механическим воздействиям, время установления рабочего режима и другие.

№ 13. Классы точности средств измерения

Класс точности представляет собой обобщенную характеристику средств измерений, отражающую уровень их точности и представленную набором нормируемых метрологических характеристик.

Пределы допускаемой абсолютной основной погрешности выражают значением.

или

Пределы допускаемой приведенной основной погрешности.

где р – отвлеченное положительное число, выбираемое из ряда ; ; .

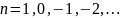
Пределы допускаемой относительной погрешности.

№ 14. Распределение вероятностей дискретной и непрерывной случайной величины

Дискретная случайная величина может принимать лишь счетное множество значений 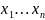с вероятностями 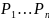. При этом все возможные значения случайно величины образуют полную группу событий, для которых

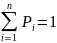
Наиболее полной характеристикой дискретной величины является ее распределение вероятностей. Оно представляет собой пересечения всех возможных значений случайной величины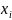 с указанием вероятностей 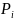этих значений.

Непрерывная случайная величина может принимать любое значение из конечного или бесконечного интервала. Поскольку значения могут отличаться друг от друга на сколь угодно малую величину, то вероятность каждого из них также бесконечно мала.

При изучении непрерывных случайных величин в качестве события, вероятность которого в общем случае отлична от нуля, рассматривают вероятность попадания случайной величины X в элементарный интервал x, x+dx. Вероятность такого события:

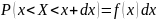
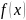- функция значений случайной величины, называемая плотностью вероятности.

На практике для выявления распределения вероятностей рассматривают некоторое множество интервалов 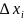в диапазоне возможных значений в каждый из этих интервалов. Расположив значения в порядке возрастания и обозначив соответствующие вероятности, получим ступенчатую кривую — гистограмму.

При гистограмма переходит в плавную кривую распределения плотности вероятности непрерывной величины X. Соответствующее уравнение называет законом распределения.