№ 4. Измерение как информационный процесс

Измерения обеспечивают получение информации о значениях измеряемой физической величины – измерительной информации, и, следовательно, увеличивают наши знания (уменьшают их неопределенность) о количественных характеристиках свойств объектов.

Понятие информации имеет обобщенный философский смысл и отражает одно из объективных свойств материального мира. Не случайно основная ее идея заключается в том, что с информацией можно обращаться также, как с такими физическими величинами, как масса и энергия. Здесь имеется в виду, что информацию, как и энергию, можно извлекать, передавать, преобразовывать к виду, удобному для использования.

Количество информации в сообщении, которое содержит сведения об объекте, определяется величиной, обратной вероятности сообщения и вычисленной в логарифмических единицах:

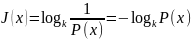
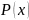- вероятность сообщения.

Оценку информационных свойств сообщения в целом осуществляют с помощью специальной характеристики, которая называется энтропия H. Она характеризует среднее количество информации, приходящее на одно сообщение.

В общем случае для N разных событий, характеризующихся своими вероятностями и определенным количеством информации о каждом из них, для определения количества информации, которое содержится в единичном сообщении, нужно найти математическое ожидание количества информации о каждом из событии или провести усреднение с учетом P(x):

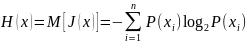
Энтропия источника измеряется в двоичных единицах или в битах на сообщение.

№ 5. Количественное оценивание физических величин с использованием эмпирических шкал

Основная задача измерения – формирование некоторого объективного заключения о свойствах и состоянии наблюдаемого фрагмента действительности.

Наблюдение – представляет собой наиболее элементарный метод эмпирического познания, позволяющий получить некоторую первичную информацию об объектах окружающий действительности и являющийся необходимым элементом измерения и эксперимента.

Результатом наблюдения являются оценки, выражаемые с помощью качественных и сравнительных понятии, в то время как результаты измерений – это всегда числовые величины, отражающие свойства реальных объектов.

Эмпирическая шкала – классификация изучаемых свойств, последовательно упорядоченных, каждый класс которого будет отличаться степенью интенсивности интересующего свойства.

Сначала рассматриваются качественные оценки, затем – количественные. Такие эмпирические шкалы называются порядковыми (шкала Мооса, шкала М.М. Протодьяконова).

Каждая эмпирическая шкала отражает уровень знания соответствующий моменту своего создания и предназначена для удовлетворения конкретных практических нужд. Применение эмпирических шкал продиктовано соображениями удобства, экономичности и достаточной для практических целей точности и информативности.

Что касается установления числового соотношения между свойствами объектов с помощью эмпирических шкал, то этот процесс не отражает технических, метрологических и гносеологических аспектов измерений, потому должен быть отнесен к количественному оцениванию.

По мере развития науки и техники, физические величины могут переходить из разряда оцениваемых в разряд измеряемых.