№ 45. Интерполяция, аппроксимация и экстраполяция экспериментальных данных

Задачу, связанную с определением указанного математического выражения, принято называть аппроксимацией.

А также, если мало, смотри № 23.

Интерполяция — в вычислительной математике способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений.

Многим из тех, кто сталкивается с научными и инженерными расчётами часто приходится оперировать наборами значений, полученных опытным путём или методом случайной выборки. Как правило, на основании этих наборов требуется построить функцию, на которую могли бы с высокой точностью попадать другие получаемые значения. Такая задача называется аппроксимацией. Интерполяцией называют такую разновидность аппроксимации, при которой кривая построенной функции проходит точно через имеющиеся точки данных.

Экстраполяция — особый тип аппроксимации, при котором функция аппроксимируется вне заданного интервала, а не между заданными значениями.

№ 46. Проверка гипотезы о равенстве средних значений двух нормально распределенных совокупностей с использованием параметрических критериев

Смотри № 20.

№ 47. Критерии согласия. Проверка гипотезы о законе распределения с использованием критерия Колмогорова-Смирнова

Смотри № 21.

Рассмотренный критерий относится к группе так называемых критериев согласия, обеспечивающих объективную оценку близости фактических и теоретических распределений. К этой группе относится и критерий Колмогорова-Смирнова.

Очевидное преимущество этого критерия – простота. Критерий согласия может быть использован также для проверки гипотезы о принадлежности двух выборок Х и У, объемами и 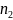соответственно, к одной генеральной совокупности.

№ 48. Статистическая проверка гипотез. Ошибки первого и второго рода. Проверка гипотезы против альтернативы

Смотри № 20.

Проверка гипотезы против альтернативы.

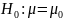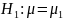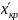Пусть проверяется гипотеза против альтернативы . Приняв в качестве критерия проверки выборочную среднюю, легко построить законы распределения этого критерия как при . Выбрав , теперь легко найти вероятности ошибок как первого, так и второго рода:

Существенно, что изменением невозможно добиться одновременного уменьшения вероятностей ошибок первого и второго рода. Уменьшить одну из них можно лишь за счет увеличения другой. Но, во всяком случае, проверка гипотезы против альтернативы позволяет оценивать надежность как принятия нулевой гипотезы, так и ее отклонения.

Проверка гипотезы против альтернативы дает более надежные результаты, чем проверка против простой конкурирующей гипотезы. Однако возможность такого подхода ограничена, так как далеко не для всякой гипотезы удается сформулировать альтернативу.

№ 49. Прямые, косвенные, совместные и совокупные измерения. Определения, характеристика и особенности этих видов измерения.

Прямое измерение – измерение, при котором искомое значение физической величины находят непосредственно из опытных данных.

Косвенное измерение – значение искомой величины определяют на основе известной математической зависимости.

Совокупные измерения – неоднократные, обычно прямые измерения одной или нескольких одноименных величин с получением искомого результата путем решения системы уравнений, составляемых по частным результатам измерений.

Совместные измерения – это проводимые одновременно измерения двух или нескольких неодноименных величин с последующим вычислением искомого результата на основе зависимостей, связывающей его с указанными величинами.

№ 50. Теория единства измерений. Основные положения, принципы. Понятие «испытание» и «контроль» и их отличие от измерения

№ 51. Обработка результатов линейных и нелинейных измерений

№ 52. Хранение и воспроизведение единиц физических величин. Эталоны единиц физических величин. Классификация поверочных схем (методов). Общий алгоритм процедуры поверки

Эталон единицы физической величины представляет собой средство (или комплекс средств) измерений наивысшей точности, обеспечивающее воспроизведение и (или) хранение единицы для передачи ее размера низшим по точности СИ.

Предполагается, что любое СИ должно быть предварительно поверено, т.е. должно быть определено соответствие точностных характеристик этого СИ регламентированным значениям и пригодность его к применению. Однако непосредственно перед экспериментом даже поверенное СИ необходимо опробовать. Под опробованием понимают цикл операций, позволяющих определить потенциальную работоспособность СИ и выявить возможные дефекты в его функционировании, возникшие в послеповерочный период.