№ 35. Обработка результатов прямых многократных измерений с нормальным распределением данных

Пусть имеются полученные экспериментально нормально распределенные данные , отражающие результаты прямых наблюдений, из которых исключены грубые и систематические погрешности.

Методика обработки этих данных сводится к следующему:

1. Находят наиболее вероятное значение искомого результата, которым является среднее арифметическое выборки, определяемое по формуле:

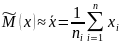
2. Оценивают случайное рассеяние экспериментальных данных путем вычисления среднеквадратического отклонения (СКО) S по формулам:

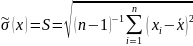
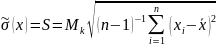
3. Вычисляют СКО результата измерений:

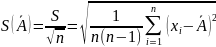
4. Определяют доверительные границы случайной составляющей погрешности результата измерения. Эти границы определены по формуле:

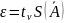
5. Определяют доверительную границу неисключенных остатков систематической составляющей погрешности результата измерения. Затем выявляют доверительные границы по формуле:

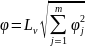
6. Определяют доверительную границу общей погрешности результата измерений. Для этого оценивают соотношение между и 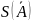и, в зависимости от этого соотношения определяют величину .

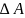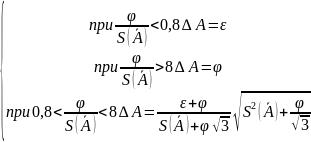
7. Окончательный результат записывают в виде: .

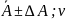№ 36. Обработка результатов косвенных измерений

При косвенных измерениях определение искомой величины А осуществуляется на основе известной функции, связывающей эту величину с аргументами а:

Описываемая ниже методика обработки справедлива при условии отсутствия корреляции между результатами наблюдений каждой пары входящих в аргументов. Проверка этого условия предполагает:

1. Вычисление коэффициента корреляции.

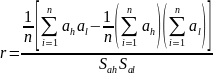
2. Вычисление показателя корреляции по формуле:

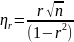
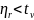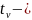3. Проверку выполнения неравенства: где коэффициент доверия.

Среднее значение результата косвенного измерения получают простой подстановкой в уравнение (*) средних значений результатов прямых измерений аргументов:

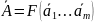
Поскольку в общем случае функциональная зависимость (*) является нелинейной, то дальнейшую обработку косвенных измерений осуществляют с использованием метода линеаризации. Этот метод предполагает разложение указанной зависимости в ряд Тейлора, ограниченный членами, содержащими только первые производные.

№ 37. Формы представления результатов эксперимента, направленного на установление значения конкурентного параметра измеряемой физической величины

Формы представления результатов эксперимента определяются назначением и характером их использования.

Результаты осуществляются по следующим правилам:

1. Результат измерения выражают именованным или неименованным числом.

2. Указанный результат дополняют характеристиками его погрешности или статистическими оценками этих характеристик.

3. В качестве характеристик погрешности измерений используют:

— средние квадратические отклонения (СКО) погрешности или границы, в которых она находится с заданной вероятностью.

— характеристики случайной составляющей погрешности.

— характеристики неисключенной систематической составляющей погрешности.

4. В качестве статистических оценок характеристик погрешности результата измерений используют оценки и границы их доверительных интервалов.

5. Допускается не указывать характеристики погрешности, если результат измерений получен по стандартизированной или аттестованной МВИ.

6. Результат измерений допускается представить доверительным интервалом, покрывающим истинное значение измеряемой величины с известной доверительной вероятностью.

7. Результаты измерений при необходимости дополняют сведениями: о методике, по которой они были получены, условиях проведения эксперимента, модели объекта измерений и ее параметрах, принятых в качетве измеряемых величии и др.

8. Числа, отражающие окончательный результат округляются в соответствии со следующими правилами:

— количество значащих цифр при указании погрешности не должно превышать двух.

— число, выражающее результат измерений, должно оканчиваться цифрой того же разряда, что и значение его погрешности.

— если в числе, выражающем результат измерения, первая из заменяемых нулями или отбрасываемых цифр больше или равно 5, но за ней следуют отличные от нуля цифры, то последнюю оставшуюся цифру увеличивают на единицу.

— если характеристики погрешности измерений определяли в ходе самих измерении, то результат последних должен сопровождаться статистическими оценками характеристик погрешности.

— округление следует проводить только в окончательном результате, осуществляя промежуточные вычисления с числами, содержащими не менее одного лишнего знака.

Табличная форма представления обеспечивает:

— возможность сведения воедино и исходных данных измерений, и результатов различных этапов их обработки.

— удобство упорядочивания данных по возрастанию или убыванию.

— возможность отображения данных компактно и практически с любой степенью точности.

— удобство использования полученных результатов эксперимента для дальнейшей обработки, связанной с так называемым табличным дифференцированием, интегрированием интерполированием и сглаживанием.

— табличная форма часто позволяет установить определенные закономерности исследуемых процессов и явлений.

Графическая форма представления результатов измерительного эксперимента наиболее распространена, что связано прежде всего с ее наглядностью.

К недостаткам можно отнести громоздкость изображения функций с большим числом переменных и относительно малая точность.

Графики представляют собой диаграммы, отражающие количественные зависимости различных параметров. Различают два вида графиков – статистические и функциональные.

Аналитическая форма представления экспериментальных данных отличается компактностью и обеспечивает удобство проведения расчетов на ЭВМ, а также аналитических исследований, полученных зависимостей.

Кроме того, при использовании формул отпадает необходимость интерполяции. В то же время с помощью формул получают обычно более грубые значения функции, чем по таблицам и графикам, при их использовании обязательно должны выполняться расчеты и требуются дополнительные указания соответствующих пределов применимости.

№ 38. Представление результатов измерительного эксперимента, направленного на установление зависимостей между фактором и откликом.

Смотри № 37.

№ 39. Методы исключения (уменьшения) случайных, систематических и грубых погрешностей

1. Случайные погрешности.

Случайные погрешности формируются под влиянием многочисленных факторов, учет которых практически неосуществим, поэтому исключить эти погрешности из результатов измерения невозможно.

2. Исключение систематической погрешности.

Осуществляют в тех случаях, когда на более ранних стадиях измерительного процесса указанные погрешности не удалось уменьшить до уровня незначительных случайных составляющих. Поскольку случайная составляющая измерения определяется значением , то при известной малой величине этого значения, требование к величине неисключенного остатка систематической погрешности можно записать в виде:

3. Грубые погрешности можно рассматривать как результаты наблюдений, не принадлежащие исследуемой генеральной совокупности и, следовательно, они должны быть исключены из дальнейшей статистической обработки. Соответствующая операция получила название цензурирования выборки.

Наиболее наглядный способ цензурирования предполагает построение гистограмм распределения результатов наблюдений. При этом, если часть экспериментальных данных будет иметь отличное от остальных распределение, то, ясно, что она не принадлежит генеральной совокупности наблюдения.

Правило трех сигм: отклонение истинного значения измеряемой величины от среднего арифметического результата измерений не превосходит утроенной средней квадратической ошибки этого среднего значения.

Основываясь на этом правиле, можно сформулировать простейший способ выявления промахов. Из анализируемой выборки удаляют сомнительные отсчеты. Затем по оставшимся в выборке данным вычисляют эмпирический стандарт S и все значения для которых признают промахами, исключая их из дальнейшей выборки.

Еще один способ обнаружения результатов наблюдений, содержащих грубые погрешности, заключается в следующем. Все полученные результаты представляют в виде упорядоченного ряда . Если крайние члены, являющиеся наибольшим и наименьшим результатами, значительно отстоят от ближайших членов, то это дает основание для проверки их на наличие грубых погрешностей. Такую проверку осуществляют на основе сравнения сомнительного (выскакивающего) значения с остальными результатами наблюдений. Для этого вычисляют дробь:

– среднее арифметическое и СКО экспериментальных данных.

Затем задают уровень значимости , т.е. вероятность того, что сомнительный результат действительно мог иметь место в данной совокупности результатов измерений. выбирают из ряда 1, 2, 5, 10%. Далее сравнивают вычисленное значение с теоретическим значением -процентной точки наибольшего по абсолютному значению нормированного выборочного отклонения.

Если при числе n измерений , то экспериментальное данное подлежит исключению, как содержащее грубую погрешность.