№ 21. Проверка гипотезы о законе распределения с использованием критерия Пирсона

Пусть имеется выборка достаточно большого объема (n 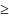50). Разделим всю область, куда попадают выборочные значения на конечное число интервалов, в каждый из которых должно попасть несколько выборочных значений. Если в некоторых интервалах таких значений окажется мало (< 5), то эти интервалы объединяют с соседними.

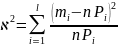
m_i – число элементов выборки, попавших в i-й интервал.

P_i – вероятность попадания случайно величины x в i-й интервал в случае справедливости приписываемого ей закона распределения.

Величина хи-квадрат является случайной, так как при разных выборках они принимает разные значения. Ясно, что чем меньше отличаются друг от друга m_i и nP_i, тем меньше хи-квадрат. Следовательно, этот критерий в известной степени характеризует степень близости фактического и предполагаемого распределения.

Можно показать, что, если проверяемая гипотеза верна, то при распределение критерия стремится к распределению хи-квадрат с k – 1 степенями свободы независимо от предполагаемого распределения случайной величины x. Именно поэтому этот критерий и получил наименование хи-квадрат.

Так как малые значения хи-квадрат соответствуют хорошему совпадению предполагаемого и фактического распределений, выберем правостороннюю критическую область из условия:

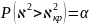
- вероятность ошибки первого рода.

Если хи-квадрат попадает в критическую область, то выдвинутая гипотеза отвергается.

Если в доверительную, то данные не противоречат гипотезе.

Вероятность попадания случайной величины в интервал 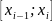при нормальном законе распределения вычисляют с использованием интеграла вероятностей Ф по формуле:

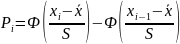
№ 22. Проверка гипотез с использованием непараметрических критериев

Подход не требует знания законов и параметров распределения, используют непараметрические критерии, которые выявляют путем выявления упорядоченности численных значений, полученных в результате наблюдений и установления между ними соответствий вид > или <.

Использование непараметрических критериев рассмотрим на примере критерия Вилкоксона применительно к задаче проверки гипотезы о принадлежности двух выборок к одной генеральной совокупности.

Пусть имеются две выборки элементы каждой из которых расположены по возрастанию.

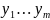
1. Объединяют все элементы двух выборок в упорядоченную последовательность объемом .

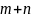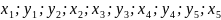
2. Определим число инверсий U в выражении.

Инверсия – каждая пара значений 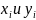для которых, 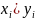иначе говоря число инверсий равно сумме чисел всех 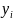стоящий впереди каждого .

3. Будем считать, что число инверсий подчиняется нормальному закону со средним 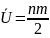и дисперсией .

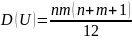4. Если гипотеза верна, то U полученное экспериментально (по выборке) не должно сильно отличаться от .

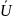Если 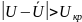, то гипотезу отвергают.

5. Критическое значение числа инверсий 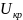при малых значениях m и n (< 14) для заданного уровня значимости табулированно.

Для больших значений m и n:

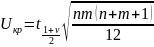
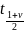– квантиль (0,1)-нормального распределения порядка .

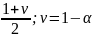В практике экспериментальных ислледований часто возникает задача проверки гипотезы о том, что расположение элементов двух видов (0 и 1) носит случайный характер, т.е. является стохастически независимым. Просто решить эту задачу с помощью метода серий.

20 образцов горных пород, пренадлежащих к одной генеральной совокупности, были разделены на две равные группы. Одну подвергли механическому воздействию, а другую нет.

1 — 5,22 5,3 5,4 5,32 5,1 5,2 5,34 5,6 5,5 5,27

2 — 5,7 5,41 5,28 5,38 5,15 5,8 5,42 5,65 5,31 5,14

5,1(0) 5,14(1) 5,15(1) 5,2(0) 5,22(0) 5,27(0) 5,28(1) 5,29(0) 5,3(0) 5,31(1) 5,32(0) 5,38(1) 5,4(0) 5,41(1) 5,42(1) 5,5(0) 5,6(0) 5,65(1) 5,7(1) 5,8(1)

Элементы 0 и 1 в скобках рядом с числовыми значениями последовательности означают принадлежность соответственно к 1 и 2 группам. Выпишем их:

01100010010101100111 (*)

Серия – подряд идущие элементы одного типа. Здесь серий 12.

То есть 0 – первая серия, 11 – вторая и так далее.

Можно показать, что, если число элементов в последовательности (*) достаточно велико (n>10), то распределение числа серий близко к нормальному с характеристиками:

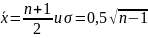
С вероятность 99,7% теоретическое число серий должно укладываться в интервал:

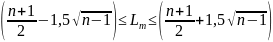
Для нашего примера при n=20 условие имеет вид:

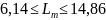
Так как 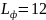укладывается в границы 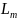, то можно сделать вывод о случайности расположения элементов в последовательности (*). Иначе говоря, последовательность измеренных значений признака носит случайный характер, и, следовательно, произведенное механическое воздействие не привело к значимым изменениям измеряемого признака.

Метод серий может быть использован также для проверки случайности последовательности изменения выборочных значений измеряемого признака. При этом определяют среднюю. Элементы, значения которых меньше средней, обозначают нулем, а элементы больше средней – единицей.