
- •11. Неравество и предельные значения
- •12.Первый замечательный предел
- •13.Второй замечательный предел
- •14.Понятие непрерывности функции
- •15.Арифметические операции над непрерывными функциями
- •16.Сложная функция и ее непрерывность
- •17.Понятие обратной функции
- •19.Понятие дифференцируемости и т.П.
- •20.Связь
- •22.Теорема о производной обратной функции
- •24.Логарифмическая производная
- •25.Таблица производных
- •26. Производные высших порядков
- •27. Теоремы о непрерывных функциях
- •28. Локальный max и min
- •18.Производная
- •31 .Условия монотонности функции на интервале
- •32. Достаточные условия локального экстремума
- •33. Отыскание точек локального экстремума.
26. Производные высших порядков
Пусть
функция
определена и дифференцируема на интервале
 .
Тогда ее производная
.
Тогда ее производная
 представляет собой функцию переменной
также определенную на интервале
.
в свою очередь может оказаться
дифференцируемой в некоторой точке
интервала
.
Производную от функции
называют второй производной (производной
второго порядка) от функции
и обозначают
представляет собой функцию переменной
также определенную на интервале
.
в свою очередь может оказаться
дифференцируемой в некоторой точке
интервала
.
Производную от функции
называют второй производной (производной
второго порядка) от функции
и обозначают
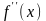 или
или
 .
Итак,
.
Итак,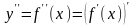 .
.
Далее
мы можем аналогично ввести понятие
третьей производной, как производной
от второй: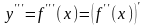 ,затем
четвертой и т. д.
,затем
четвертой и т. д.
27. Теоремы о непрерывных функциях
Теорема
(об устойчивости знака непрерывной
функции).
Если функция
непрерывна в точке
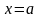 ,
и если
,
и если
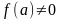 ,
то найдется такая
,
то найдется такая
 -окрестность
точки
,
что для всех значений аргумента из
указанной
-окрестности
функция
не обращается в нуль и имеет знак,
совпадающий со знаком
.Теорема
(о прохождении непрерывной функции
через нуль при смене знака).
Пусть функция
непрерывна на отрезке
и принимает на концах отрезка значения
разных знаков. Тогда внутри отрезка
найдется хотя бы одна точка
-окрестность
точки
,
что для всех значений аргумента из
указанной
-окрестности
функция
не обращается в нуль и имеет знак,
совпадающий со знаком
.Теорема
(о прохождении непрерывной функции
через нуль при смене знака).
Пусть функция
непрерывна на отрезке
и принимает на концах отрезка значения
разных знаков. Тогда внутри отрезка
найдется хотя бы одна точка
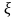 ,
в которой функция обращается в нуль
(
,
в которой функция обращается в нуль
(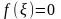 ).Теорема
(о прохождении непрерывной функции
через любое промежуточное значение).
Пусть функция
непрерывна на отрезке
,
причем
).Теорема
(о прохождении непрерывной функции
через любое промежуточное значение).
Пусть функция
непрерывна на отрезке
,
причем
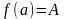 ,
,
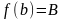 .
Пусть
.
Пусть
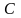 — любое число, заключенное между
и
— любое число, заключенное между
и
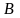 .
Тогда на отрезке
найдется точка
такая, что
.
Тогда на отрезке
найдется точка
такая, что
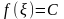 .Теорема
(Вейерштрасса) Если
функция
непрерывна на отрезке
,
то она ограничена на этом отрезке и
имеет на этом отрезке наибольшее и
наименьшее значение.
.Теорема
(Вейерштрасса) Если
функция
непрерывна на отрезке
,
то она ограничена на этом отрезке и
имеет на этом отрезке наибольшее и
наименьшее значение.
28. Локальный max и min
Локальный
максимум и локальный минимум объединяются
общим названием локальный
экстремум.
Если в некоторой окрестности точки
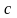 имеет место строгое неравенство
имеет место строгое неравенство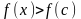 (
(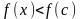 ),
то точка
называется точкой строгого локального
максимума (минимума).
Ферма (необходимое условие локального
экстремума дифференцируемой функции).
Если функция
дифференцируема в точке
и имеет в этой точке локальный экстремум,
то
),
то точка
называется точкой строгого локального
максимума (минимума).
Ферма (необходимое условие локального
экстремума дифференцируемой функции).
Если функция
дифференцируема в точке
и имеет в этой точке локальный экстремум,
то
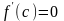 .Пусть
функция
определена всюду в некоторой окрестности
точки
.Пусть
функция
определена всюду в некоторой окрестности
точки
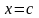 .
Точка
называется точкой
локального максимума,
если найдется
-окрестность
точки
,
в пределах которой значение
.
Точка
называется точкой
локального максимума,
если найдется
-окрестность
точки
,
в пределах которой значение
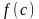 является наибольшим, то есть для любого
из интервала
является наибольшим, то есть для любого
из интервала
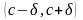 справедливо неравенство
справедливо неравенство
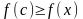 .
Точка
называется точкой локального
минимума,
если найдется
-окрестность
точки
,
в пределах которой значение
является наименьшим, то есть для любого
из интервала
справедливо неравенство
.
Точка
называется точкой локального
минимума,
если найдется
-окрестность
точки
,
в пределах которой значение
является наименьшим, то есть для любого
из интервала
справедливо неравенство
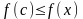 .
.
18.Производная
Производной функции в точке называется конечный предел (если он существует) при отношения приращения функции в этой точке к соответствующему приращению аргумента.
Производную
функции
в точке
будем обозначать символом
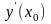 или
или
 .
.
Физический
смысл производной Рассмотрим
движение материальной точки по прямой
линии. Пусть
— это путь, пройденный точкой от начала
отсчета за время
,
а функция
описывает закон движения материальной
точки по прямой линии. Тогда
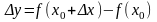 — это путь, пройденный точкой за
промежуток времени от
до
— это путь, пройденный точкой за
промежуток времени от
до
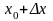 ,
а отношение
,
а отношение
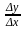 — средняя скорость движения на отрезке
— средняя скорость движения на отрезке
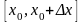 .
В таком случае предел отношения
при
,
равный
,
определяет мгновенную скорость точки
в момент времени
.
Производная
.
В таком случае предел отношения
при
,
равный
,
определяет мгновенную скорость точки
в момент времени
.
Производная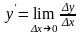 называется
предельными
издержками
производства. Аналогично можно определить
предельный
доход, предельную выручку, предельную
полезность и
так далее.
называется
предельными
издержками
производства. Аналогично можно определить
предельный
доход, предельную выручку, предельную
полезность и
так далее.
