
- •11. Неравество и предельные значения
- •12.Первый замечательный предел
- •13.Второй замечательный предел
- •14.Понятие непрерывности функции
- •15.Арифметические операции над непрерывными функциями
- •16.Сложная функция и ее непрерывность
- •17.Понятие обратной функции
- •19.Понятие дифференцируемости и т.П.
- •20.Связь
- •22.Теорема о производной обратной функции
- •24.Логарифмическая производная
- •25.Таблица производных
- •26. Производные высших порядков
- •27. Теоремы о непрерывных функциях
- •28. Локальный max и min
- •18.Производная
- •31 .Условия монотонности функции на интервале
- •32. Достаточные условия локального экстремума
- •33. Отыскание точек локального экстремума.
11. Неравество и предельные значения
При
определении предельного значения
тригонометрических функций в точке,
важную роль играет неравенство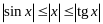 ,для
любого
,для
любого
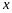 из интервала
из интервала
 справедливо.
справедливо.
Предельные значения тригонометрических функций
Докажем,
что предельное значение функции
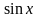 в точке
в точке
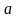 равно
равно
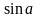 .
Рассмотрим функцию
.
Рассмотрим функцию
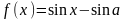 .
.
 Заметим,
что
Заметим,
что
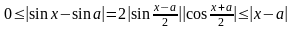 .Здесь
мы воспользовались неравенствами
.Здесь
мы воспользовались неравенствами
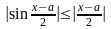 и
и
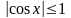 .
Поскольку
.
Поскольку
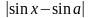 не меньше 0 и не больше
не меньше 0 и не больше
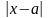 ,
а
,
а
 ,
то
является бесконечно малой функцией.
Следовательно,
,
то
является бесконечно малой функцией.
Следовательно,
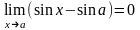 ,
а
,
а
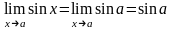 . Аналогично
можно доказать, что
. Аналогично
можно доказать, что
 .
Действительно, из неравенства
.
Действительно, из неравенства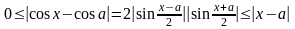 следует, что
следует, что
 .
.
12.Первый замечательный предел
Предельное
значение функции
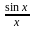 в точке
в точке
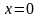 существует и равно единице:
существует и равно единице: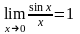 .
(2) Равенство (2) называют первым
замечательным пределом.
.
(2) Равенство (2) называют первым
замечательным пределом.
Следствия из первого замечательного предела
1)
 .2)
.2)
 3)
3)
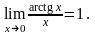
13.Второй замечательный предел
Предельное
значение функции
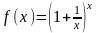 при
при
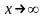 существует и равно
существует и равно
 :
: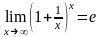 .Второй
замечательный предел также записывают
в виде
.Второй
замечательный предел также записывают
в виде
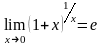 .
.
Следствия из второго замечательного предела
1)
 .2)
.2)
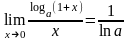 .3)
.3)
 .4)
.4)
 .
.
14.Понятие непрерывности функции
Функция
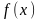 называется непрерывной
в точке
,
если предельное значение этой функции
в точке
существует и равно частному значению
называется непрерывной
в точке
,
если предельное значение этой функции
в точке
существует и равно частному значению
 ,
то есть, если
,
то есть, если
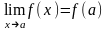 .
(1)Поскольку
.
(1)Поскольку
 ,
то равенство (1) можно представить в виде
,
то равенство (1) можно представить в виде
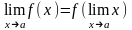 .
.
Следовательно, для непрерывной функции знак предела можно вносить под знак функции.
Точки, в которых функция не является непрерывной, называются точками разрыва функции.
Функция
называется непрерывной
на множестве
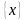 ,
если она непрерывна в каждой точке этого
множества. Классификация
точек разрыва :Устранимый разрыв.
Точка
называется точкой устранимого разрыва
функции
,
если предельное значение функции в этой
точке существует, но либо функция не
определена в этой точке, либо ее предельное
значение не равно частному значению
.Разрыв
первого рода.
Точка
называется точкой разрыва первого рода,
если в этой точке функция
имеет конечные, но не равные друг другу
правое и левое предельные значения:
,
если она непрерывна в каждой точке этого
множества. Классификация
точек разрыва :Устранимый разрыв.
Точка
называется точкой устранимого разрыва
функции
,
если предельное значение функции в этой
точке существует, но либо функция не
определена в этой точке, либо ее предельное
значение не равно частному значению
.Разрыв
первого рода.
Точка
называется точкой разрыва первого рода,
если в этой точке функция
имеет конечные, но не равные друг другу
правое и левое предельные значения: .
Разрыв
второго рода.
.
Разрыв
второго рода.
15.Арифметические операции над непрерывными функциями
Пусть
заданные на одном и том же множестве
функции
и
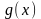 непрерывны в точке
.
Тогда функции
непрерывны в точке
.
Тогда функции
 ,
,
 ,
,
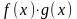 и
и
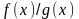 также непрерывны в точке
(частное при условии
также непрерывны в точке
(частное при условии
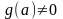 ).
).
16.Сложная функция и ее непрерывность
Последовательное
применение двух или нескольких функций
называется суперпозицией
этих
функций. Функции, образованные в
результате суперпозиции двух или
нескольких функций будем называть
сложными
функциями.
Например, сложная функция
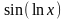 образована в результате суперпозиции
функций
образована в результате суперпозиции
функций
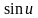 и
и
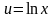 .Достаточно
определить сложную функцию, образованную
в результате суперпозиции двух функций.
Пусть функция
.Достаточно
определить сложную функцию, образованную
в результате суперпозиции двух функций.
Пусть функция
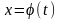 определена на некотором множестве
определена на некотором множестве
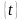 и пусть
— множество значений этой функции. Если
на указанном множестве
определена другая функция
и пусть
— множество значений этой функции. Если
на указанном множестве
определена другая функция
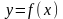 ,
то говорят, что на множестве
задана сложная функция переменной
,
то говорят, что на множестве
задана сложная функция переменной
 .
.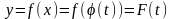 .Если
функция
непрерывна в точке
.Если
функция
непрерывна в точке
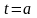 ,
а функция
непрерывна в точке
,
а функция
непрерывна в точке
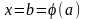 ,
соответствующей точке
,
то функция
,
соответствующей точке
,
то функция
 непрерывна в точке
.
непрерывна в точке
.
