1.Законы динамики. Основное уравнение динамики точки.

1-й закон динамики (закон инерции): всякое , изолированное от внешних воздействий тело , сохраняет состояние покоя или равномерного прямолинейного движения до тех пор , пока воздействие со стороны других тел не выведут его из этого состояния.

2-й закон динамики (основной): ускорение , сообщаемое м.т. силой , прямопропорционально величине этой силы и совпадает с ней по направлению. F=ma a=F/m

3-й закон динамики (закон взаимодействия): силы взаимодействия между собой двух тел равны по модулю и направлены по одной прямой в противоположные стороны. F12=-F21

4-й закон динамики (принцип независимости действия сил): ускорение сообщаемое м.т. равнодействующей силой равно геометрической сумме ускорений , которые получила бы точка от действия каждой из сил по отдельности.

2. 1-я и 2-я основные задачи динамики и методы их решения.

1-я задача (прямая): по известной массе точки и кинематическим характеристикам движения определяется действующая сила (решается дифференцированием кинематического уравнения движения)

2-я задача (обратная): по известным , массе точки , действующим силам и начальным условиям движения определить кинематические характеристики (решается интегрированием ДУ движения)

3. Дифференциальные уравнения движения точки в декартовых и естественных осях координат.

- ДУ движения несвободной м.т. в декартовых координатах

- главный вектор (геом. Сумма действующих на точку активных сил)

4.Дифференциальные уравнения движения несвободной материальной точки в форме Эйлера.

Если точка является несвободной (на движение точки наложены связи), в число действующих на точку сил включаются реакции связей.

Силы, входящие в правую часть дифференциальных уравнений движения, в общем случае могут являться функциями от времени t, скорости v и координат х, у, z точки.

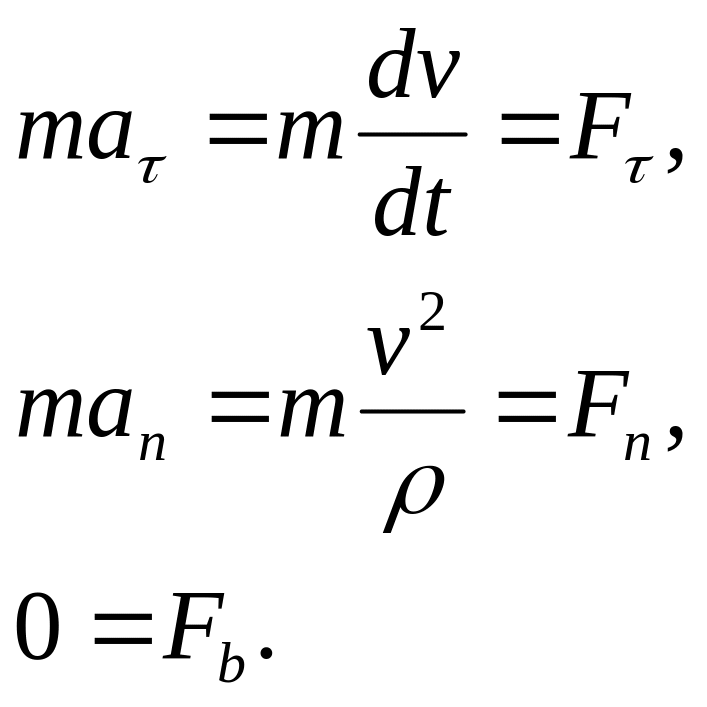- равнодействующая реакция связи

5.Прямолинейное движение материальной точки .

Равномерным прямолинейным движением называется движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения. Уравнение такого движения в векторной форме записывается так:

где  — перемещение,  — скорость движения, t — время.

При прямолинейном движении ось координат направлена по направлению движения точки , в результате чего из 3-х ДУ

остаётся одно:

6.Интегрирование ду движения в случаях , когда сила зависит от скорости, времени, координаты.

Интегрирование ДУ движения для случая F = F(t)

Уравнение задачи Коши с помощью первой подстановки a = dv/dt приводится к системе двух ДУ. получим первый интеграл – закон изменения скорости и второй интеграл – закон движения:

v = v₀ + (1/m) ,

x = x₀ +v₀t + (1/m) .

Интегрирование ДУ движения для случая F = F(x)

Уравнение задачи Коши с помощью второй подстановки a = vdv/dx позволяет получить первый интеграл

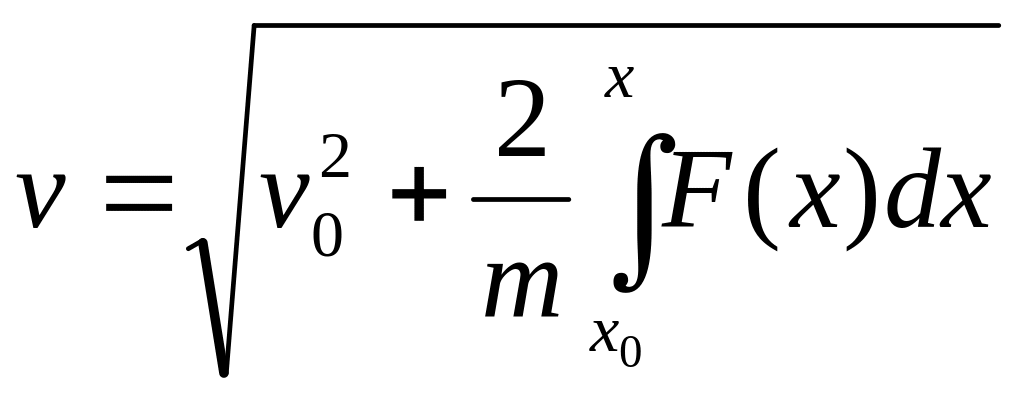
и второй – аналогичный :

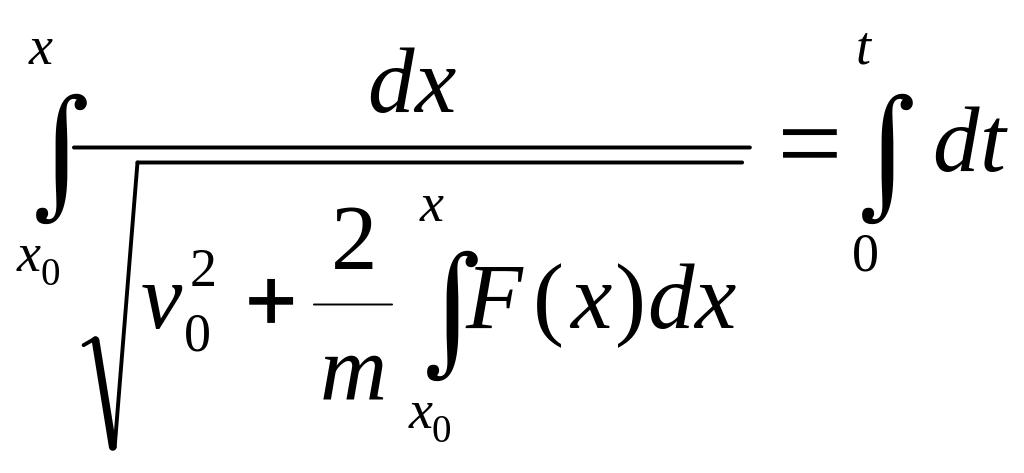
Интегрирование ДУ движения для случая F = F(v)

В этом случае рекомендуется пользоваться следующим правилом:

Если в задаче дано или нужно найти время t , применять первую подстановку a = dv/dt.

Если в задаче можно обойтись без определения времени, следует применять вторую подстановку a = vdv/dx.