Билет 8
1. Поясните термины: напряжённость магнитного поля, магнитное напряжение, скалярный магнитный потенциал, разность магнитных потенциалов, магнитодвижущая сила.
По определению напряжённость магнитного поля H [А/м] – векторная величина, полученная в данной точке путём вычитания намагниченности M от магнитной индукции B, делённой на магнитную постоянную : . В вакууме напряжённость магнитного поля во всех точках равна магнитной индукции, делённой на магнитную постоянную: . По аналогии с электрическим полем магнитное напряжение [А] – скалярная величина, равная линейному интегралу напряжённости магнитного поля H по направлению заданной линии, связывающей две точки A и B: .
Для
безвихревого (потенциального) магнитного
поля определен
скалярный
магнитный потенциал
[А], градиент которого, взятый со знаком
минус, равен напряжённости безвихревого
магнитного поля
.
Скалярный магнитный потенциал
неоднозначный, так как любая постоянная
скалярная величина может быть добавлена
к данному скалярному магнитному
потенциалу без изменения его градиента.
Разность
магнитных потенциалов
в точках B
и A
равна взятому со знаком минус линейному
интегралу напряжённости магнитного
поля по направлению любой линии,
связывающей эти точки
.
Магнитодвижущая
сила (МДС)
F
[А] — скалярный линейный интеграл по
направлению замкнутой линии от вектора
напряжённости магнитного поля
.
2. Методы расчетов силовых взаимодействий в магнитных системах интегрированием по источникам поля.
Модели
намагниченных деталей с кусочно-постоянным
распределением намагниченности (см.
п. 1.3.3.2)
по элементарным объемам можно рассматривать
как распределение поверхностных токов
или зарядов (рис.
1.42),
а силы, действующие на них, вычисляются
по известным формулам [8,
10].
Так совокупность N
элементарных объемов
, имеющих намагниченность
с
поверхностями
,
несущими распределенные токи плотностью
испытывает во внешнем магнитном поле
с магнитной индукцией
действие результирующей силы (ее по
аналогии с током в проводниках называют
силой Ампера)
, (10)
а
для той же совокупности объемов, применяя
модель с поверхностными магнитными
зарядами плотностью
,
во внешнем магнитном поле с напряженностью
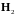по аналогии с электростатическим полем
можно использовать выражение силы
Кулона для распределенных зарядов
,
(11)
где
- внешние магнитная индукция и напряженность
магнитного поля ко всей рассматриваемой
совокупности объемов, т.е предполагается
что внутри совокупности взаимодействие
объемов скомпенсировано реакциями
механических связей.
Если
расчет опирается на дискретную модель
с объемными источниками – магнитными
токами
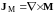или зарядами
,
то в формулах (10), (11) добавляются объемные
интегралы от ротора и дивергенции
намагниченности
;
. (12)
Алгоритм расчета предусматривает интегрирование функций по всем элементарным объемам и их поверхностям. Дискретный характер источников вносит дополнительные трудности, так как не позволяет уменьшить общее число узлов в квадратурной формуле. Увеличение точности возможно повышением степени дискретизации ферромагнитных элементов, что приводит к квадратичному возрастанию объема вычислений как на этапе расчета распределения намагниченности, так и на этапе расчета сил.