Билет 7

1. Поясните термины: магнитные диполи, магнитный момент, намагниченность, магнитная поляризация, напряжённость магнитного поля.

Магнитное поле создается токами, т.е. движущимися носителями зарядов. Малые замкнутые структуры микротоков в веществе представляют магнитными диполями — объектами, которые создают во всех точках пространства на расстояниях, достаточно больших по сравнению с его геометрическими размерами, такую же магнитную индукцию, как размещенный в нем плоский замкнутый виток тока. Его магнитный момент m [А·м²] —векторная величина, равная произведению тока, площади витка и единичного вектора, перпендикулярного к плоскости витка, направление которого соответствует ориентации витка (если смотреть по направлению вектора, то ток в витке должен протекать по направлению движения стрелок часов). Для совокупности магнитных диполей m – это сумма всех магнитных дипольных моментов элементарных магнитных диполей совокупности, т.е. объёмному интегралу намагниченности М: .

Намагниченность M [А/м] – это удельный параметр, равный магнитному дипольному моменту m совокупности магнитных диполей, содержащейся внутри малой области, делённому на ее объём V: . Намагниченность M удовлетворяет соотношению , где H – напряжённость магнитного поля. Векторная величина [Тл], называется магнитная поляризация.

По определению напряжённость магнитного поля H [А/м] – векторная величина, полученная в данной точке путём вычитания намагниченности M от магнитной индукции B, делённой на магнитную постоянную : . В вакууме напряжённость магнитного поля во всех точках равна магнитной индукции, делённой на магнитную постоянную: . По аналогии с электрическим полем магнитное напряжение [А] ­– скалярная величина, равная линейному интегралу напряжённости магнитного поля H по направлению заданной линии, связывающей две точки A и B: .

2. Расчет силовых взаимодействий в магнитных системах методом разделяющей поверхности.

Если имеются программные средства для расчетов электромагнитных полей, то для расчета сил в электромеханических системах применяют метод разделяющей поверхности [10]. Выделим в системе с помощью замкнутой поверхности ту деталь или группы деталей, на которую действует искомая сила (рис. 1.43). Суть метода ограничения области взаимодействия состоит в том, что отбрасывается одна из взаимодействующих частей МС, а ее влияние на напряженность поля учитывается введением поверхностных источников на разделяющей поверхности : зарядов и токов. Расчетная формула может быть получена из векторной формулы Грина для вектора напряженности магнитного поля с учетом того, что в немагнитном пространстве

, (13)

где — напряженность магнитного поля, созданная первой группой элементов. Нормальные и касательные составляющие H на в (13) дают вклад в поле такой, как простой слой зарядов и простой слой токов плотностью и соответственно. Следовательно, согласно (10), (11) искомая сила может быть вычислена по формуле

. (14)

Сила, действующая на со стороны первой группы элементов, равна по значению и противоположна по знаку силе, действующей на со стороны второй группы элементов, расположенной с внешней стороны . Если оставить направление нормали к такое же, как в (14), и повторить вывод во внешней области, для искомой силы можно записать подобное выражение

. (15)

Сложим почленно равенства (14) и (15). Учитывая, что 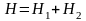, получаем

. (16)

Раскрыв в (16) двойное векторное произведение, получаем известную формулу Максвелла для пондеромоторной силы [8]

. (17)

У магнитных систем с малым немагнитным зазором между взаимодействующими деталями, например в электромагните клапанного типа, формула (17) может быть приближенно сведена к более простой , где — магнитный поток, проходящий между деталями в немагнитном зазоре через поперечное сечение трубки этого потока с площадью . Основные допущения: трубка потока линейная и имеет постоянное поперечное сечение; магнитная индукция по сечению трубки постоянна; сила направлена вдоль образующей трубки. Если взаимодействующие группы деталей имеют в немагнитном зазоре несколько таких трубок и другими магнитными потоками пренебрегаем, то результирующая сила будет равна векторной сумме сил всех трубок.