2. Расчет магнитных систем с учетом магнитного гистерезиса.

Отличительная особенность гистерезисных материалов, из которых изготавливаются постоянные магниты, — зависимость от предыстории намагничивания, т. е. принципиальная неоднозначность. Однако знание предыстории дает возможность выделить однозначные участки характеристики, на которых находятся искомые рабочие точки элементарных объемов деталей из гистерезисных материалов. Магнитные свойства таких материалов для модели магнитного поля необходимо представлять в трех пространственных координатах осей анизотропии (векторный гистерезис), так как они всегда имеют структурную или наведенную анизотропию свойств.

Упрощенное представление магнитного гистерезиса предполагает оперировать кривыми магнитного гистерезиса только в направлении оси легкого (основного) намагничивания . В двух других направлениях принимается линейная зависимость намагниченности от напряженности магнитного поля только своих компонент . Среди множества всех возможных состояний материала, задающих предысторию его намагничивания, с практической точки зрения для постоянных магнитов наиболее интересны три, которые связаны с технологией изготовления постоянных магнитов и магнитных систем:

1. Намагничивание постоянных магнитов производится в собранной магнитной системе до достижения намагниченности насыщения в направлении осей легкого намагничивания.

2. Постоянные магниты намагничиваются раздельно в уединенном состоянии до насыщения, а затем производится сборка магнитной системы.

3. Намагничивание собранной магнитной системы производится в условиях, требующих дополнительного анализа распределения поля.

Первое состояние постоянных магнитов однозначно определяется предельной кривой размагничивания (рис. 1.34а), при втором магниты будут работать на частных циклах, а для определения этих циклов требуется предварительный расчет магнита в уединенном состоянии по предельной кривой размагничивания, который дает точки отхода от нее частных циклов у каждого элементарного объема (рис. 1.34б). В третьем состоянии для определения характеристики каждого элементарного объема в размагничивающих полях необходим предварительный анализ процесса намагничивания постоянных магнитов в собранной системе, который должен быть построен на основе характеристик первоначального намагничивания (рис. 1.34в). Такой анализ позволяет определить точки отхода частных циклов от начальной кривой намагничивания и, далее, выполнить расчет по частным циклам.

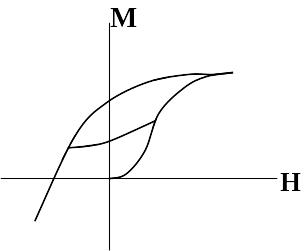
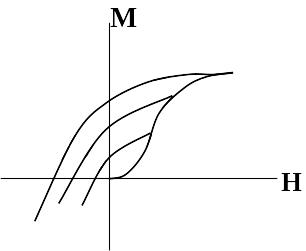
Билет 12

1. Поясните термины: магнитные материалы, абсолютная магнитная проницаемость, удельное магнитное сопротивление, относительная магнитная проницаемость, магнитная восприимчивость.

Магнитные материалы отличаются тем, что в магнитном поле в них возникает или изменяется намагниченность. Значения векторов магнитного поля в материале связывают магнитная проницаемость и магнитная восприимчивость. Абсолютная магнитная проницаемость 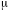[Гн/м] — скалярная величина, произведение которой на напряжённость магнитного поля в среде равно магнитной индукции: . Удельное магнитное сопротивление — обратная величина абсолютной проницаемости, если она существует. Относительная магнитная проницаемость равна абсолютной проницаемости , делённой на магнитную постоянную , т.е. . Магнитная восприимчивость — скалярная величина, произведение которой на напряжённость магнитного поля H равно намагниченности: . Также по определению напряженности магнитного поля векторы В, H и М связаны соотношением .

2. Система пространственных интегральных уравнений для векторов намагниченности ферромагнитных деталей магнитной системы со стационарным полем. Итерационный расчет намагниченности в деталях из магнитных материалов.

Рис. 1.26. Деталь магнитной системы: а – с непрерывным распределением намагниченности (плотности тока) по объему; б – с постоянным значением вектора намагниченности (плотности тока) во всем объеме; в – с кусочно-постоянной аппроксимацией вектора намагниченности (плотности тока) по объему

На рис. 1.26а приведено условное изображение детали магнитной системы в виде многогранника с непрерывными распределениями векторов намагниченности. Наиболее грубое приближение получаем при усреднении вектора по всему объему, т.е. при M=const (рис. 1.26б). В этом случае M=0 и для векторов поля справедливы выражения:

,

,

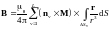где - площадь - й грани детали; – число граней.

Представить объемную картину распределения векторных источников дискретной моделью, асимптотически снижающей погрешности при уменьшении шага дискретизации (размера дискретного элемента), позволят кусочно-постоянная аппроксимация намагниченности по элементарным объемам , где - номер элементарного объема (рис. 1.26в). В этом случае интегрирование производится по всем поверхностям 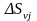, ограничивающим элементарные объемы.

,

,

где - номер элементарного объема; 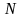-общее число выделенных элементарных объемов; - номер грани; 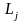- число граней -го элементарного объема; - площадь поверхности грани.

Эти формулы можно рассматривать как пространственные интегральные уравнения, если добавить к ним материальные уравнения среды — магнитные свойства материалов. Будем считать, что объем детали разбит на малых элементарных объемов, каждый из которых представляется многогранником с числом граней (рис. 1.26в). Деталь находится во внешнем магнитном поле. Выражение для напряженности поля запишем в виде

, (2)

где под 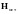понимается напряженность внешнего поля, создаваемого всеми остальными источниками поля магнитной системы. Помещая точку наблюдения последовательно в средние точки каждого выделенного элементарного объема, запишем равенств (2). В результате получим систему линейных алгебраических уравнений, связывающую неизвестные значения напряженности поля в элементарных объемах с искомыми значениями намагниченности. В матричной записи она имеет вид

, (3)

где многомерные векторы , и содержат компоненты векторов напряженности поля и намагниченности в каждом элементарном объеме. Матрица состоит из коэффициентов, которые определяются геометрической формой детали и способом разбиения на элементарные объемы (см. (2)).

Для поиска неизвестного распределения векторов намагниченности по элементарным объемам к системе уравнений (3) добавляют материальные уравнения — магнитные характеристики материала 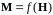и решают полученную систему уравнений.