25. Расчёт сил методом разделяющей поверхности

Если имеются программные средства для расчетов электромагнитных полей, то для расчета сил в электромеханических системах применяют метод разделяющей поверхности [10]. Выделим в системе с помощью замкнутой поверхности ту деталь или группы деталей, на которую действует искомая сила (рис. 1.43). Суть метода ограничения области взаимодействия состоит в том, что отбрасывается одна из взаимодействующих частей МС, а ее влияние на напряженность поля учитывается введением поверхностных источников на разделяющей поверхности : зарядов и токов. Расчетная формула может быть получена из векторной формулы Грина для вектора напряженности магнитного поля с учетом того, что в немагнитном пространстве

, (13)

где 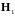— напряженность магнитного поля, созданная первой группой элементов. Нормальные и касательные составляющие H на в (13) дают вклад в поле такой, как простой слой зарядов и простой слой токов плотностью и 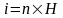соответственно. Следовательно, согласно (10), (11) искомая сила может быть вычислена по формуле

. (14)

Сила, действующая на со стороны первой группы элементов, равна по значению и противоположна по знаку силе, действующей на со стороны второй группы элементов, расположенной с внешней стороны . Если оставить направление нормали к такое же, как в (14), и повторить вывод во внешней области, для искомой силы можно записать подобное выражение

. (15)

Сложим почленно равенства (14) и (15). Учитывая, что , получаем

. (16)

Раскрыв в (16) двойное векторное произведение, получаем известную формулу Максвелла для пондеромоторной силы [8]

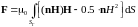. (17)

У магнитных систем с малым немагнитным зазором между взаимодействующими деталями, например в электромагните клапанного типа, формула (17) может быть приближенно сведена к более простой , где 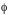— магнитный поток, проходящий между деталями в немагнитном зазоре через поперечное сечение трубки этого потока с площадью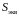 . Основные допущения: трубка потока линейная и имеет постоянное поперечное сечение; магнитная индукция по сечению трубки постоянна; сила направлена вдоль образующей трубки. Если взаимодействующие группы деталей имеют в немагнитном зазоре несколько таких трубок и другими магнитными потоками пренебрегаем, то результирующая сила будет равна векторной сумме сил всех трубок.

26. Квазистационарное магнитное поле

В электротехнических устройствах электромеханики обычно рассматриваются электромагнитные поля в квазистационарном приближении, когда можно пренебречь токами электрического смещения в вакууме. При этих условиях справедлива система уравнений Максвелла:

где в общем случае - сумма плотностей наведенного вихревого и стороннего тока; 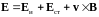- результирующий вектор напряженности электрического поля равный сумме индукционной и сторонней составляющих, а также составляющей от движения в магнитном поле; — полная производная вектора магнитной индукции (учитывает как изменение во времени источника, так и движение). Кроме того, в систему уравнений переменного электромагнитного поля входят уравнения непрерывности линий магнитной индукции и полного тока: ; .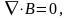

Для векторного магнитного потенциала в переменном поле с учетом принятых допущений справедливо аналогичное стационарному магнитному полю выражение

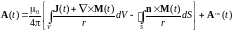, (4)

где - векторный потенциал, созданный сторонним током.

Вихрь напряженности электрического поля в соответствии с законом электромагнитной индукции определяется через векторный магнитный потенциал

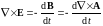
и поскольку при равенстве роторов векторов сами векторы равны с точностью до градиента скалярной функции, которую обозначим как электрический потенциал

. (5)

Истоком потенциальной составляющей при постоянной электрической проводимости  служит простой слой электрических зарядов с плотностью , наведенных на поверхностях электропроводящих деталей:

· (6)

Уравнения для расчетов источников переменного поля составляются из (4)-(6). Подставим (4) и (6) в (5) и умножим левую и правую части полученного равенства на электрическую проводимость среды, в которой находится точка наблюдения. Эти преобразования приводят к уравнению относительно распределенного в объеме проводника вихревого тока

, (7)

Чтобы рассчитать неизвестное распределение намагниченности в ферромагнитных и возможно электропроводящих деталях электромагнитного устройства, выразим магнитную индукцию через векторный магнитный потенциал и дополним полученное равенство магнитной характеристикой материала

. (8)

Уравнение для скалярного электрического заряда выводится подстановкой выражения для (5) в граничное условие нормальной компоненты nЕ=0 у поверхности проводника (линии тока касательные к поверхности проводника). Устремив точку наблюдения к поверхности со стороны проводника, с учетом предельных свойств интегрального оператора в выражении получаем граничное интегральное уравнение для определения 

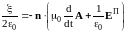. (9)