18. Уравнение для индуцированного тока.

Вихрь напряженности электрического поля в соответствии с законом электромагнитной индукции определяется через векторный магнитный потенциал

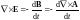
и поскольку при равенстве роторов векторов сами векторы равны с точностью до градиента скалярной функции, которую обозначим как электрический потенциал

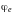
. (5)

Истоком потенциальной составляющей при постоянной электрической проводимости  служит простой слой электрических зарядов с плотностью , наведенных на поверхностях электропроводящих деталей:

· (6)

Уравнения для расчетов источников переменного поля составляются из (4)-(6). Подставим (4) и (6) в (5) и умножим левую и правую части полученного равенства на электрическую проводимость среды, в которой находится точка наблюдения. Эти преобразования приводят к уравнению относительно распределенного в объеме проводника вихревого тока

,

19. Стационарное магнитное поле. Ур-ния Максвелла

В стационарном электромагнитном поле имеются постоянные токи, но отсутствует электромагнитная индукция и 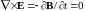. Система уравнений Максвелла включает также условие непрерывности линий магнитной индукции, закон полного тока и закон Ома:

,

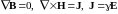где - объемная плотность токов; - электрическая проводимость среды.

Второе равенство — дифференциальная форма закона полного тока, указывает на существование, помимо потенциальной, вихревой составляющей у вектора напряженности стационарного магнитного поля. Истоки расположены внутри ферромагнитных элементов ( ), а его вихри — в проводниках с током ( ). У поля вектора магнитной индукции истоки отсутствуют ( ), а вихри располагаются в проводниках с током и в ферромагнитных элементах, так как

.

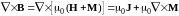Знания истоков и вихрей векторного поля во всем пространстве при условии отсутствия поля на бесконечности достаточно для определения самих векторов в любой точке

,

где для вычисления вихревой составляющей интегрирование производится по объему всех проводников с токами.

Поле вектора магнитной индукции только вихревое. Его определяют через векторный магнитный потенциал

.

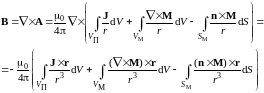Поэтому по аналогии с полем вектора магнитной индукции, созданного распределенными токами (см. первое слагаемое), намагниченные детали можно представить в виде магнитных токов (фиктивных):

- объемная плотность магнитных токов определена объемным ротором ; - поверхностная плотность магнитных токов определена поверхностным ротором .

20. Вектора намагниченности при стационарном поле.

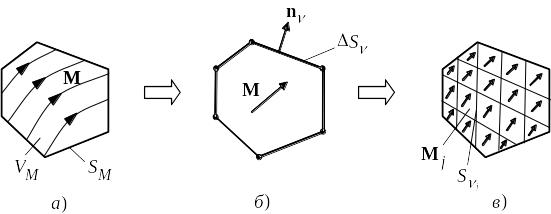
Рис. 1.26. Деталь магнитной системы: а – с непрерывным распределением намагниченности (плотности тока) по объему; б – с постоянным значением вектора намагниченности (плотности тока) во всем объеме; в – с кусочно-постоянной аппроксимацией вектора намагниченности (плотности тока) по объему

На рис. 1.26а приведено условное изображение детали магнитной системы в виде многогранника с непрерывными распределениями векторов намагниченности. Наиболее грубое приближение получаем при усреднении вектора по всему объему, т.е. при M=const (рис. 1.26б). В этом случае M=0 и для векторов поля справедливы выражения:

,

,

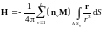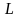где - площадь - й грани детали; – число граней.

Представить объемную картину распределения векторных источников дискретной моделью, асимптотически снижающей погрешности при уменьшении шага дискретизации (размера дискретного элемента), позволят кусочно-постоянная аппроксимация намагниченности по элементарным объемам , где - номер элементарного объема (рис. 1.26в). В этом случае интегрирование производится по всем поверхностям 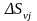, ограничивающим элементарные объемы.

,

,

где - номер элементарного объема; 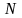-общее число выделенных элементарных объемов; - номер грани; 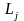- число граней -го элементарного объема; - площадь поверхности грани.

Эти формулы можно рассматривать как пространственные интегральные уравнения, если добавить к ним материальные уравнения среды — магнитные свойства материалов. Будем считать, что объем детали разбит на малых элементарных объемов, каждый из которых представляется многогранником с числом граней (рис. 1.26в). Деталь находится во внешнем магнитном поле. Выражение для напряженности поля запишем в виде

, (2)

где под 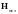понимается напряженность внешнего поля, создаваемого всеми остальными источниками поля магнитной системы. Помещая точку наблюдения последовательно в средние точки каждого выделенного элементарного объема, запишем равенств (2). В результате получим систему линейных алгебраических уравнений, связывающую неизвестные значения напряженности поля в элементарных объемах с искомыми значениями намагниченности. В матричной записи она имеет вид

, (3)

где многомерные векторы , и содержат компоненты векторов напряженности поля и намагниченности в каждом элементарном объеме. Матрица состоит из коэффициентов, которые определяются геометрической формой детали и способом разбиения на элементарные объемы (см. (2)).

Для поиска неизвестного распределения векторов намагниченности по элементарным объемам к системе уравнений (3) добавляют материальные уравнения — магнитные характеристики материала 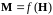и решают полученную систему уравнений.