1. Двойной интеграл

Если сущ Lim(n->бес, d->0) ,

не зависящей от вида кривых Гi и выбора точек

(пси I, эта i) то его наз-ют, двойным интегралом

от ф-ии F(x,y), по мн-ву и обозн-ют , где

эл-т площ-ди.

Св-ва. Аддитивность. Если квадрируемая область пр-на

Как обь-ие 2х обл-ей .

Линейность. Если ф-я f(x,y).g(x,y). Интегрируема на

И A,В э R то сущ.интеграл )dxdy=

dxdy+ dxdy

Если f(x,y), g(x,y) интег-ма на и f(x,y) ≤ g(x,y)

Люб (x.y) э , тто справедливо

dxdy≤ dxdy

Аналагично для модуля.

2) Сведение двойного интеграла к повторному.

Когда прямоугольник

Т1 пусть f(x,y) определена и интегрируема на прямоугольнике

П={[a,b]x[c,d]} и для люб Xэ[a,b]сущь тогда сущ

=

Разобьем прям-к на прям-ки с

Помощью прямых || осям координат

A=x₁,x₂…..x_n+1=b

C=y₁,y_2….y_l+1=a

Пij, i=1….n, j=1….l

Индекс соответствует номеру вершины

(ξ_i,𝜂_j)=П_ij

M_ij=inff(x,y),П_ij,M_ij=supf(x,y)

M_ij≤f(ξ,𝜂)≤mi

m_ij∆y_i≤ f(ξ,𝜂)∆yi≤ M_ij∆y_i

m_ij,∆y_i≤ M_ij∆y_i

Умножаем на ∆xi суммируем по i=1,n, j=1…l.

∆yi, ∆xi ≤ *∆xi≤ ∆y; ∆xi

S s

s-s-> 0 при n ->~ L->~

s= ∆xi≤s

Интегральная сумма для I(x) s->

Тогда ∆xi ->

т.о =

Док – во для прям уг – ка.

4) Замена переменных р\м dxdy

f(x,y) – обл св-ми а) f(x,y) – огр в . Б) Vɛ>0 люб эл-т ф-ии.

Элементарная функция содержащая все точки т линии

разрыва ф-ии f(x.y). сделаем разбиение соот-ие

разбиению . Пусть (xi,yi) э , тогда ɓ= ->

dxdy. Sni=(J(ξi^*, ηi^*) / *Sni по п(1). (ξi^*, ηi^*)э

Тогда ɓ= J(ξi^*, ηi^*)/ *Sn -> d->0

dξdη

Сущ- ие правых интегралов исходит из того f(x,y) обладает

Св- вом a,b в - квадрируема (как и ) получаем ф-лу

Замены переменных dxdy =

*/r

!Полярные координаты.

(r,φ)x=rcosф, y=rsinф

Экобиан перехода r=

J= = =rcos²ф+rsin²ф=r

dxdy= drdф

5)Тройной и n-кратный интегралы.с-ва.

Если сущь Lim(к->бес, d->0) не зависящий

от разбиений мн-ва G и выбора точек (Xⁱ₁,..Xⁱ_n), тогда этот

предел наз – ся n- кратным интегралом и обозначается

f(x₁,x₂,…x_n)dx_1….dx_n=

6)Сведение n-кратного интеграла к повторному.

G-кубическое мн-во. F-интегрируема на G. G – обл-ет св-м

Любая прям паралл оси Ox пересикает границу G не более

Чем в двух точках и проекции этих точек пересичение на Ox_i

Координат. А(x1.x2….x_i-1, x_i-1,…x_n­), B(x1.x2….x_i-1, x_i-1,…x_n­),

Пусть сущ dx_i=I(x1.x2….x_i-1, x_i-1,…x_n) и сущ (N-1)

I(x1.x2….x_i-1, x_i-1,…x_n) dx1.dx2….dx_i-1, dx_i-1,…dx_n

Где G’-Проекция G- на плоскость O(x1.x2….x_i-1, x_i-1,…x_n

7) Замена переменных в кратном интеграле

сос опред j= экобиан перехода

От x,y,z к u,v,w =

*Jdudvdw

8) !цилиндрические координаты. (r,ф,z)

j= = =

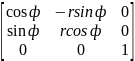rcos²ф+rsin²ф = r

Тогда =

R²=x²+y² ,r ≥0, 0≤ф≤2п

9) Сферические координаты(r,ф,θ)

r²=x²+y²+z² , п п/2, 0 2п,

j= = =

r²cos

10) кратные не собственные интегралы.опр.

Случай неотрицательной функции.

Пусть f(x) интегр по Vsn изменяеться исчерпывающей пл-ти.

Если сущ не зависящий от выбора пос-ти(𝛺_n)

То этот предел наз-ют кратным не собств интегр.

Тор неотриц ф Для того что бы от не отриц ф-ии сущ кратный

Несобств интеграл  сущ по одной из

Монотонности на исчерпывающей плоскости.

Док – во

(𝛺_n) – произвол плс-ть

I_n= , тк f(x) ≥ 0

𝛺_n+1…𝛺_n=> I_n+1≥I_n , (i_n) – монотонно возраст плоскость

Сущ limI_n (I_n) огран сверху. Пусть (Д_m) – упругая монотонная

Исчерпывающаяся плоскость. Сущь д_m: 𝛺_mпринадл Д_m

• I_n= ≤I_m­=>(I_n) опр=>

Сущ

11)

12) центр тяжести. Момент инерции. Потенциал

Момент инерции плоскости .

I₀ = - относительно начала координат

I₀ = - относительно осей OXOY

I₀ =

Центр тяжести

X₀=1/m

y₀=1/m

M=

Если Ύ(x,y) =1 то область однородна

13) Криволинейные интегралы первого рода по

плоской и пространственной кривой.

Существование и вычисление криволинейного интеграла

первого рода.

14)Свойства криволинейных интегралов первого рода

(линейность, аддитивность, оценка модуля, формула

среднего значения).

Линейность

Аддитивность если дуга AB состоит из двух частей ac и cb b

И если для f(x,y) сущ криволин интеграл 1рода по AB то для этой

ф-йй сущь криволин интеграл 1рода по по AC и CB и

оценка модуля сущ криволин интегр 1рода по AB от ф-ии f(x,y)

то сущ криволин интеграл от f v

формула среднего значения если f(x,y) непрерывна вдоль L=AB

то на AB найдется тМ

Где L длина кривой AB, L=

15)Криволинейные интегралы второго рода по плоской

и пространственной кривой. Существование и

вычисление криволинейного интеграла второго рода.

Пусть вдоль L=AB, определяеться непрерывная ф-ия

P(x.y), Q(x,y). вводя разбиение и расс-я те же точки m n

Составим две интеграл суммы

1- 𝛿₁= ∆x_n

2- ₂= ∆y_n

Где ∆x_n=x_n-x_n-1 и ∆y_{n =} y_n-y_n-1

Если сущ предел интеграл суммы 𝛿1(𝛿₂) при max |∆ln| ->0

То этот предел наз-ся криволин интеграл 2го рода и обозн

, (

Сущ + =

Общий криволин интеграл 2го рода

Сущ и выч интегр 2го рода

Если кривая L=AB явл-ся гладкой и не содержит особых точек

и если ф-ия p(x,y), Q(x,y) непрерывна вдоль этой кривой то

справедливы следующ ф-лы сводящие криволин интегр

2го рода к обычн опред

= ф’(t)dt

= ф’(t)dt