Билет №1.

1. Число а называется пределом последовательности { }, если для любого >0 , зависящий от , что для всех последующих n> имеет место

( n> |<

Необходимый признак существования предела последовательности : необходимо, чтобы она была ограничена.

Если последовательность имеет предел, то только один. (св- во пределов )

Теорема Больцано -Вейерштрасса : из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

2. a соответствует 1 и только 1 элемент b B, тогда говорят, что задано отображение А в В.

Если каждому образу b соответствует 1 и только 1 прообраз а, то такое отображение называется биекцией.

Если образу b соответствует не менее 1 прообраза, то такое отображение называется сюръекцией.

Если образу b соответствует не более 1 прообраза, то такое отображение называется инъекцией.

Билет № 2.

1. Число а называется пределом последовательности { }, если для любого >0 , зависящий от , что для всех последующих n> имеет место

( n> |<

Если последовательность имеет предел, то только один. (св- во пределов )

Теорема Больцано -Вейерштрасса : из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность.

2. Если множество М ограничено и сверху и снизу, то говорят, что оно ограничено.

( m < x< M)

Точные грани : 1) наименьшая из верхних границ называется точной верхней гранью. 2) наибольшая из всех нижних границ называется точной нижней гранью.

Теорема.

Всякое ограниченное сверху множество имеет точную верхнюю грань.

Всякое ограниченное снизу множество имеет точную нижнюю грань.

Билет № 3.

1. 1)Пусть переменной величине у по какому – либо правилу или закону поставлена в соответствие переменная величина х, тогда говорят, что задана функция у от аргумента х .

1.2)Определение 1 (по Коши) : Число А  называется пределом функции       в точке      , если для любого положительного числа         существует положительное число       такое, что для всех       , удовлетворяющих неравенству

,

выполняется неравенство

|f(x) – A| < .

В кванторах:

( (| |< ) : |f(x) – A| <

Определение 2( по Гейне) : Число  A называется пределом функции       в точке      , если для любой сходящейся к       последовательности { } соответствующая последовательность значений функции {f( )} сходится к числу  A.

1.3)Единственность предела функции в точке : если функция f(x) имеет в точке предел, то только один. (св-во пределов функций).

1.4) При приближении к точке слева предел функции f(x) в точке = А , а при движении справа предел функции в точке = В.

Принято число А называть левосторонним пределом, а число В - правосторонним пределом.

Если А В, то общего предела в точке не существует.

Таким образом, чтобы в точке существовал предел необходимо, чтобы существовали односторонние пределы ( лево- и правосторонние пределы) и были равны друг другу.

2. 1) строится приращение функции f(x)

2) строится и упрощается

3) вычисляется при x 0 = f΄( )

Билет № 4.

1. Функция f(x) называется непрерывной в точке ,если в этой точке существует предел, и он равен значению функции в этой точке.

( >0) ( | < : |f(x) – f( | <

Если функция f(x) непрерывна в каждой точке интервала [a, b], то функция f(x) называется непрерывной на этом интервале.

2. Если предел в точке отсутствует или существует, но не равен значению функции в этой точке , то говорят, что функция f(x) «разрывна» в точке или «терпит разрыв» в точке

Точка х₀ называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы.

Точка х₀ называется точкой разрыва 2 – го рода, если в этой точке хотя бы один из односторонних пределов бесконечен.

Если значения на берегах разрыва разные, то значение функции в точке может быть любым (или вообще отсутствовать), всё равно будет давать разрыв первого рода. Если же значения на берегах разрыва совпадают, то для наличия разрыва нужно, чтобы либо эти совпадающие значения были отличны от значения функции в точке , либо функция в этой точке была вовсе не определена. Если в этом случае переопределить (или доопределить) функцию в точке , положив , то полученная изменённая функция будет уже непрерывна в точке и разрыв в точке исчезнет; отсюда и название такого разрыва -- устранимый.

3. 1) если функции f(x) и g(x) являются непрерывными в точке ,то их сумма, разность, произведение и частное (кроме 0- знаменатель) также есть непрерывные функции в точке

4. 2) f(x) , x= ,тогда говорят, что задана композиция функций f и .

Другими словами, это сложная функция. Если f(x) непрерывны в соответствующих областях, то их композиция также непрерывна.

2. Производная сложной функции :

(f(g(x)))΄ = f΄(g(x)) g΄(x)

Производная параметрически заданной функции :

Y=y(t) ,

X=x(t)

=

Билет № 5.

1. Пусть функция f(x) определена и непрерывна в некоторой окрестности точки ,тогда если существует конечный предел ( ), то он называется производной функции f(x) в точке .

Физический( механический) смысл производной : если f(x) есть какой – либо процессЮ то производная от f(x) есть скорость изменения этой функции f(x).

Геометрический смысл производной : производной функции f(x) в точке численно равна tg угла наклона касательной к графику f(x) в точке .

Правила дифференцирования :

1) (u+v) =u +v

2) (uv) =u v+uv

3)( )΄ =

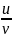Производная обратной функции :

Пусть у(х) имеет обратную функцию (х) = х(у).

Функция у(х) называется обратимой, (х)=х(у) – обратной

2. Функции , которые могут быть получены из основных элементарных функций посредством арифметических действий и образования сложных функций, называются элементарными функциями.

Элементарные функции :

1. Трансцендентные

2. Алгебраические

а) рациональные

б) иррациональные

3) целые рациональные

4) дробные рациональные

Билет № 6.

1. Y=arcsin x

-

Область определения : [-1;1]

Область значений : [-

Четность, нечетность : нечетная

Нули : у=0 при х=0

Промежутки знакопостоянства : у< 0 при х [-1;0)

y>0 при х (0;

Экстремумы : нет

Промежутки монотонности : возрастает на всей области определения

Y=sin x

Область определения: D(f ) = R .

Область значений: E(f ) = [-1;1].

Периодичность: периодическая с основным (наименьшим положительным) периодом 2

Четность и нечетность: sin x - нечетная функция;

Интервалы монотонности:

sin x возрастает при х (- , n Z;

убывает при х ( n) , n Z

Экстремумы : max sin x =1 и достигается в точках х = , n Z

Min sin x = -1 в точках х= - , n Z

2. Функция y=f(x) называется бесконечно малой при x→a или при x→∞, если или , т.е. бесконечно малая функция – это функция, предел которой в данной точке равен нулю.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Теорема 4 (свойства бесконечно малых функций).

1. Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2. Произведение бесконечно малой функции на ограниченную функцию есть бесконечно малая.

3. Произведение конечного числа бесконечно малых является бесконечно малой.

Определение 9 (бесконечно большая функция). Функция называется бесконечно большой при x a или в точке a, если для любого положительного числа  найдется такое положительное (), что для всех x a и удовлетворяющих условию |x-a|< будет выполнено неравенство |f(x)|> .

Теорема 1. Если функция f(x) является бесконечно большой при x→a, то функция 1/f(x) является бесконечно малой при x→a.

Теорема 2. Если функция f(x) - бесконечно малая при x→a (или x→∞) и не обращается в нуль, то y=1/f(x) является бесконечно большой функцией.

Билет № 7.

1. Y= ln f(x) –логарифмическая функция

Y=ln t, t= f(x), тогда по формуле производной сложной функции имеем :

= f

F(x) =

Для вычисления производной прологарифмируем :

Ln f(x) =v(x) ln u(x)

Продифференцируем :