29. Сведение матричной игры к задачам линейного программирования. Приведите примеры.

Ответ: Пусть игрок А обладает матричными стратегиями А₁,…,A_m, игрок В – B₁,…,B_n. При этом платежная матрица имеет вид P=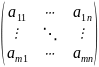 . Необходимо определить оптимальные стратегии для игрока А – S_A*=(p₁*,…,p_m*), и для игрока В – S_B=(q₁,…,q_n). При этом 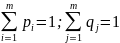. Оптимальная стратегия S_A* обеспечивает игроку А средний выигрыш, не меньший чем цена игры ν при любой стратегии игрока В и выигрыш, равный в цене ν, при оптимальной стратегии игрока В.

Для оптимальной стратегии S_A* все средние выигрыши должны быть не меньше цены игры ν:

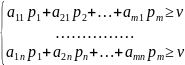
Пусть . Поделим систему на

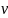
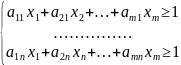
Цель А – максимизировать выигрыш: νmax. 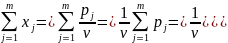min

Получена ЗЛП f=x₁+…+x_m с ограничениями

Для определения оптимальной стратегии игрока В необходимо учесть, что он стремится минимизировать выигрыш А: νmin. ЗЛП: φ=y₁+…+y_mmax при тех же ограничениях

30. Матричная игра и взаимно двойственные задачи линейного программирования. Приведите примеры.

Ответ:

31. Принятие решений в условиях полной неопределенности. Критерии Вальда ,Сэвиджа, Гурвица, Лапласа.

Ответ: Для принятия решений в условиях полной неопределенности существуют 4 критерия:

1) Критерий Вальда (принцип наибольшей осторожности) – оптимальной будет та стратегия, для которой достигается значение W=

2) Критерий Сэвиджа (крайнего пессимизма) – оптимальной считается та стратегия, для которой минимизируется максимальный риск

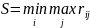
3) Критерий Гурвица – оптимальна стратегия, при которой достигается значение

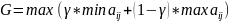
4) Критерий Лапласа – все вероятности состояния природы П_о полагаются равными q_j=1/n. Оптимальна стратегия, при которой достигается значение L=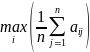

32. Постановка задачи динамического программирования. Состояния системы. Управление. Уравнение состояний. Поясните смысл отсутствия последействия в динамической системе.

Ответ: Рассмотрим динамическую систему, которая последовательно, за n

шагов, переходит из некоторого начального состояния s₀ в конечное состояние s_n. Промежуточные состояния s_i определяют состояния системы после i-ого шага. Как правило, состояния системы характеризуются несколькими числами, поэтому предполагается, что s_i являются векторами с m координатами, т.е. s_i=(s_i¹,…, s_i^m). Переход системы из состояния s_i-1 в состояние s_i определяется параметрами (управления) u₁ (i=1,…,n) при помощи уравнений состояний s_i=F_i(s_i-1,u_i), а эффективность каждого шага оценивается функциями f_i(s_i-1,u_i). Таким образом, эффективность всего процесса характеризуется суммой z­₀=f₁(s₀,u₁)+f₂(s₁,u₂)+…+f_n(s_n-1,u_n), а задача состоит в том, чтобы выбрать набор управлений u₁,…,u_n­, оптимизирующий z₀: z₀*=z₀*(s₀)=max z₀

Процесс решения разбивается на n шагов, для этого введем функцию

z_i(s_i)=f_i+1(s_i,u_i+1)+…+f_n(s_n-1,u_n), i=1,…,n-1, которая характеризует эффективность перехода от состояния s_i к s_n. Последовательно оптимизируя z_n-1(s_n-1),…,z₀(s₀) по формулам

z*_n-1(s_n-1)=maxf_n(s_n-1,u_n)

z*_n-2(s_n-2)=max(f_n-1(s_n-2,u_n-1)+z*_n-1(s_n-1))

… … … … …

z*₀(s₀)=max(f₁(s₀,u₁)+z₁*(s₁))

находим оптимальное решение задачи. Как видим, процесс решения задачи начинается с оптимизации последнего шага, что называется обратным ходом вычислений и свойственно многим задачам динамического программирования.