18. Постановка задачи целочисленного программирования. Примеры задач с экономическим содержанием.

Ответ: Основным отличием постановки задачи целочисленного программирования от задачи линейного программирования является то, что значения переменных, составляющих оптимальное решение задачи целочисленного программирования, должны быть целыми неотрицательными числами.

Итак, требуется найти минимальное (максимальное) значение

линейной функции 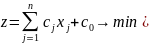) при линейных ограничениях 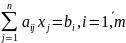а также при условии неотрицательности и целочисленности переменных: x_j≥0, x_j∈X, j=1,…,n.

19. Общая постановка задач многокритериальной оптимизации. Примеры задач с экономическим содержанием.

Ответ: Задача многокритериальной оптимизации похожа на стандартную задачу линейного программирования, единственное отличие состоит в том, что в этих задачах 2 и более целевых функций. Например,

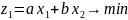
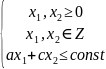
20. Что называется оценкой допустимого решения задачи многокритериальной оптимизации? Как определяется отношение строгого предпочтения на множестве допустимых решений D? Приведите примеры несравнимых элементов из D.

Ответ: Оценка допустимого решения многокритериальной задачи оптимизации – это вектор вида f(x)=(f₁(x),…,f_n(x)), где f₁,…,f_n – целевые функции.

Говорят, что x строго предпочтительнее y, если решение x превосходит или равно решение y по всем критериям, то есть, выполняется неравенство f_i(x)≥f_i(y) для всех i=1,…,n

21. Дайте определения доминирования по Парето. Приведите примеры. Эффективное (недоминируемое) решение.

Ответ: Отношение доминирования, введенное на множестве допустимых решений, называется доминированием по Парето (Пример: (5,10) и (10,5); f₁=4x₁+10x₂; f₂=x₁+x­₂; f(5,10)=(120,15), f(10,5)=(90,15) => (5,10) доминирует (10,5)

Допустимое решение из множества D называется эффективным, если не существует решений y, для которых не выполняется одно из условий: 1) f_i(y)≥f_i(x); 2) Ǝj такое что f_j(y)>f_j(x). Эффективное решение называется также оптимальным по Парето.

22. Дайте определение Парето-эффективной границы и приведите пример ее построения. Ответ: Множество Парето-оптимальных решений называется Парето-оптимальной границей.

Для задачи вида

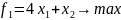
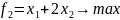
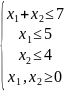Парето-оптимальной границей будет отрезок BC.

23. Основные методы решения задач многокритериальной оптимизации.

Ответ: 4 метода:

1) Метод субоптимизации – выделяется один из критериев, а по всем остальным критериям назначаются нижние границы

2) Лексико-графическая оптимизация (метод оптимизации) – упорядоченное множество критериев по их важности. На 1-м шаге выбирают самый важный критерий и по нему решают задачу оптимизации. Если получено одно решение, то оно и является оптимальным, если несколько – выбирают второй по значимости критерий и вновь решают задачу оптимизации и т.д.

3) метод обобщенного критерия – обобщенным критерием называется взвешенная сумма f=α₁f₁+…+α_nf_n, где α₁,…,α_n – веса, которые выбираются самостоятельно, сумма которых равна 1, т.е.